Attention » Attention(七)——RWKV, RoPE, BERT进阶(1)
2020-12-23 :: 7284 WordsState Space Model
Mamba(续)
因此Mamba参考FlashAttention,设计了分块增量的卷积算法应对这个问题,也就是所谓的parallel scan。
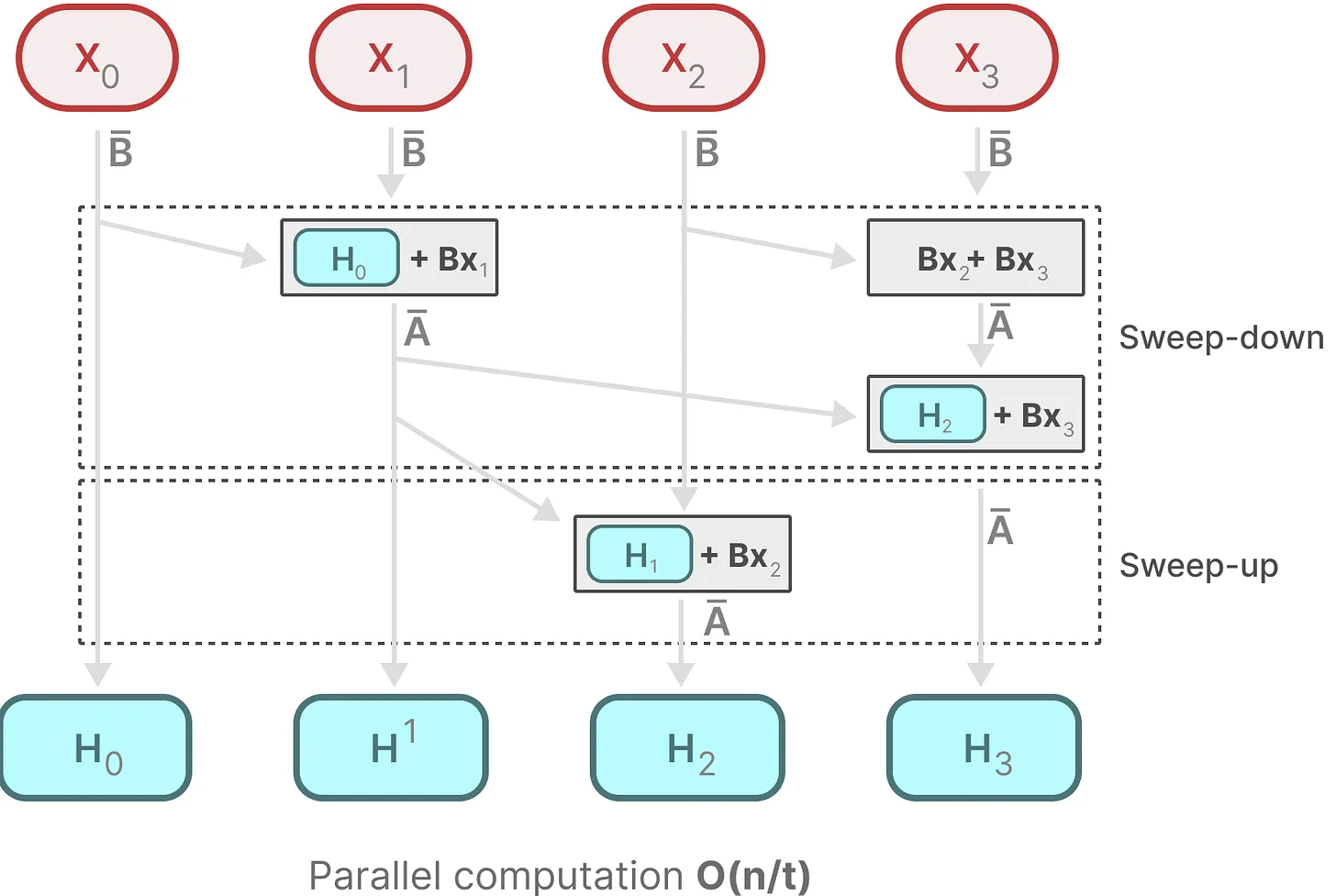
上图是parallel scan的示意图,虽然计算N时刻的B,需要依赖N-1时刻的B,但是上文部分和本文部分的计算可以是并行的,两部分都做完之后,综合之,即可得到最终结果。
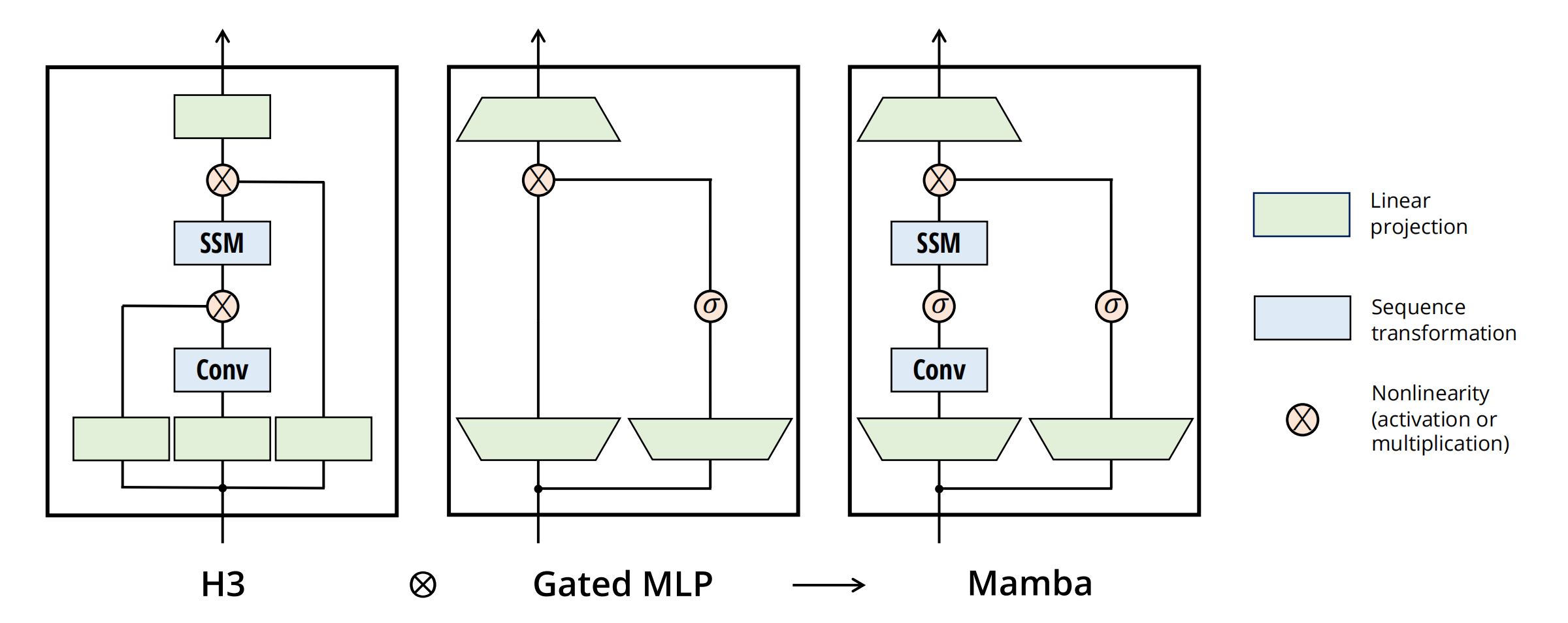
最终的Mamba Block如上图所示。其中的H3(Hungry Hungry Hippos)是之前提出的一种SSM架构。
transformer中的FFN+GLU,被Conv取代,位置也有调整。

https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-mamba-and-state
A Visual Guide to Mamba and State Space Models
https://blog.csdn.net/v_JULY_v/article/details/134923301
一文通透想颠覆Transformer的Mamba:从SSM、HiPPO、S4到Mamba
https://blog.csdn.net/v_JULY_v/article/details/140131413
一文通透mamba2:力证Transformer are SSM——从SSM、半可分矩阵、SSD到mamba2
https://blog.csdn.net/v_JULY_v/article/details/144317440
一文速览mamba的各种变体与改进:从MoE-Mamba、Vision Mamba、VMamba、Jamba到Falcon Mamba
RWKV
Linear Transformer

Linear Transformer将QKV的左乘变成右乘,从⽽将理论计算复杂度降为线性。在一般的NLP任务中,一个Head d的特征维度总是比输入序列长度N小得多的。
Linear Transformer使用如下方式取代softmax,来进行相似度计算。
\[\begin{equation}\text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j) = \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)\label{eq:gen-att-2}\end{equation}\]其中,\(\phi(\cdot),\varphi(\cdot)\)是值域非负的激活函数。
https://spaces.ac.cn/archives/7546
线性Attention的探索:Attention必须有个Softmax吗?
https://mp.weixin.qq.com/s/loNPfwHlBJ0CXIAya_vy3w
谈谈未来Attention算法的选择, Full, Sparse or Linear?
Attention free transformer
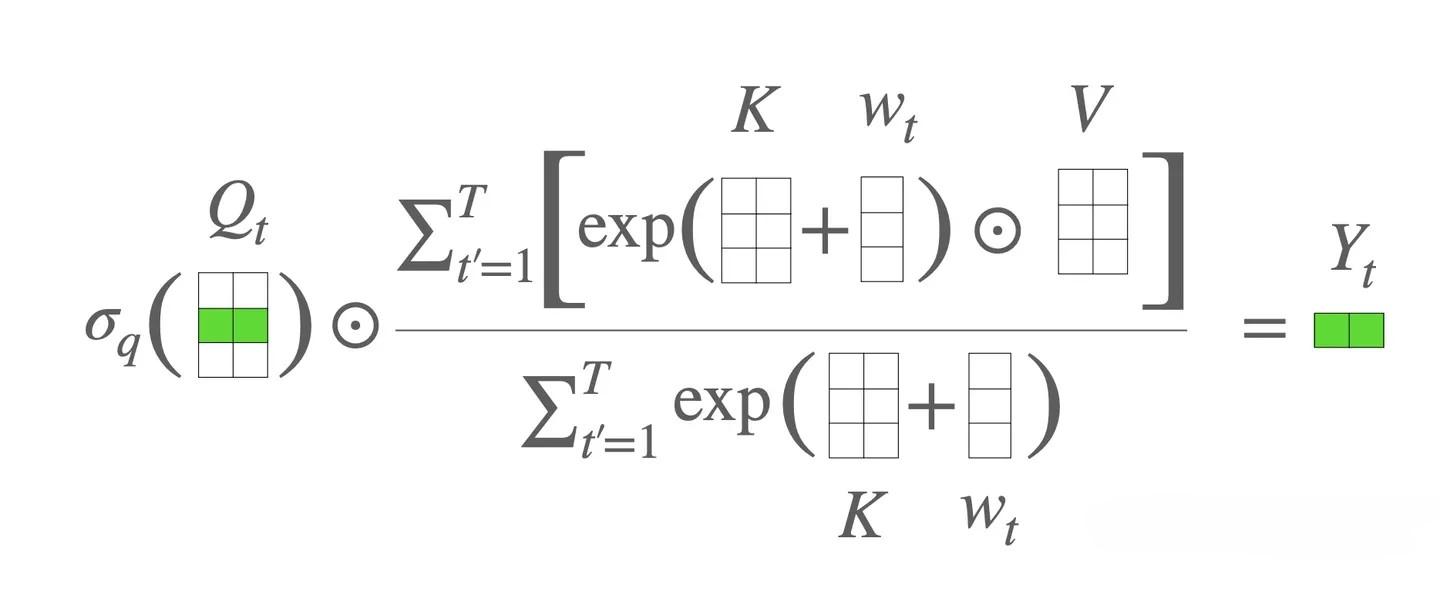
https://www.cnblogs.com/tuyuge/p/17407771.html
Attention free transformer
RWKV
代码:
https://github.com/BlinkDL/ChatRWKV
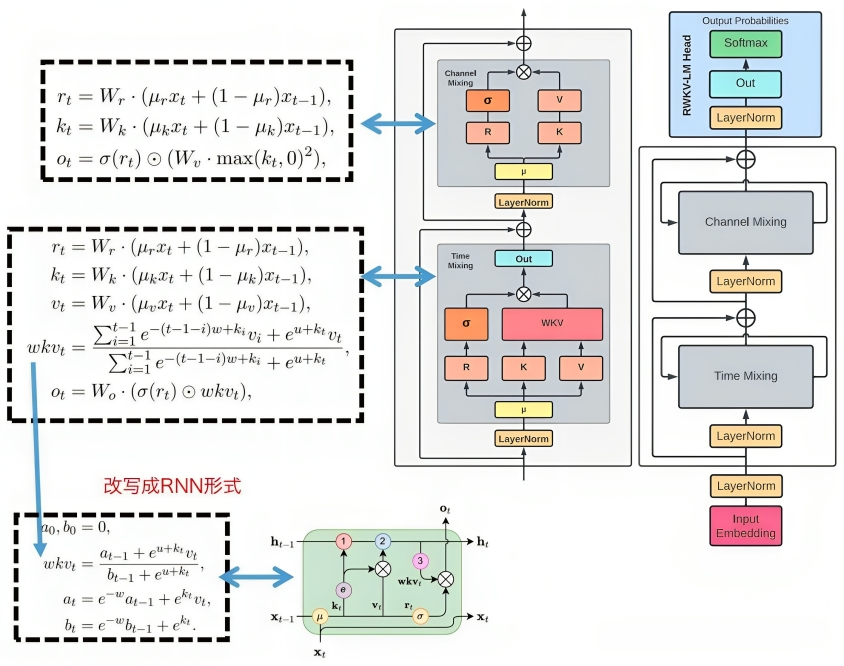

RWKV训练的时候用主图的CNN形式,而推理的时候用左下角的RNN形式。
RNN的weight不随输入序列的不同而不同,而RWKV会根据输入序列,计算得到weight,这个weight随输入序列的变化而变化的特性,正好是attention的特性。
RWKV没有使用attention,而是号称100%RNN。
Q:RNN-based没有attention之类机制的模型是怎么获得long memory的能力的啊?
A:这个形式就是Transformers are RNNs的形式,只不过把Q换成了positional invariant的time weighting。最近很多work都显示Attention里的Q其实没啥用,换成一个跟着相对位置exponential decay的term就行了。
参考:
https://zhuanlan.zhihu.com/p/605425639
RWKV 14B对比GLM 130B和NeoX 20B,展示RWKV的性能
flash-linear-attention
由杨松琳提出的类mamba算法。
https://sustcsonglin.github.io/blog/2024/deltanet-1/
DeltaNet Explained
代码:
http://github.com/fla-org/flash-linear-attention
RoPE
Embedding
预训练刚兴起时,在语言模型的输出端重用Embedding权重是很常见的操作,比如BERT、第一版的T5、早期的GPT,都使用了这个操作,这是因为当模型主干部分不大且词表很大时,Embedding层的参数量很可观,如果输出端再新增一个独立的同样大小的权重矩阵的话,会导致显存消耗的激增。不过随着模型参数规模的增大,Embedding层的占比相对变小了,加之《Rethinking embedding coupling in pre-trained language models》等研究表明共享Embedding可能会有些负面影响,所以现在共享Embedding的做法已经越来越少了。
https://kexue.fm/archives/9698
语言模型输出端共享Embedding的重新探索
外推性
对于Transformer模型来说,其长度的外推性是我们一直在追求的良好性质,它是指我们在短序列上训练的模型,能否不用微调地用到长序列上并依然保持不错的效果。
自从Transform被提出以来,一个基本问题还没有被解决,一个模型如何在推断时对训练期间没有见过的更长序列进行外推。众所周知,Bert支持的最长句子长度是512,那为什么Bert只能支持512的句子长度呢?
我们看一下BertEmbeddings的初始化,我们可以看到position_ids,被初始化成0-511,这个也就是BERT处理文本最大长度是512的原因,这里Bert使用的是绝对位置编码。
参考:
https://spaces.ac.cn/archives/9431
长度外推性与局部注意力
https://zhuanlan.zhihu.com/p/656684326
大模型位置编码-ALiBi位置编码
RoPE
Rotary Position Embedding是苏剑林的作品,并被后来流行的LLAMA等大模型所采用。DeepSeek的实验显示ALiBi明显不如RoPE。
RoPE采用绝对位置编码的形式实现相对位置编码,即寻找满足下式的g:
\[<f_{q}\left(x_{m}, m\right), f_{k}\left(x_{n}, n\right)>=g\left(x_{m}, x_{n}, m-n\right)\]其中的m和n是位置,x是未添加Position Embedding的原始词向量。上式左侧的内积运算,实际上就是Attention中的QK内积。
最终找到的g的公式(d=2)如下:
\[g\left(\boldsymbol{x}_{m}, \boldsymbol{x}_{n}, m-n\right)=\left(\begin{array}{ll} \boldsymbol{q}_{m}^{(1)} & \boldsymbol{q}_{m}^{(2)} \end{array}\right)\left(\begin{array}{cc} \cos ((m-n) \theta) & -\sin ((m-n) \theta) \\ \sin ((m-n) \theta) & \cos ((m-n) \theta) \end{array}\right)\left(\begin{array}{c} k_{n}^{(1)} \\ k_{n}^{(2)} \end{array}\right)\]也可以扩展到更高维度:
\[\boldsymbol{R}_{\Theta, m}^{d}=\underbrace{\left(\begin{array}{ccccccc} \cos m \theta_{0} & -\sin m \theta_{0} & 0 & 0 & \cdots & 0 & 0 \\ \sin m \theta_{0} & \cos m \theta_{0} & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m \theta_{1} & -\sin m \theta_{1} & \cdots & 0 & 0 \\ 0 & 0 & \sin m \theta_{1} & \cos m \theta_{1} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d / 2-1} & -\sin m \theta_{d / 2-1} \\ 0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d / 2-1} & \cos m \theta_{d / 2-1} \end{array}\right)}_{\boldsymbol{W}_{m}}\] \[\theta_i = 10000^{-2i/d}\]考虑到上述形式和欧拉公式以及复数的关系,这实际上就是一个如下图所示的旋转变换:
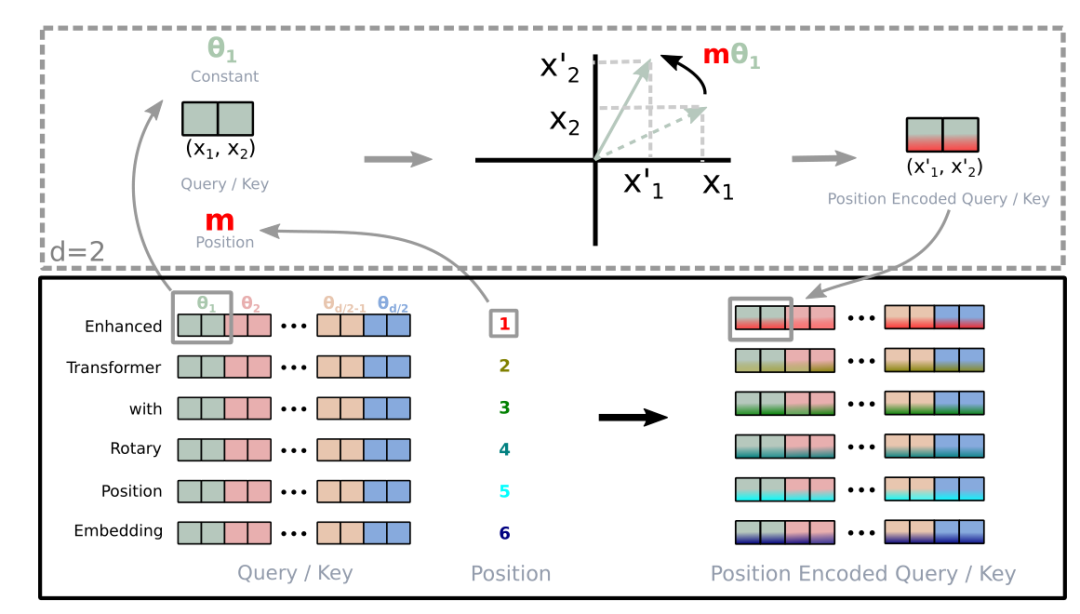

目前业界对于Rope的实现有两种方式:
- GPT-J sytle:原始论文的实现方式。
- GPT-NeoX style:该方式实现高效,为目前主流的LLM模型所使用。
两种实现方式在模型的表达能力上是等价的:\(Q*K^T\)的运算满足内积线性叠加性,即对于Q的行和K的列到底在哪里不关心,只要能把正确的行和列匹配上即可。
因此虽然对于同一input tensor x,rope_gpt_j(x) != rope_gpt_neox(x)。但是我们可以通过对\(W_Q\)和\(W_K\)重排,得到相同的\(Q*K^T\)的结果。
参考:
https://spaces.ac.cn/archives/8265
博采众长的旋转式位置编码
https://blog.csdn.net/v_JULY_v/article/details/134085503
一文通透位置编码:从标准位置编码、旋转位置编码RoPE到ALiBi、LLaMA 2 Long
RoPE的外推

两种常见的外推方法:

PI:Position Interpolation,形象的说就是增加线上点的密度。
ABF:Adjusted Base Frequency,增加base旋转的角密度。
https://blog.csdn.net/v_JULY_v/article/details/135072211
大模型长度扩展综述:从直接外推ALiBi、插值PI、NTK-aware插值、YaRN到S2-Attention
https://blog.csdn.net/v_JULY_v/article/details/137955982
一文速览Llama 3及其微调:从如何把长度扩展到100万到如何微调Llama3 8B
BERT进阶
UniLM
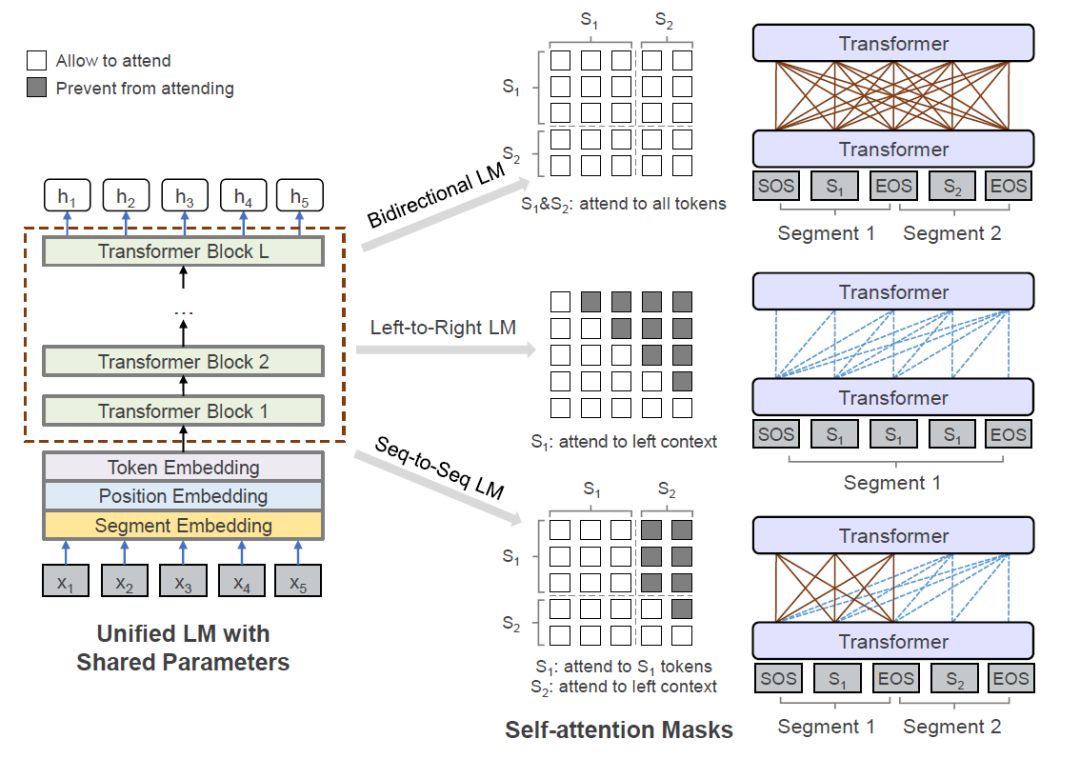
| Encoder注意力 | Decoder注意力 | 是否共享参数 | |
|---|---|---|---|
| GPT | 单向 | 单向 | 是 |
| UniLM | 双向 | 单向 | 是 |
| T5 | 双向 | 单向 | 否 |
https://mp.weixin.qq.com/s/m_FU4NmjUsvxusRidDb-Xg
UniLM:一种既能阅读又能自动生成的预训练模型
https://mp.weixin.qq.com/s/yyUPqxpfBwUSRbwM6SSAcQ
UniLM论文阅读笔记
https://mp.weixin.qq.com/s/RjeuHXa8O3MzSpTOuOHMkQ
站在BERT肩膀上的NLP新秀们:XLMs、MASS和UNILM
https://mp.weixin.qq.com/s/UEBKSKEkZTbpR49_Rh50Jg
微软统一预训练语言模型UniLM 2.0解读
Electra
https://mp.weixin.qq.com/s/dFT7KKMH56unkOEA9H4Kuw
吊打BERT Large的小型预训练模型ELECTRA终于开源!真相却让人…
https://mp.weixin.qq.com/s/6i9eQISKsWU0jawKzWg8nQ
超越bert,最新预训练模型ELECTRA论文阅读笔记
https://mp.weixin.qq.com/s/lkB1xn6G2P5Nivj7DcYg5w
Electra: 判别还是生成,这是一个选择

您的打赏,是对我的鼓励
