• Vanilla Attention
  • Luong Attention and Bahdanau Attention
• Neural Turing Machines
  • Attentional Interfaces
  • Adaptive Computation Time
• 花式Attention
  • Scaled Dot-Product Attention

Vanilla Attention

众所周知，RNN在处理长距离依赖关系时会出现问题。理论上，LSTM这类结构能够处理这个问题，但在实践中，长距离依赖关系仍旧是个问题。例如，研究人员发现将原文倒序（将其倒序输入编码器）产生了显著改善的结果，因为从解码器到编码器对应部分的路径被缩短了。同样，两次输入同一个序列似乎也有助于网络更好地记忆。

倒序句子这种方法属于“hack”手段。它属于被实践证明有效的方法，而不是有理论依据的解决方法。

大多数翻译的基准都是用法语、德语等语种，它们和英语非常相似（即使汉语的词序与英语也极其相似）。但是有些语种（像日语）句子的最后一个词语在英语译文中对第一个词语有高度预言性。那么，倒序输入将使得结果更糟糕。

还有其它办法吗？那就是Attention机制。

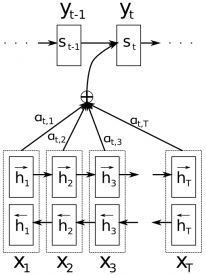
上图是Attention机制的结构图。y是编码器生成的译文词语，x是原文的词语。上图使用了双向递归网络，但这并不是重点，你先忽略反向的路径吧。重点在于现在每个解码器输出的词语\(y_t\)取决于所有输入状态的一个权重组合，而不只是最后一个状态。a是决定每个输入状态对输出状态的权重贡献。因此，如果\(a_{3,2}\)的值很大，这意味着解码器在生成译文的第三个词语时，会更关注于原文句子的第二个状态。a求和的结果通常归一化到1（因此它是输入状态的一个分布）。

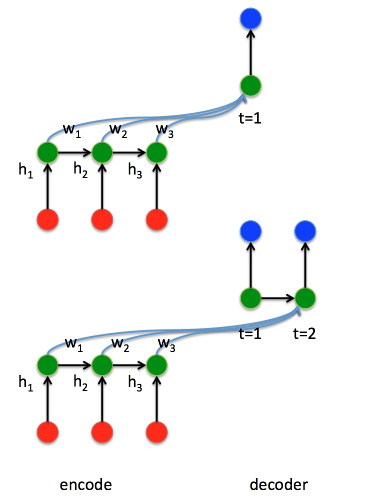
上图是添加了Attention机制之后的seq2seq的框架图。

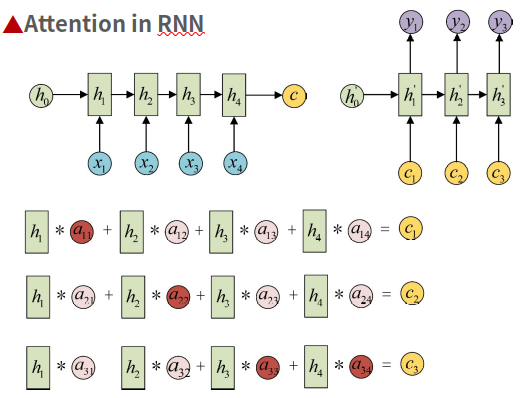
需要注意的是，在通常的使用中，W的值不仅和位置有关，还和时间有关。因此，上图中的W的值在Step 1和Step 2中是不同的。（上上图中，\(a_{t,2}\)的t也表明了这一点。）假设输入语句长度为M，输出语句长度为N，词向量的长度D，则W是一个\(M\times N\times D\)的tensor。

如果不考虑时间问题，那么Attention就退化为普通的FC，这时的W就是一个\(M\times D\)的tensor了。因此，Attention的参数量比普通的FC要大的多。

这里有一个训练的小技巧。虽然输出语句的长度不能事先得知，但不妨设置一个最大值\(N_{max}\)，这样tensor的尺寸就可以定下来了。然后用mask技术挡住后面的输出词语即可。例如我们训练生成第i个词的权重时，前面的i-1个词的mask为1，而后面的其他词的mask为0。

Attention机制的一个主要优势是能够解释并可视化整个模型。举个例子，通过对attention权重矩阵a的可视化，我们能够理解模型翻译的过程。

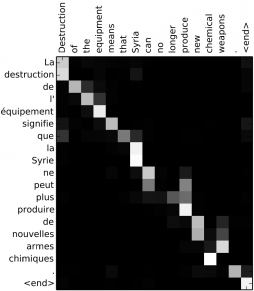
我们注意到当从法语译为英语时，网络模型顺序地关注每个输入状态，但有时输出一个词语时会关注两个原文的词语，比如将“la Syrie”翻译为“Syria”。

如果再仔细观察attention的等式，我们会发现attention机制有一定的成本。我们需要为每个输入输出组合分别计算attention值。50个单词的输入序列和50个单词的输出序列需要计算2500个attention值。这还不算太糟糕，但如果你做字符级别的计算，而且字符序列长达几百个字符，那么attention机制将会变得代价昂贵。

attention机制解决的根本问题是允许网络返回到输入序列，而不是把所有信息编码成固定长度的向量。也就是输出不仅仅取决于encoder的结果，还取决于输入序列。

正如我在上面提到，我认为使用attention有点儿用词不当。换句话说，attention机制只是简单地让网络模型访问它的内部存储器，也就是编码器的隐藏状态。在这种解释中，网络选择从记忆中检索东西，而不是选择“注意”什么。不同于典型的内存，这里的内存访问机制是弹性的，也就是说模型检索到的是所有内存位置的加权组合，而不是某个独立离散位置的值。弹性的内存访问机制好处在于我们可以很容易地用反向传播算法端到端地训练网络模型（虽然有non-fuzzy的方法，其中的梯度使用抽样方法计算，而不是反向传播）。

输入序列加权的过程，非常类似于查字典的过程，这也是后来的Transformer模型引入q,k,v（query,key,value）概念的原因。

论文：

《Learning to combine foveal glimpses with a third-order Boltzmann machine》

《Learning where to Attend with Deep Architectures for Image Tracking》

《Neural Machine Translation by Jointly Learning to Align and Translate》

Luong Attention and Bahdanau Attention

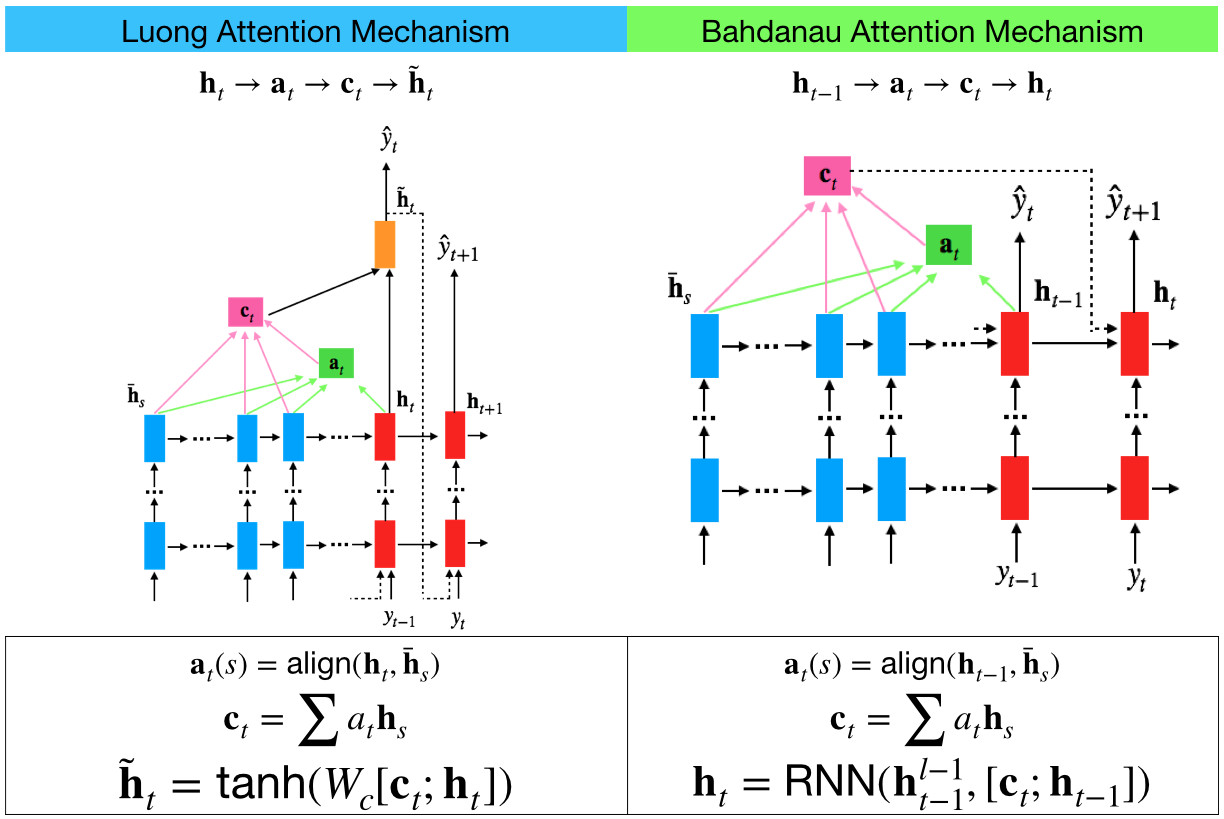
https://blog.csdn.net/sinat_34072381/article/details/106728056

Attention机制（Bahdanau attention & Luong Attention）

Neural Turing Machines

以下章节主要翻译自下文：

https://distill.pub/2016/augmented-rnns/

Attention and Augmented Recurrent Neural Networks

distill.pub虽然blog数量不多，但篇篇都是经典。背后站台的更有Yoshua Bengio、Ian Goodfellow、Andrej Karpathy等大牛。

该文主要讲述了Attention在RNN领域的应用。

---

NTM是一种使用Neural Network为基础来实现传统图灵机的理论计算模型。利用该模型，可以通过训练的方式让系统“学会”具有时序关联的任务流。

图灵机的详细定义可参见：

https://baike.baidu.com/item/图灵机

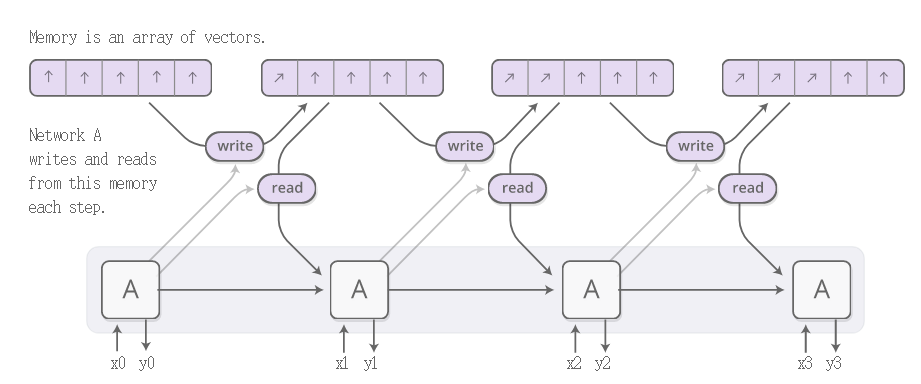
和传统图灵机相比，这里的memory中保存的是向量，我们的目标是根据输入序列，确定读写操作。具体的步骤如下图所示：

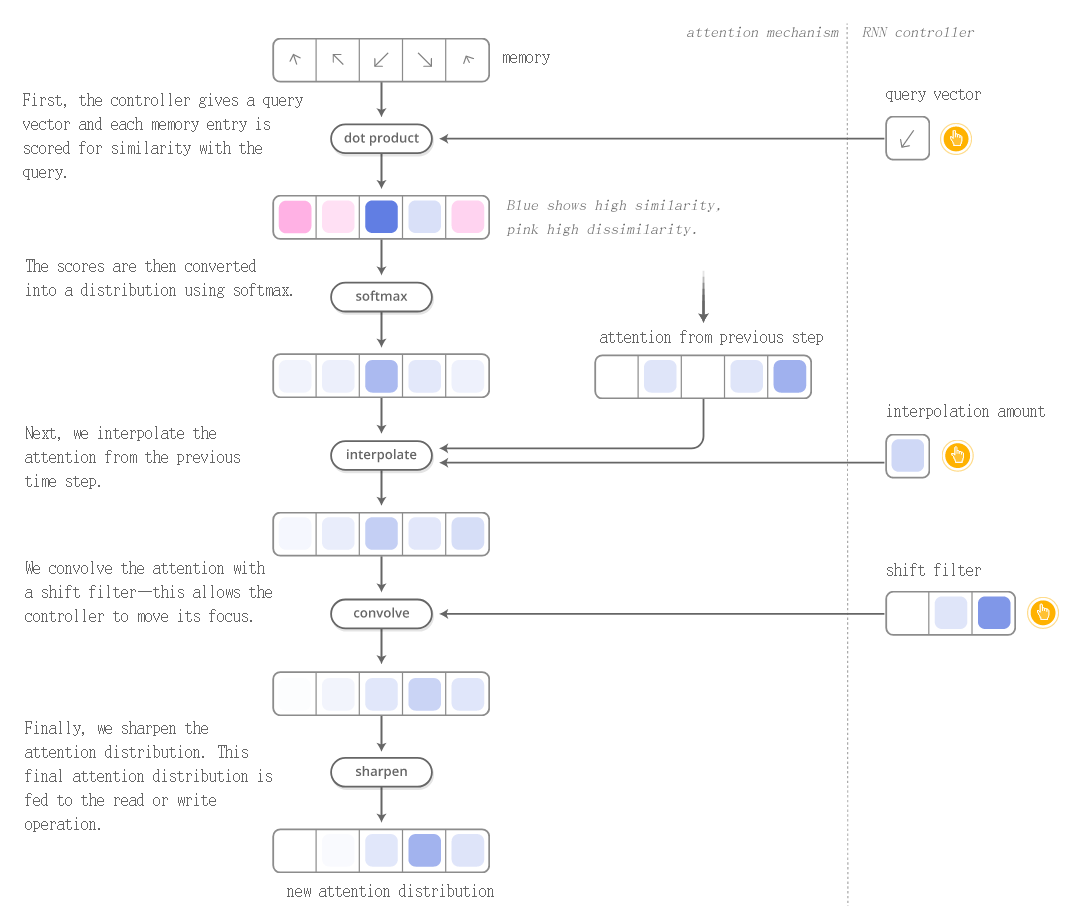
1.计算query vector和memory中每个vector的相似度。

2.将相似度softmax为一个分布。

3.用之前训练好的attention模型调整分布值。

4.图灵机的Shift操作也可以引入attention模型。

5.sharpen分布值，选择最终的读写操作。sharpen操作，实际上就是选择较大的概率值，而忽略较小的概率值。

Attentional Interfaces

以下是另外的一些Attention的用例。

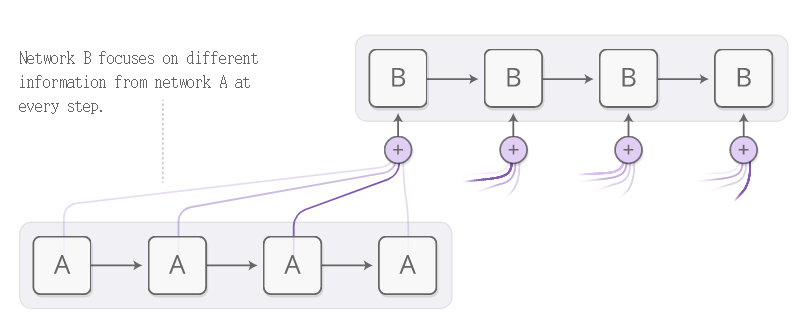
上图中，一个RNN模型可以输入另一个RNN模型的输出。它在每一步都会关注另一个RNN模型的不同位置。

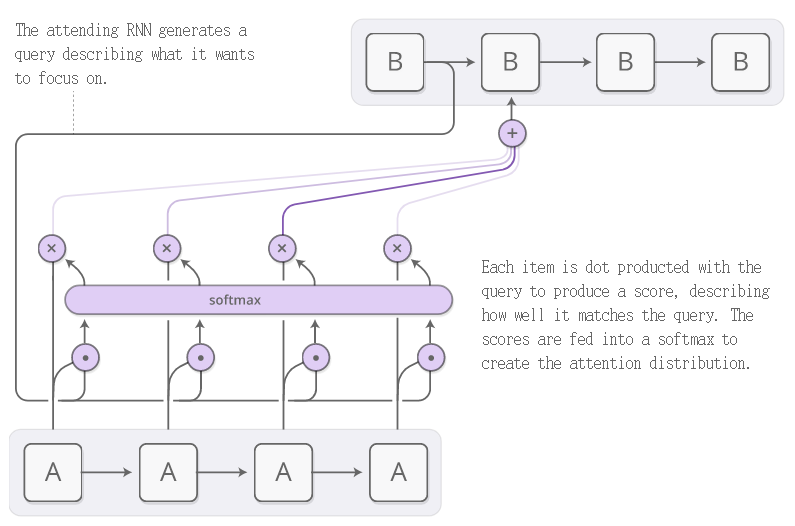
这是一个和NTM非常类似的模型。RNN模型生成一个搜索词描述其希望关注的位置。然后计算每条内容与搜索词的点乘得分，表示其与搜索词的匹配程度。这些分数经过softmax函数的运算产生聚焦的分布。

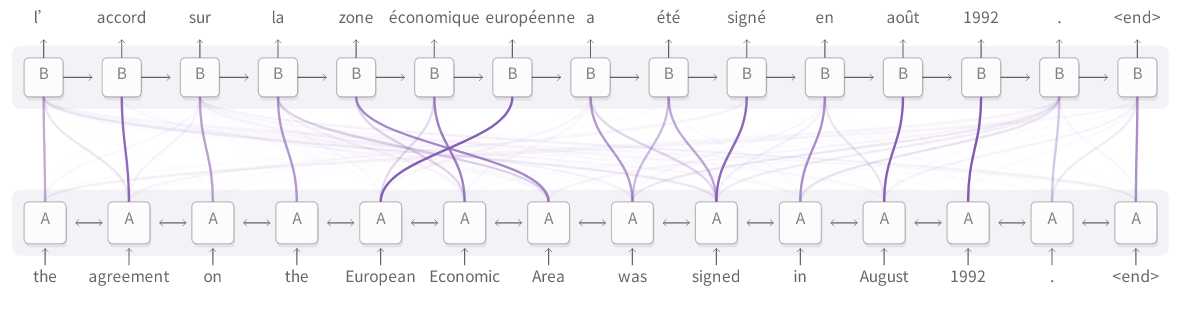
上图是语言翻译方面的模型。若用传统的序列到序列模型做翻译，需要把整个输入词汇串缩简为单个向量，然后再展开恢复为序列目标语言的词汇串。Attention机制则可以避免上述操作，RNN模型逐个处理输入词语的信息，随即生成相对应的词语。

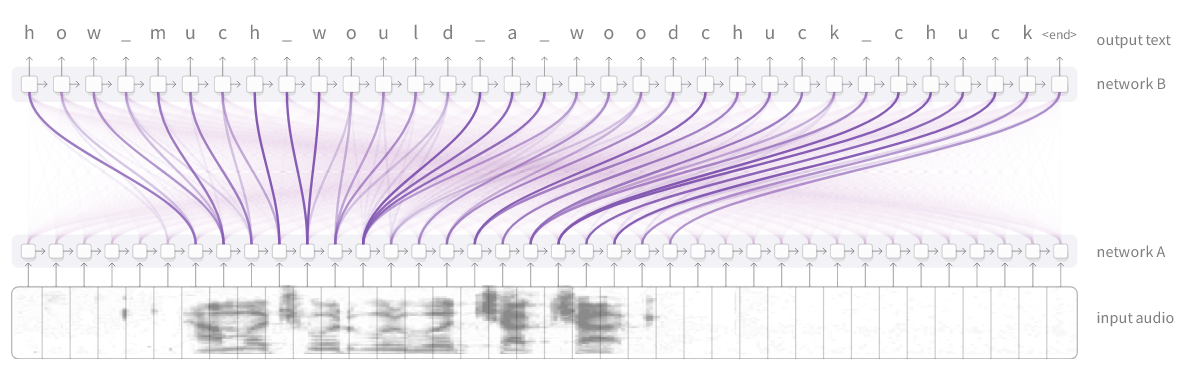
RNN模型之间的这类聚焦还有许多其它的应用。它可以用于语音识别，其中一个RNN模型处理语音信号，另一个RNN模型则滑动处理其输出，然后关注相关的区域生成文本内容。

Adaptive Computation Time

标准的RNN模型每一步所消耗的计算时间都相同。这似乎与我们的直觉不符。我们在思考难题的时候难道不需要更多的时间吗？

适应性计算时间（Adaptive Computation Time）是解决RNN每一步消耗不同计算量的方法。笼统地说：就是让RNN模型可以在每个时间片段内进行不同次数的计算步骤。

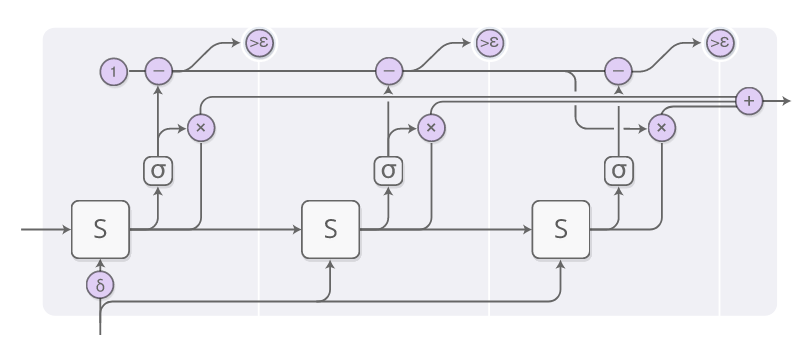
上图是ACT的网络结构图。下面来分步讲解一下。

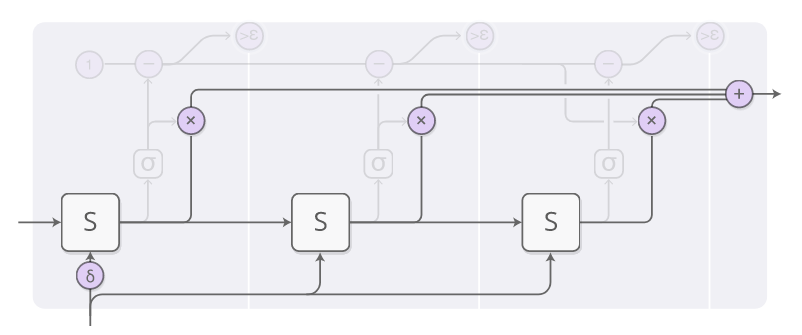
这一步就是典型的RNN+输出各个状态的带权重组合。

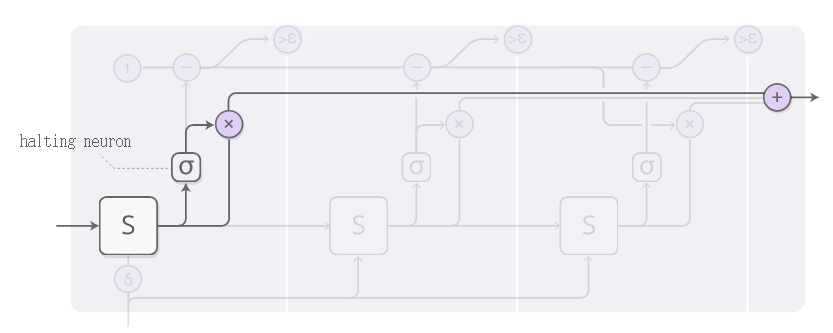
每一步的权重值由“halting neuron”决定。这个神经元事实上是一个sigmoid函数，输出一个终止权重，可以理解为需要在当前步骤终止的概率值。

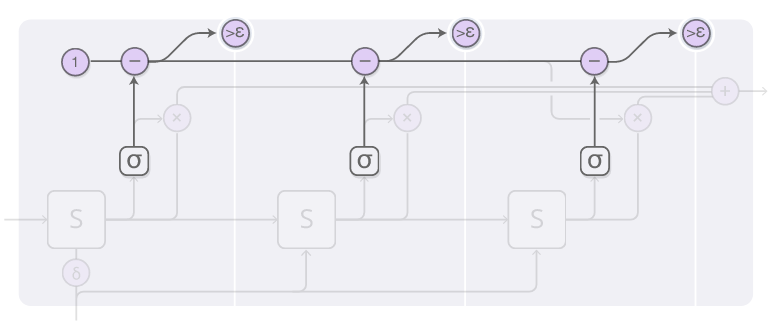
停止权重值的总和等于1，每一步结束后要减去相应的值。一旦这个值小于了epsilon，我们就停止计算。

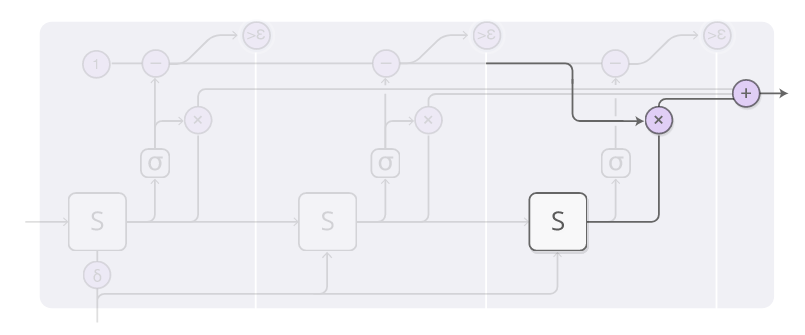
当训练Adaptive Computation Time模型时，可以在损失函数添加一项“ponder cost”，用来惩罚模型的累积计算时间。这一项的值越大，就更不倾向于降低计算时间。

花式Attention

Scaled Dot-Product Attention

以下内容摘自：

https://kexue.fm/archives/4765

《Attention is All You Need》浅读

《Attention is All You Need》是Google 2017年的作品。论文中提出了若干Attention的变种。比如下图所示的Scaled Dot-Product Attention。

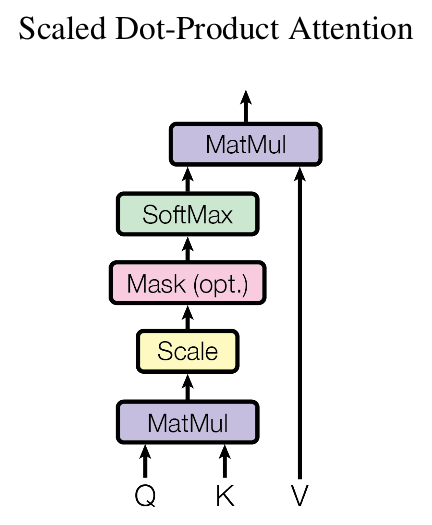
上图用公式表述就是：

\[Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d_k}}\right)\boldsymbol{V}\]

如果忽略激活函数softmax的话，那么事实上它就是三个\(n\times d_k,d_k\times m, m\times d_v\)的矩阵相乘，最后的结果就是一个\(n\times d_v\)的矩阵。于是我们可以认为：这是一个Attention层，将\(n\times d_k\)的序列Q编码成了一个新的\(n\times d_v\)的序列。

那怎么理解这种结构呢？我们不妨逐个向量来看。

\[Attention(\boldsymbol{q}_t,\boldsymbol{K},\boldsymbol{V}) = \sum_{s=1}^m \frac{1}{Z}\exp\left(\frac{\langle\boldsymbol{q}_t, \boldsymbol{k}_s\rangle}{\sqrt{d_k}}\right)\boldsymbol{v}_s\]

其中Z是归一化因子。事实上q,k,v分别是query,key,value的简写，K,V是一一对应的，它们就像是key-value的关系，那么上式的意思就是\(q_t\)这个query，通过与各个\(k_s\)内积的并softmax的方式，来得到\(q_t\)与各个\(v_s\)的相似度，然后加权求和，得到一个\(d_v\)维的向量。其中因子\(\sqrt{d_k}\)起到调节作用，使得内积不至于太大（太大的话softmax后就非0即1了，不够“soft”了），这也就是上图中的Scale。

概括的说就是：比较Q和K的相似度，以得到合适的V。

参考：

https://zhuanlan.zhihu.com/p/63895164

完全解析Tranformer转移力机制

https://mp.weixin.qq.com/s/I4FaPxj-8i3YHjaMoAniPQ

为什么有些深度学习网络要加入Product层？

https://www.zhihu.com/question/325839123

深度学习attention机制中的Q,K,V分别是从哪来的？