• Menelaus’ Theorem（续）
• 20世纪10大算法
• 自相关&互相关&卷积
• 马氏距离
• Hilbert Transform
• 无理数指数

Menelaus’ Theorem（续）

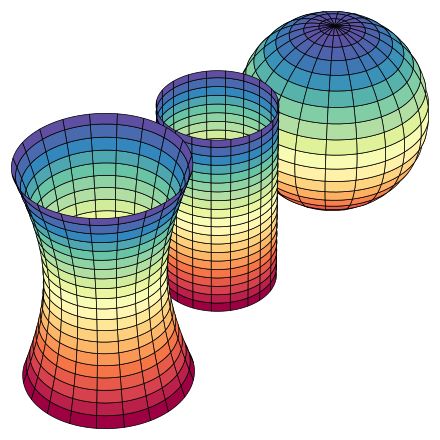
最左边的“束腰型”的曲线具有负的高斯曲率，中间的圆柱体曲面的高斯曲率为零，而最右边的球面具有正的高斯曲率。

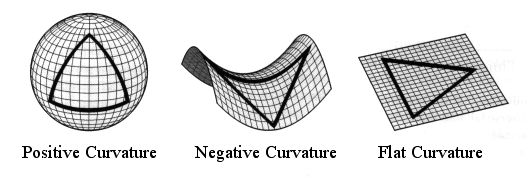
如果大家对高斯曲率还不能理解的话，还可用另外一个量来描述曲面的弯曲程度，那就是三角形的内角和，正曲率的曲面上三角形内角和大于180度，负曲率的曲面上三角形内角和小于180度，而平直平面上的三角形内角和等于180度。

https://www.zhihu.com/question/330796123

怎么理解万有引力的本质是空间的弯曲？

20世纪10大算法

2000年，IEEE评选出20世纪10大算法。名单如下：

1.Metropolis Algorithm for Monte Carlo

2.Simplex Method for Linear Programming

3.Krylov Subspace Iteration Methods

4.The Decompositional Approach to Matrix Computations

5.The Fortran Optimizing Compiler

6.QR Algorithm for Computing Eigenvalues

7.Quicksort Algorithm for Sorting

8.Fast Fourier Transform

9.Integer Relation Detection

10.Fast Multipole Method

详细内容参见：

http://www.uta.edu/faculty/rcli/TopTen/topten.pdf

中文版本：

http://blog.csdn.net/v_JULY_v/article/details/6127953

细数二十世纪最伟大的10大算法

类似的，还有奥地利符号计算研究所（Research Institute for Symbolic Computation，简称RISC）的Christoph Koutschan博士，针对计算机科学家所做的调查，选出的最重要的32个算法：

https://mp.weixin.qq.com/s/AFTaowkCz1pfFzaMDen-RA

计算机科学中最重要的32个算法

https://mp.weixin.qq.com/s/CCN4w3_n8NVrmz4xE-GWlQ

八大应用公式

自相关&互相关&卷积

1.自相关（Autocorrelation）。这个最简单，就是平移之后，自己和自己比。显然当平移为0的时候，自相关值最大，因此这类操作通常用于信号的检测。信号接收端模拟发射端的信号序列，对实际接收到的信号进行相关操作，只有当两者的序列接近重合时，才会检测到信号峰值。

2.互相关（Cross-correlation）。检测两个序列的相似度，显然两者越相似，互相关值越大。这在统计学方面用的比较多。

在信号处理领域，Cross-correlation常用于信号的调制和解调。下图就是常见的正交调制解调（orthogonal modulation and demodulation）的原理图：

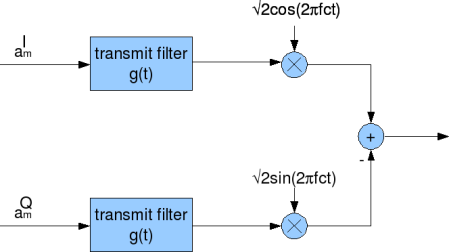
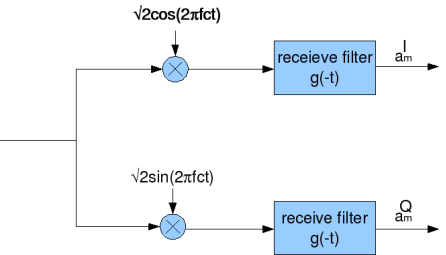
3.卷积（Convolution）。卷积主要用于线性时不变系统的信号处理。相比于互相关操作，卷积有个旋转180度的操作，这里解释一下它的物理意义。

例如，当一个拳击选手遭到对方连续两次击打身体的同一部位时，第二次被击打时他感觉到的疼痛是第一次被击打所遗留的疼痛与第二次被击打的疼痛之和。即：

\[f(2)=f_1(2)+f_2(1)\]

其中，\(f_i(t)\)中，i表示第i次击打，t表示击打发生之后经过的时间。可以看出i和t的顺序正好是相反的，这也就是Convolution这个名词的本意。这里假设g为常数。

正式定义：

\[[f \ast g] (t)\equiv \int_ {-\infty}^ {\infty} f (\tau) g (t-\tau) d \tau\]

注意：这里实际上有一个\(\tau+t-\tau=t\)约束。

4.这三个操作在离散域最终都可以变为求和操作，也就是向量内积运算。我们一般使用\(a\cdot b\)或者\(\langle a,b\rangle\)表示向量的内积运算。即：

\[\langle a,b\rangle=a_0b_0+a_1b_1+\dots+a_nb_n\]

卷积最经典的应用，当属信号处理领域的傅立叶变换：

\[\mathcal{F}\{f * g\} = k\cdot \mathcal{F}\{f\}\cdot \mathcal{F}\{g\}\]

不管怎么组合，自相关&互相关&卷积实际上都是向量的内积运算。

除此之外，还有利用向量张量积运算的相关矩阵。同样的，也有自相关矩阵和互相关矩阵。

4.循环卷积（Circular convolution）。

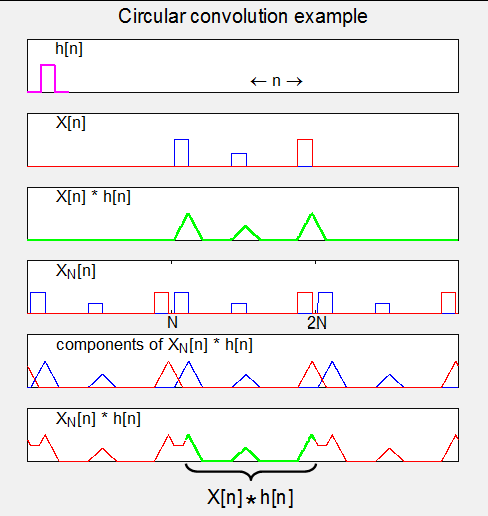
参考：

https://mp.weixin.qq.com/s/R0LTEEYY1jCbSS-f6KlIzw

有限长序列的线性卷积和圆周卷积

https://mp.weixin.qq.com/s/UrWEZ5fMGxj5Ngbi6Y1nFg

如何通俗易懂地解释卷积？

https://mp.weixin.qq.com/s/gZ-LIBMUcqmSz0D1jPyPlA

很详细的讲解什么以及为什么是卷积（Convolution）

马氏距离

Mahalanobis Distance是印度现代统计学之父Prasanta Chandra Mahalanobis于1936年提出的概念。

Prasanta Chandra Mahalanobis，1893~1972，印度统计学家，剑桥大学博士，印度统计研究所创始人。
印度的重点研究所一般叫做Institute of National Importance，共92所。Indian Statistical Institute是其中唯一一所和统计相关的研究所。教师255，学生375，这得是多精英的教育啊。其计算机科学专业排名印度第2。

p维空间的两点（两个p维向量x,y）的欧氏距离定义为：

\[d_E(x,y)=\sqrt{(x_1-y_1)^2+\dots+(x_p-y_p)^2}=\sqrt{(x-y)^T(x-y)}（公式1）\]

因此，x到原点的距离为：

\[\parallel x\parallel=d_E(x,0)=\sqrt{(x_1)^2+\dots+(x_p)^2}（公式2）\]

也就是：

\[x_1^2+\dots+x_p^2=\parallel x\parallel^2（公式3）\]

这实际上是个正球体的方程，也就是说观测数据x的各个分量对x至中心的欧氏距离贡献是相等的。然而在统计学中我们希望寻求这样一种距离，它的各个分量的作用程度是不同的。差别较大的分量应该接受较小的权重。

于是，公式3可变形为椭球体方程：

\[(\frac{x_1}{s_1})^2+\dots+(\frac{x_p}{s_p})^2=\parallel x\parallel^2（公式4）\]

其中的\(s_i\)表示i分量的权重。

公式4进一步整理，并扩展到两个p维向量x,y，可得马氏距离定义：

\[d_M(x,y)=\sqrt{(\frac{x_1-y_1}{s_1})^2+\dots+(\frac{x_p-y_p}{s_p})^2}=\sqrt{(x-y)^TD^{-1}(x-y)}（公式5）\]

其中，\(D=diag(s_1^2,\dots,s_p^2)\)。

注意：这里p维向量是正交基，否则的话，D将不是主对角线矩阵，而是一个普通的协方差矩阵。显然如果D为单位矩阵的话，马氏距离就变成了欧氏距离。

马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关。比如体重和身高数据，如果采用欧氏距离，则会由于量纲的不同，而无法比较。

由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。它的缺点是夸大了变化微小的变量的作用。

马氏距离的特点还包括：

1）马氏距离的计算是建立在总体样本的基础上的，这一点可以从上述协方差矩阵的解释中可以得出，也就是说，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；

2）在计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离来代替马氏距离，也可以理解为，如果样本数小于样本的维数，这种情况下求其中两个样本的距离，采用欧式距离计算即可。

3）还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如A（3，4），B（5，6）；C（7，8），这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧式距离计算。

4）在实际应用中“总体样本数大于样本的维数”这个条件是很容易满足的，而所有样本点出现3）中所描述的情况是很少出现的，所以在绝大多数情况下，马氏距离是可以顺利计算的，但是马氏距离的计算是不稳定的，不稳定的来源是协方差矩阵，这也是马氏距离与欧式距离的最大差异之处。

---

Feature scaling，常见的提法有“特征归一化”、“标准化”，是数据预处理中的重要技术。

与距离计算无关的概率模型，不需要feature scaling，比如Naive Bayes；

与距离计算无关的基于树的模型，不需要feature scaling，比如决策树、随机森林等，树中节点的选择只关注当前特征在哪里切分对分类更好，即只在意特征内部的相对大小，而与特征间的相对大小无关。

---

参考：

https://mp.weixin.qq.com/s/xiVmQjJDqY_iOBz_bB_O7g

距离度量，浅谈！

https://mp.weixin.qq.com/s/dpeuDMLIyXyhGYrwaLt-PA

机器学习特性缩放的介绍，什么时候为什么使用

https://mp.weixin.qq.com/s/TF6d9NRz0lDFQeC_K3CVaw

为什么要做特征归一化/标准化？

Hilbert Transform

\[g(y)=H[f(x)]=\frac{1}{\pi}\int_{-\infty}^{+\infty}\frac{f(x)\mathrm{d}x}{x-y}\] \[f(x)=H^{-1}[g(y)]=-\frac{1}{\pi}\int_{-\infty}^{+\infty}\frac{g(y)\mathrm{d}y}{y-x}\]

这里的积分是Cauchy Principal Value积分。

https://www.sohu.com/a/223899744_100011708

希尔伯特变换（Hilbert Transform）简介及其物理意义

https://www.cnblogs.com/hdu-zsk/p/4799470.html

Hilbert-Huang Transform（希尔伯特-黄变换）

https://mp.weixin.qq.com/s/avLWHXj2JkjXOomCipj8kA

使用希尔伯特-黄变换（HHT）进行时间序列分析

无理数指数

整数指数：

\[2^3=2\times 2\times 2\]

有理数指数（利用指数乘法特性进行扩展）：

\[2^{\frac12}\times 2^{\frac12}=2^{\frac12+\frac12}=2\]

因此：

\[2^{\frac12}=\sqrt{2}\]

无理数指数（利用极限进行扩展）：

\[2^3, 2^{3.1}, 2^{3.14},2^{3.141},2^{3.1415},2^{3.14159},\dots\]

趋向于一个确定的值。

因此：

\[\lim_{n \rightarrow \infty}{2^{\frac{\lfloor10^n\pi\rfloor}{10^n}}}=2^{\pi}\]

https://www.zhihu.com/question/434836259

2的π次方是啥东西？