math » 线性代数(三)——向量的范数
2022-01-09 :: 5763 Words特征值和奇异值
矩阵的奇异值(续)
类似的,我们定义共轭矩阵\(M^*_{ij}=\overline{M_{ji}}\),这实际上就是矩阵M转置之后,再将每个元素值设为它的共轭复数。因此:
\[M^*=(\overline M)^T=\overline{M^T}\]仿照着复数的写法,矩阵M可以表示为:\(M=S\sqrt{M^*M}\)
这里的S表示等距同构。(单位向量相当于给模一个旋转变换,也就是等距同构。)由于\(\sqrt{M^*M}\)是正定对称方阵,因此它实际上也是能够被正交化的。所以对于一般矩阵来说,我们总能够找到两个正交基,并在这两个基之间进行投影变换。
注意:我们刚才是用与复数类比的方式,得到投影变换矩阵\(\sqrt{M^*M}\)。但是类比不能代替严格的数学证明。幸运的是,上述结论已经被严格证明了。
我们将矩阵\(\sqrt{M^*M}\)的特征值,称作奇异值(Singular value)。可以看出,如果M是对称方阵的话,则M的奇异值等于M的特征值的绝对值。
参见:
https://www.zhihu.com/answer/53804902
奇异值的物理意义是什么?
http://www.ams.org/samplings/feature-column/fcarc-svd
We Recommend a Singular Value Decomposition
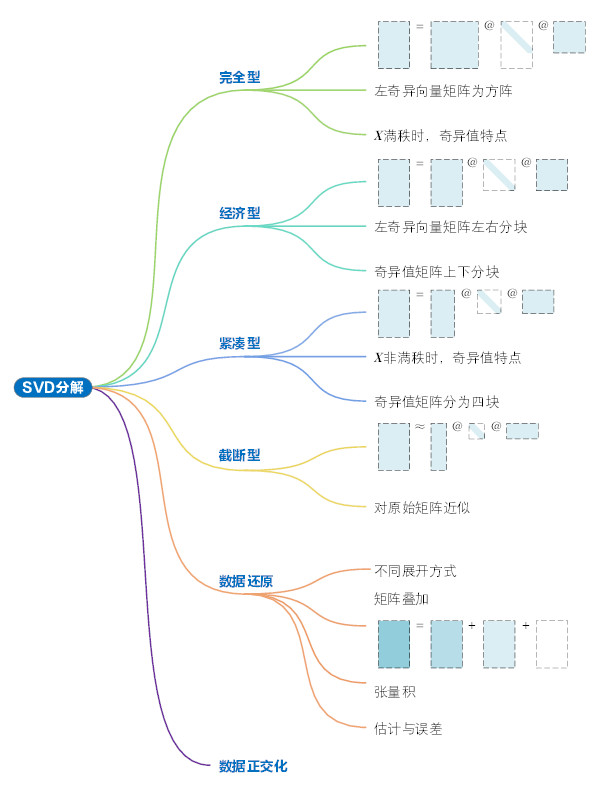
奇异值分解
奇异值分解(Singular value decomposition,SVD)定理:
设\(M\in R^{m\times n}\),则必存在正交矩阵\(U=[u_1,\dots,u_m]\in R^{m\times m}\)和\(V=[v_1,\dots,v_n]\in R^{n\times n}\)使得:
\[U^TMV=\begin{bmatrix} \Sigma_r & 0 \\ 0 & 0 \end{bmatrix}\]其中,\(\Sigma_r=diag(\sigma_1,\dots,\sigma_r),\sigma_1\ge \dots\ge \sigma_r>0\)。
当M为复矩阵时,将U、V改为酉矩阵(unitary matrix)即可。(吐槽一下,酉矩阵这个翻译真的好烂,和天干地支半毛钱关系都没有。)
奇异值分解也可写为另一种形式:
\[M=U\Sigma V^*\]其几何意义如下图所示:
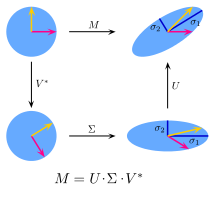
它意味着任何对(列)向量x的线性变换,都可以分解为旋转、拉伸、旋转三个步骤。
虽然,我们可以通过计算矩阵\(\sqrt{M^*M}\)的特征值的方法,计算奇异值,然而这个方法的计算量十分巨大。1965年,Gene Howard Golub和William Morton Kahan发明了目前较为通用的算法。但该方法比较复杂,这里不作介绍。
Gene Howard Golub,1932~2007,美国数学家,斯坦福大学教授。
William Morton Kahan,1933年生,加拿大数学家,多伦多大学博士,UCB教授。图灵奖获得者(1989)。IEEE-754标准(即浮点数标准)的主要制订者,被称为“浮点数之父”。ACM院士。
参见:
http://www.doc88.com/p-089411326888.html
SVD(奇异值分解)算法及其评估
https://mp.weixin.qq.com/s/46oOYoL486WZ4oPwgLrrrQ
奇异值分解SVD原理与应用详解
https://mp.weixin.qq.com/s/1pg8jY1R-8kJKu1L_RPLkg
奇异值分解(SVD)原理
https://mp.weixin.qq.com/s/tZqkbJ18ANCcA7ndWmJEGw
奇异值分解简介:从原理到基础机器学习应用
https://mp.weixin.qq.com/s/Z0ZkQlZDKUSJEWVq7Vi6Cg
奇异值分解(SVD)原理与在降维中的应用
https://mp.weixin.qq.com/s/bYTS9UXH7ecwrq6_WIangw
如何让奇异值分解(SVD)变得不“奇异”?
https://mp.weixin.qq.com/s/54_qLczv8ooqoQQioIeUww
通俗易懂的讲解奇异值分解(SVD)和主成分分析(PCA)
https://mp.weixin.qq.com/s/R54brOW-TBD3UGJUwE2QOg
SVD加速:rSVD
向量的范数
范数(norm,也叫模)的定义比较抽象,这里我们使用闵可夫斯基距离,进行一个示意性的介绍。
Minkowski distance的定义:
\[d(x,y)=\sqrt[\lambda]{\sum_{i=1}^{n}\mid x_i-y_i\mid^{\lambda}}\]Hermann Minkowski(1864-1909),德国数学家,哥廷根大学数学教授,爱因斯坦的老师。
这里的\(\lambda\)就是范数。
范数可用符号\(\|x\|_\lambda\)表示。常用的有:
\[\|x\|_1=\mid x_1\mid +\dots+\mid x_n\mid\] \[\|x\|_2=\sqrt{x_1^2+\dots+x_n^2}\] \[\|x\|_\infty=max(\mid x_1\mid ,\dots,\mid x_n\mid )\]显然,当\(\lambda=2\)时,该距离为Euclid Distance。
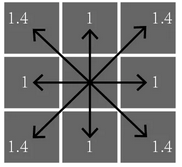
当\(\lambda=1\)时,也被称为CityBlock Distance或Manhattan Distance(曼哈顿距离,以纽约曼哈顿地区的街道形状得名)。
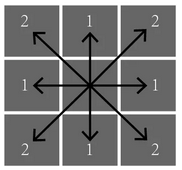
当\(\lambda=\infty\)时,叫做Chebyshev distance。
Pafnuty Lvovich Chebyshev,1821~1894,俄罗斯数学家,莫斯科大学博士,圣彼得堡大学教授。俄罗斯数学的奠基人,他创建的圣彼得堡学派,是20世纪俄罗斯最主要的数学流派。
这里不做解释的给出如下示意图:
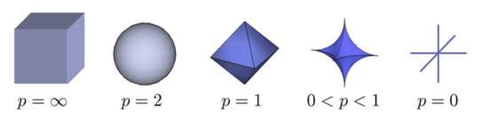
其中,L0范数表示向量中非0元素的个数。上图中的图形被称为\(l_p\) ball。表征在同一范数条件下,具有相同距离的点的集合。
范数满足如下不等式:
\[\|A+B\|\le \|A\|+\|B\|(三角不等式)\]向量范数推广可得到矩阵范数。某些矩阵范数满足如下公式:
\[\|A\cdot B\|\le \|A\|\cdot\|B\|\]这种范数被称为相容范数。
矩阵范数要比向量范数复杂的多,还包含一些不可以由向量范数来诱导的范数,如Frobenius范数。而且只有极少数矩阵范数,可由简单表达式来表达。这里篇幅有限,不再赘述。
Ferdinand Georg Frobenius,1849~1917,德国数学家,哥廷根大学博士(1870),University of Berlin和ETH Zurich教授。他在椭圆函数、微分方程、数论和群论等领域有杰出贡献。矩阵的秩就是他提出来的。
病态矩阵
现在有线性系统\(Ax = b\):
\[\begin{bmatrix} 400 & -201 \\-800 & 401 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=\begin{bmatrix} 200 \\ -200 \end{bmatrix}\]很容易得到解为:\(x_1=-100,x_2=-200\)。如果在样本采集时存在一个微小的误差,比如,将 A矩阵的系数400改变成401:
\[\begin{bmatrix} 401 & -201 \\-800 & 401 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=\begin{bmatrix} 200 \\ -200 \end{bmatrix}\]则得到一个截然不同的解:\(x_1=40000,x_2=79800\)。
当解集x对A和b的系数高度敏感,那么这样的方程组就是病态的 (ill-conditioned/ill-posed)。
从上例的情况来看,矩阵的行向量\(\begin{bmatrix} 400 & -201\end{bmatrix}\)和\(\begin{bmatrix} -800 & 401\end{bmatrix}\)实际上是过于线性相关了,从而导致矩阵已经接近奇异矩阵(near singular matrix)。
病态矩阵实际上就是奇异矩阵和近奇异矩阵的另一个说法。
参见:
http://www.cnblogs.com/daniel-D/p/3219802.html
病态矩阵与条件数
矩阵的条件数
我们首先假设向量b受到扰动,导致解集x产生偏差,即:
\[A(x+\Delta x)=b+\Delta b\]也就是:
\[A\Delta x=\Delta b\]因此,由矩阵相容性可得:
\[\|\Delta x\|\le \|A^{-1}\|\cdot\|\Delta b\|\]同时,由于:
\[\|A\|\cdot\|x\|\ge\|b\|\]所以:
\[\frac{\|\Delta x\|}{\|A\|\cdot\|x\|}\le \frac{\|A^{-1}\|\cdot\|\Delta b\|}{\|b\|}\]即:
\[\frac{\|\Delta x\|}{\|x\|}\le \frac{\|A\|\cdot\|A^{-1}\|\cdot\|\Delta b\|}{\|b\|}\]我们定义矩阵的条件数\(K(A)=\|A\|\cdot\|A^{-1}\|\),则上式可写为:
\[\frac{\|\Delta x\|}{\|x\|}\le K(A)\frac{\|\Delta b\|}{\|b\|}\]同样的,我们针对A的扰动,所导致的x的偏差,也可得到类似的结论:
\[\frac{\|\Delta x\|}{\|x+\Delta x\|}\le K(A)\frac{\|\Delta A\|}{\|A\|}\]可见,矩阵的条件数是描述输入扰动对输出结果影响的量度。显然,条件数越大,矩阵越病态。
然而这个定义,在病态矩阵的条件下,并不能直接用于数值计算。因为浮点数所引入的微小的量化误差,也会导致求逆结果的很大误差。所以通常情况下,一般使用矩阵的特征值或奇异值来计算条件数。
假设A是2阶方阵,它有两个单位特征向量\(x_1,x_2\)和相应的特征值\(\lambda_1,\lambda_2\)。
由之前的讨论可知,\(x_1,x_2\)是相互正交的。因此,向量b能够被\(x_1,x_2\)的线性组合所表示,即:
\[b=mx_1+nx_2=\frac{m}{\lambda_1}\lambda_1x_1+\frac{n}{\lambda_2}\lambda_2x_2=A(\frac{m}{\lambda_1}x_1+\frac{n}{\lambda_2}x_2)\]从这里可以看出,b在\(x_1,x_2\)上的扰动,所带来的影响,和特征值\(\lambda_1,\lambda_2\)有很密切的关系。奇异值实际上也有类似的特点。
因此,一般情况下,条件数也可以由最大奇异值与最小奇异值之间的比值,或者最大特征值和最小特征值之间的比值来表示。这里的最大和最小,都是针对绝对值而言的。
参见:
https://en.wikipedia.org/wiki/Condition_number
矩阵规则化
病态矩阵处理方法有很多,这里只介绍矩阵规则化(regularization)方法。
机器学习领域,经常用到各种损失函数(loss function)。这里我们用:
\[\min_f \sum_{i=1}^nV(f(\hat x_i),\hat y_i)\]表示损失函数。
当样本数远小于特征向量维数时,损失函数所表示的矩阵是一个稀疏矩阵,而且往往还是一个病态矩阵。这时,就需要引入规则化因子用以改善损失函数的稳定性:
\[\min_f \sum_{i=1}^nV(f(\hat x_i),\hat y_i)+\lambda R(f)\]其中的\(\lambda\)表示规则化因子的权重。
稀疏矩阵并不一定是病态矩阵,比如单位阵就不是病态的。但是从系统论的角度,高维空间中样本量的稀疏,的确会带来很大的不确定性。可类比下围棋,棋子过于稀疏的地方,只能称作势力范围,而不能称作实地。
函数V(又叫做Fit measure)和R(又叫做Entropy measure),在不同的算法中,有不同的取值。
比如,在Ridge regression问题中:
\[\text{Fit measure}:\|Y-X\beta\|_2,\text{Entropy measure}:\|\beta\|_2\]Ridge regression问题中规则化方法,又被称为\(L_2\) regularization,或Tikhonov regularization。
Andrey Nikolayevich Tikhonov,1906~1993,苏联数学家和地球物理学家。大地电磁学的发明人之一。苏联科学院院士。著有《Solutions of Ill-posed problems》一书。
更多的V和R取值参见:
https://en.wikipedia.org/wiki/Regularization_(mathematics)
从形式上来看,对比之前提到的拉格朗日函数,我们可以发现规则化因子,实际上就是给损失函数增加了一个约束条件。它的好处是增加了解向量的稳定度,缺点是增加了数值解和真实解之间的误差。

您的打赏,是对我的鼓励
