math » 线性代数（一）——概述, 矩阵&向量的积, 三角矩阵的求逆问题
2022-01-07 :: 7144 Words概述
虽然Andrew Ng的讲义中已经包含了一个线性代数方面的简介文章，然而真的就只是简介而已，好多内容都没有。
这里推荐一本书《Matrix Methods in Data Mining and Pattern Recognition》。
作者：Lars Eld´en，执教于Linköping University数学系。
http://www.cnblogs.com/daniel-D/p/3204508.html
这是daniel-D写的中文笔记。
这一部分的内容属于数值计算领域，涉及的概念虽然不复杂，但提出一个高效算法，仍然不是件容易的事情。
还有另外一本书《Liner Algebra Done Right》，也值得推荐。这本书从定义矩阵算子，而不是通过行列式，来解释各种线性代数原理，提供了一种独特的视角。因为算子是有明确的几何或物理意义的，而行列式则不然。
作者：Sheldon Jay Axler，1949年生，美国数学家。普林斯顿大学本科，UCB博士，MIT博士后，San Francisco State University教授。美国的数学系基本就是本科和博士，很少有硕士。因为数学，尤其是理论数学，需要高度的抽象思维能力，半调子的硕士，既不好找工作，也不好搞科研。
《Linear Algebra Done Wrong》，这是布朗大学的Sergei Treil教授的著作，不知道书名是否有恶搞前书的意味…
该书电子版：
https://www.math.brown.edu/~treil/papers/LADW/LADW.html
https://mp.weixin.qq.com/s/4NRkrkV_M2b_IpnpCTn05w
一图胜千言，这本交互式线代教科书让你分分钟理解复杂概念，佐治亚理工出品
https://mp.weixin.qq.com/s/xWiRzBmK1JiGldMiq3BkTg
伯克利一份简明《机器学习数学基础》丝滑入门手册，47页pdf
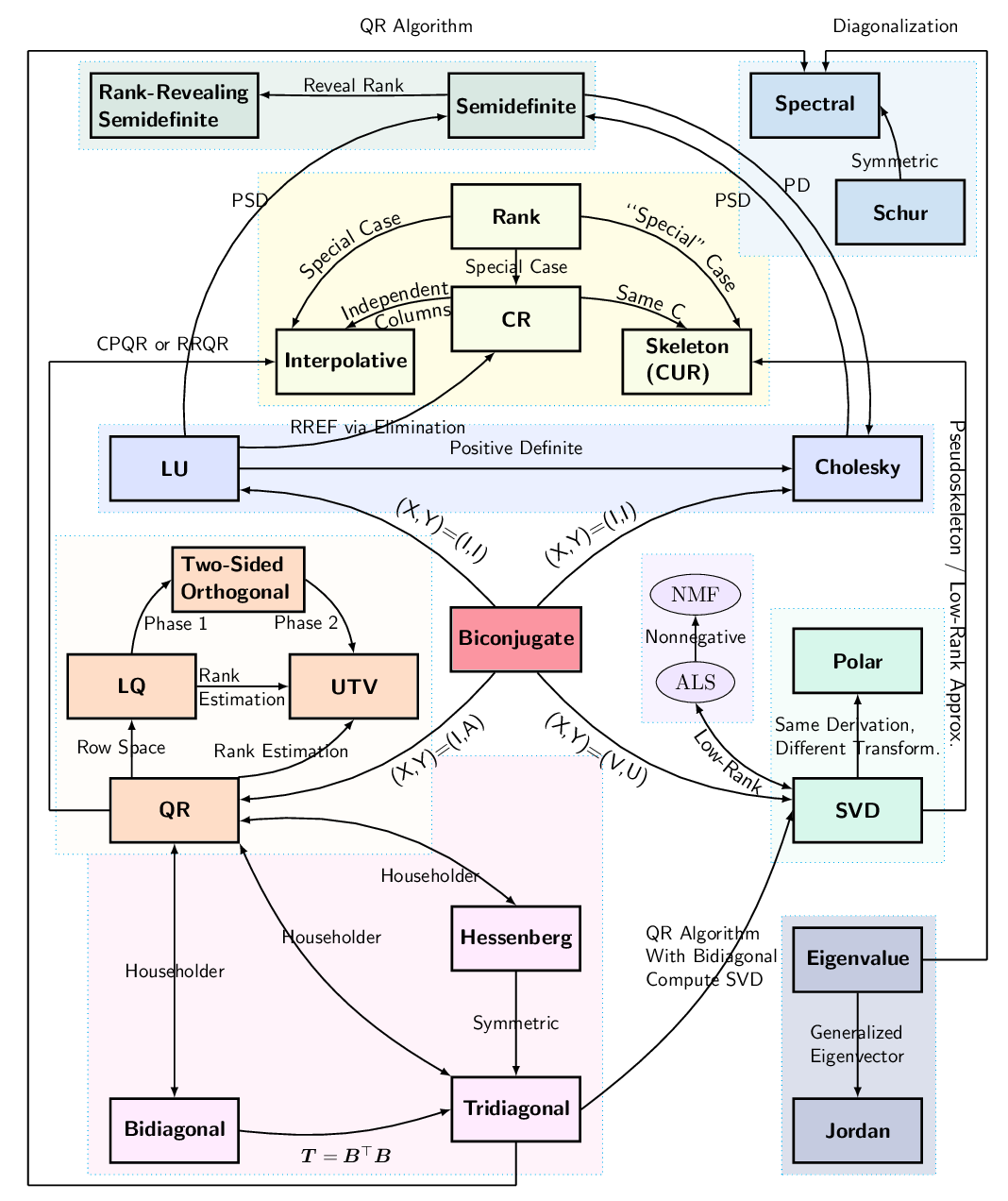
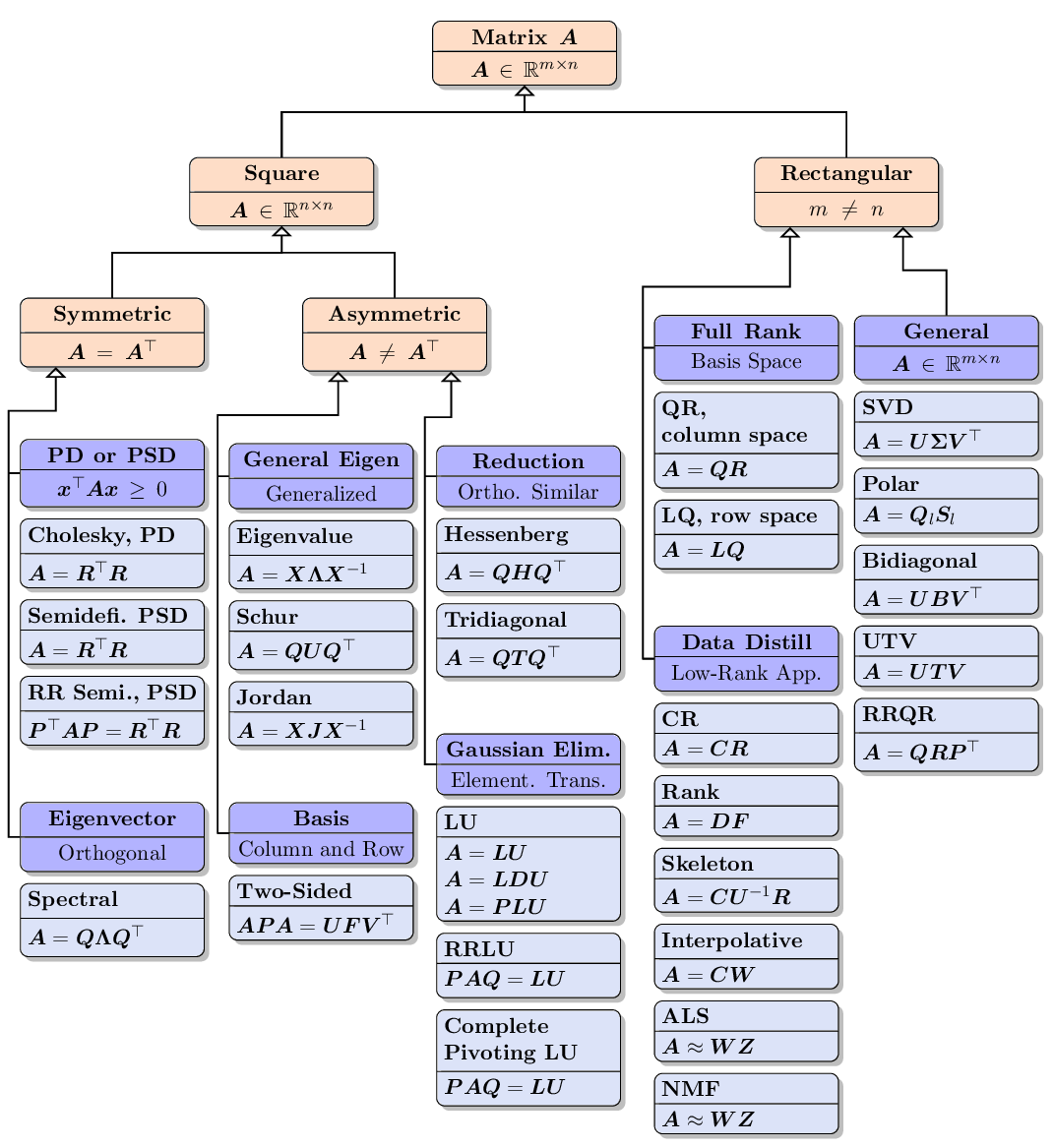
《Matrix Decomposition and Applications》
矩阵&向量的积
矩阵&向量有很多种积的定义，特罗列如下：
向量的数乘
Scalar multiplication的定义如下：
\[c\mathbf{a}=c[a_1,\dots,a_n]=[ca_1,\dots,ca_n]\]向量的点积
Dot product，又称inner product。
代数定义：
\[\mathbf{a}\cdot\mathbf{b}=\sum_{i=1}^n a_ib_i=a_1b_1+a_2b_2+\cdots+a_nb_n\]几何定义：
\[\mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\ \|\mathbf{b}\|\cos(\theta)\]复变积分定义：
\[\left\langle \psi , \chi \right\rangle = \int_a^b \psi(x) \overline{\chi(x)} d x\]矩阵的积
matrix product的定义如下（以3阶方阵为例）：
\[\mathbf{AB} = \begin{bmatrix} a & b & c \\ p & q & r \\ u & v & w \end{bmatrix} \begin{bmatrix} \alpha & \beta & \gamma \\ \lambda & \mu & \nu \\ \rho & \sigma & \tau \\ \end{bmatrix} =\begin{bmatrix} a\alpha + b\lambda + c\rho & a\beta + b\mu + c\sigma & a\gamma + b\nu + c\tau \\ p\alpha + q\lambda + r\rho & p\beta + q\mu + r\sigma & p\gamma + q\nu + r\tau \\ u\alpha + v\lambda + w\rho & u\beta + v\mu + w\sigma & u\gamma + v\nu + w\tau \end{bmatrix}\]可以看出，积矩阵的每个元素是矩阵A、B相应行列向量的内积。
向量的向量积
Cross product是一个向量，其定义如下：
\[\mathbf{a} \times \mathbf{b} = \left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \sin (\theta) \ \mathbf{n}\]它还有个更出名的定义：
\[\mathbf{u\times v} = \begin{vmatrix} \mathbf{i}&\mathbf{j}&\mathbf{k}\\ u_1&u_2&u_3\\ v_1&v_2&v_3\\ \end{vmatrix}\]由于Cross product和a、b所在平面垂直，因此多用于求解平面的法向量，且该法向量的方向符合“右手定则”。
向量的混合积
triple product，又称mixed product或box product。
\[\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c}) \equiv \det \begin{bmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \\ \end{bmatrix}={\rm det}\left(\mathbf{a},\mathbf{b},\mathbf{c}\right)\]混合积相当于求解以a、b、c为棱的六面体的体积。由体积的唯一性，易得混合积具有交换律和结合律。
向量的笛卡尔积
Cartesian product实际上是集合论中的概念。
\[A\times B = \{1,2\} \times \{3,4\} = \{(1,3), (1,4), (2,3), (2,4)\}\]向量的张量积
Tensor product，又称outer product。
\[\begin{align}\mathbf{u} \otimes \mathbf{v} = \mathbf{u} \mathbf{v}^\mathrm{T} = \begin{bmatrix}u_1 \\ u_2 \\ u_3 \\ u_4\end{bmatrix} \begin{bmatrix}v_1 & v_2 & v_3\end{bmatrix} = \begin{bmatrix}u_1v_1 & u_1v_2 & u_1v_3 \\ u_2v_1 & u_2v_2 & u_2v_3 \\ u_3v_1 & u_3v_2 & u_3v_3 \\ u_4v_1 & u_4v_2 & u_4v_3\end{bmatrix}\end{align}\]可以看出，Tensor product和Cartesian product，虽然形式上都是各向量的组合，然而前者是2维的，而后者是1维的。
外积这个术语，在中文中也可以指Cross product，所以最好避免使用外积这个术语，避免混淆。
矩阵的张量积
张量积推广到矩阵，即所谓Kronecker product。
\[\mathbf{A}\otimes\mathbf{B} = \begin{bmatrix} a_{11} \mathbf{B} & \cdots & a_{1n}\mathbf{B} \\ \vdots & \ddots & \vdots \\ a_{m1} \mathbf{B} & \cdots & a_{mn} \mathbf{B} \end{bmatrix}\]Leopold Kronecker，1823～1891，德国数学家。柏林大学博士和教授。导师Dirichlet。他最牛逼的地方是，当Riemann去世的时候，拒绝了哥廷根大学的offer。而这个位置的前任分别是：Carl Gauss、Dirichlet、Riemann。
Hadamard product
又叫Schur product或entrywise product。
\[\left(\begin{array}{ccc} \mathrm{a}_{11} & \mathrm{a}_{12} & \mathrm{a}_{13}\\ \mathrm{a}_{21} & \mathrm{a}_{22} & \mathrm{a}_{23}\\ \mathrm{a}_{31} & \mathrm{a}_{32} & \mathrm{a}_{33} \end{array}\right) \circ \left(\begin{array}{ccc} \mathrm{b}_{11} & \mathrm{b}_{12} & \mathrm{b}_{13}\\ \mathrm{b}_{21} & \mathrm{b}_{22} & \mathrm{b}_{23}\\ \mathrm{b}_{31} & \mathrm{b}_{32} & \mathrm{b}_{33} \end{array}\right) = \left(\begin{array}{ccc} \mathrm{a}_{11}\, \mathrm{b}_{11} & \mathrm{a}_{12}\, \mathrm{b}_{12} & \mathrm{a}_{13}\, \mathrm{b}_{13}\\ \mathrm{a}_{21}\, \mathrm{b}_{21} & \mathrm{a}_{22}\, \mathrm{b}_{22} & \mathrm{a}_{23}\, \mathrm{b}_{23}\\ \mathrm{a}_{31}\, \mathrm{b}_{31} & \mathrm{a}_{32}\, \mathrm{b}_{32} & \mathrm{a}_{33}\, \mathrm{b}_{33} \end{array}\right)\]Jacques Salomon Hadamard，1865～1963，法国数学家。巴黎高等师范学校博士，波尔多大学教授。他曾于1936年访华，执教于清华大学。中国偏微分方程研究事业的主要创始人之一——吴新谋教授，就是他的学生。
类似Hadamard product以及矩阵加法之类的操作，又被称为element-wise op或coefficient-wise op。
参考：
https://mp.weixin.qq.com/s/K_aNhzaxmchynDWTE1QFCQ
给你一些点与线，只用动画就能看懂张量乘法，还能证明迹循环定理
https://mp.weixin.qq.com/s/Mup0XmbGhunlkYl6Y95kiQ
丁玖：阿达马的数学、讨论班及中国情
张量分析
在同构的意义下，第零阶张量（r = 0）为标量（Scalar），第一阶张量（r = 1）为向量（Vector），第二阶张量（r = 2）则成为矩阵（Matrix）。
《张量分析》，黄克智著。
黄克智，1927年生，固体力学家。江西中正大学本科+清华硕士+莫斯科大学博士（因应召回国，放弃博士学位）。清华大学工程力学系教授、工程力学研究所所长，中国科学院院士。断裂力学领域权威。
参考：
https://www.zhihu.com/question/286175595
tensor contraction是什么?和内积有关系吗？
https://www.cnblogs.com/lywangjapan/p/12233140.html
张量网络学习笔记
https://www.cnblogs.com/lywangjapan/p/12041658.html
张量分解与应用-学习笔记（1）
https://www.cnblogs.com/lywangjapan/p/12068703.html
张量分解与应用-学习笔记（2）
https://www.cnblogs.com/lywangjapan/p/12089285.html
张量分解与应用-学习笔记（3）
三角矩阵的求逆问题
\[\begin{bmatrix} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33} \\ \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \\ \end{bmatrix}\]以3阶方阵为例，上面左边的矩阵被称为下三角矩阵（lower triangular matrix），而右边的矩阵被称为上三角矩阵（upper triangular matrix）。
对于矩阵求逆问题来说，下三角矩阵是一类比较简单的矩阵，求逆难度仅高于对角阵。
下三角矩阵的逆矩阵也是下三角矩阵，因此：
\[AA^{-1}=\begin{bmatrix} a_{11} & 0 & \dots & 0 \\ a_{21} & a_{22} & \dots & 0 \\ \dots & \dots & \dots & \dots \\ a_{n1} & a_{n2} & \dots & a_{nn} \\ \end{bmatrix} \begin{bmatrix} b_{11} & 0 & \dots & 0 \\ b_{21} & b_{22} & \dots & 0 \\ \dots & \dots & \dots & \dots \\ b_{n1} & b_{n2} & \dots & b_{nn} \\ \end{bmatrix} =\begin{bmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \dots & \dots & \dots & \dots \\ 0 & 0 & \dots & 1 \\ \end{bmatrix}\]由矩阵乘法定义，可得：
\[c_{ij}=\sum_{k=j}^ia_{ik}b_{kj}\]由\(c_{ij}=1,i=j\)，可得：\(b_{ii}=\frac{1}{a_{ii}}\)
由\(c_{ij}=0,i\neq j\)，可得：
\[c_{ij}=\sum_{k=j}^{i-1}a_{ik}b_{kj}+a_{ii}b_{ij}=0\]因此：
\[b_{ij}=-\frac{1}{a_{ii}}\sum_{k=j}^{i-1}a_{ik}b_{kj}=-b_{ii}\sum_{k=j}^{i-1}a_{ik}b_{kj}\]上三角矩阵求逆，可通过转置转换成下三角矩阵求逆。这里会用到以下性质:
\[(A^T)^{-1}=(A^{-1})^T\]LU分解
LU分解可将矩阵A分解为\(A=LU\)，其中L是下三角矩阵，U是上三角矩阵。
LU分解的用途很多，其中之一是求逆：
\[A^{-1}=(LU)^{-1}=U^{-1}L^{-1}\]LU分解有若干种算法，常见的包括Doolittle、Cholesky、Crout算法。
Myrick Hascall Doolittlee，1830~1913。
Andr´e-Louis Cholesky，1875~1918，法国数学家、工程师、军官。死于一战战场。Cholesky分解法又称平方根法，是当A为实对称正定矩阵时，LU三角分解法的变形。
Prescott Durand Crout，1907~1984，美国数学家，22岁获MIT博士。
您的打赏，是对我的鼓励
