• 随机变量的特征函数
• 概率分布（1）
  • 贝塔函数
  • 伽马函数
  • 排列组合
  • 伯努利试验
    • 二项分布
    • 几何分布
  • 二项分布的极限
  • 泊松分布
  • 贝塔分布和共轭先验分布
  • 多项分布和狄利克雷分布

随机变量的特征函数

特征函数（Characteristic function）是描述随机变量概率分布的重要工具，其定义如下。

设随机变量X的CDF为\(F_X(x)\)，则其特征函数定义为：

\[\varphi_X(t)=E(e^{itX})=\int_{-\infty}^{+\infty}e^{itx}\mathrm{d}F_X(x)\]

其中，\(i=\sqrt{-1}\)，并且

\[e^{itx}=\cos(tx)+i\sin(tx)\]

根据上述定义，\(\varphi_X(t)\)是\(F_X(x)\)的傅立叶变换。因此\(\varphi_X(t)\)和\(F_X(x)\)包含相同的信息，且是一一对应的。特别的，若X的PDF \(f_X(x)\)存在，则可通过傅立叶逆变换得到：

\[f_X(x)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}e^{-itx}\varphi_X(t)\mathrm{d}t\]

特征函数具有连续可微等良好的分析性质，因此对于那些矩母函数（Moment Generating Function，MGF）不存在的分布（如柯西分布和对数正态分布）很有用处。

特征函数本质上不是概率论的内容，而属于函数论的内容。不用傅立叶变换，用拉普拉斯变换、希尔伯特变换等等，也可能产生类似效果，当然具体结论会颇有不同。

概率分布（1）

进入正题之前，先介绍两个函数：贝塔函数和伽马函数。

贝塔函数

\[B(\alpha,\beta)=\int_{0}^{1}x^{\alpha-1}(1-x)^{\beta-1}dx\]

伽马函数

\[\Gamma(\theta)=\int_{0}^{\infty}x^{\theta-1}e^{-x}dx\]

http://cos.name/2013/01/lda-math-gamma-function/

神奇的Gamma函数

这篇文章对伽马函数的历史由来，讲的比较透彻。

简单来说，伽马函数就是阶乘算子在复数域的扩展。

伽马函数有以下一些性质：

\[\Gamma(x+1)=x\Gamma(x)\] \[\Gamma(n)=(n-1)!,n为整数\] \[{\Gamma(1-x)\Gamma(x)}=\frac{\pi}{\sin(\pi x)},x\in{(0,1)}\] \[\Gamma({1 \over 2})=\sqrt{\pi}\] \[B(m,n) = \frac{\Gamma(m)\Gamma(n)}{\Gamma(m+n)}\]

上式中的B函数，也就是现在的Beta函数。

对Gamma函数的定义做一个变形，就可以得到如下式子：

\[\int_0^{\infty} \frac{x^{\alpha-1}e^{-x}}{\Gamma(\alpha)}dx = 1\]

取积分中的函数作为概率密度，就得到一个形式最简单的Gamma分布的密度函数：

\[Gamma(x|\alpha) = \frac{x^{\alpha-1}e^{-x}}{\Gamma(\alpha)}\]

如果做一个变换\(x=\beta t\)，就得到Gamma分布的更一般的形式：

\[Gamma(t|\alpha, \beta) = \frac{\beta^\alpha t^{\alpha-1}e^{-\beta t}}{\Gamma(\alpha)}\]

其中\(\alpha\)称为shape parameter，主要决定了分布曲线的形状; 而\(\beta\)称为rate parameter或者inverse scale parameter(\(1/\beta\)称为scale parameter)，主要决定曲线有多陡。

参考：

http://blog.csdn.net/u010945683/article/details/48950063

贝塔、伽马分布

排列组合

排列组合是高中数学的内容，这里仅列出公式，以备参考。

\[P^m_n=\frac{n!}{(n-m)!}\] \[C^m_n=\frac{P^m_n}{m!}=\frac{n!}{m!(n-m)!}\]

\(C^m_n\)有时也被记作\(\binom{n}{m}\)，注意这两种表示法的上下标的顺序。

伯努利试验

伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验。其特点是该随机试验只有两种可能结果：发生或者不发生。然后我们假设该项试验独立重复地进行了n次，那么我们就称这一系列重复独立的随机试验为n重伯努利试验，或称为伯努利概型。

n重伯努利试验导出了两个重要的分布。

二项分布

n重伯努利试验中，事件A发生K次的概率是：

\[\Pr(X = k) = \binom n k p^k(1-p)^{n-k}\]

其中，p为单次试验中，事件A发生的概率。

这种分布，被称为二项分布（Binomial Distribution）。特别的，当n=1时，被称为伯努利分布。

几何分布

几何分布（Geometric distribution）有两个定义：

1.在n重伯努利试验中，试验k次才得到第一次成功的概率：

\[\Pr(X = k) = (1-p)^{k-1}\,p\,\]

1.在n重伯努利试验中，第一次成功之前，失败k次的概率：

\[\Pr(Y=k) = (1 - p)^k\,p\,\]

显然\(Y=X-1\)。

二项分布的极限

二项分布实际上有两个极限分布。

如上所述，二项分布有两个参数n和p。

如果p为定值，\(n\to\infty\)，则极限分布为正态分布。正态分布的性质参见《图像处理理论（二）》。

如果\(p\to 0,n\to\infty\)，则极限分布为泊松分布（Poisson distribution）。

泊松分布

泊松分布有两个定义：

定义一：一个随机变量X, 只能取值非负整数（x=0,1,2,…），且相应的概率为\(e^{-\lambda }\frac{\lambda ^x}{x!}\)，则称该变量服从poisson分布。

定义二：假定一个事件在一段时间内随机发生，且符合以下条件：

（1）将该时间段无限分隔成若干个小的时间段，在这个接近于零的小时间段里，该事件发生一次的概率与这个极小时间段的长度成正比。

（2）在每一个极小时间段内，该事件发生两次及以上的概率恒等于零。

（3）该事件在不同的小时间段里，发生与否相互独立。

则该事件称为poisson process。

比如，一段时间t内，电话交换站收到的呼叫次数k，就是泊松分布的。很显然，呼叫次数和时间是有关系的，时间越长，呼叫次数越多。反之，\(t\to 0\)，则\(k\to 0\)。这正好符合二项分布的泊松极限的定义。

泊松分布的独特之处，还在于它的两个要素t和k，一个是连续型随机变量，另一个是离散型随机变量。无形之中，它成为了这两类变量之间的桥梁。与此相关的数学分支，一般被称为泊松分析。

仍以上面的例子为例，如果反过来，求两次来电的时间间隔t，则t符合指数分布。

参考：

https://www.zhihu.com/question/26441147

泊松分布的现实意义是什么，为什么现实生活多数服从于泊松分布？

http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html

泊松分布和指数分布：10分钟教程

http://blog.csdn.net/kicilove/article/details/78655856

数据科学家应知必会的6种常见概率分布

https://mp.weixin.qq.com/s/PIKvYvXd9PaVHFi_I0U4cw

一文读懂泊松分布，指数分布和伽马分布

https://mp.weixin.qq.com/s/BySEOOgPpTispZi_XBER4w

Poisson过程

贝塔分布和共轭先验分布

\[f(x;\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}\]

贝塔分布的PDF（probability density function）和CDF（cumulative distribution function）如下图所示：

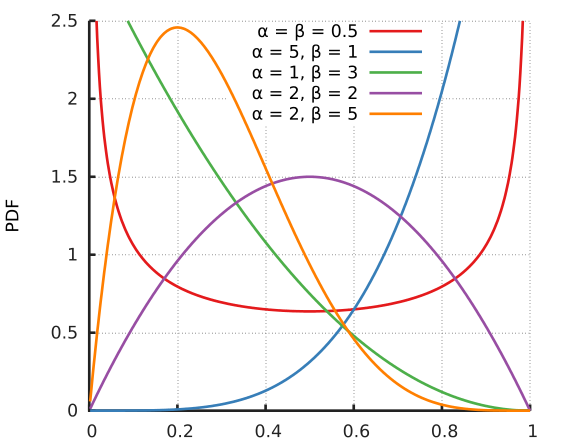
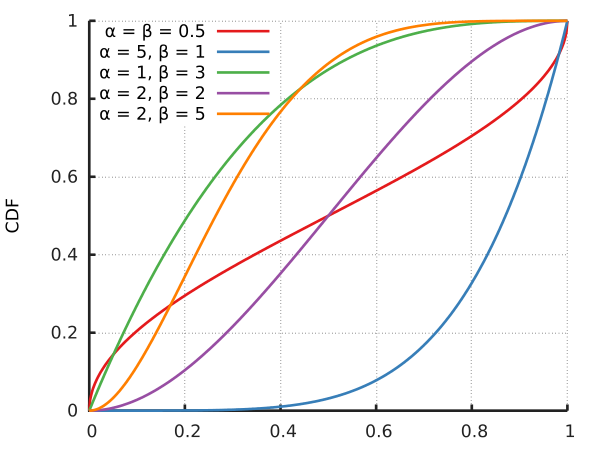
从上图可以看出它是个百变星君，它可以是凹的、凸的、单调上升的、单调下降的；可以是曲线也可以是直线。由于Beta分布能够拟合如此之多的形状，因此它在统计数据拟合中，被广泛使用。

下面来讲一下Beta分布的推导，并引出共轭先验分布的概念。

设一事件A的概率\(p(A)=\theta\)，为了估计\(\theta\)的值，作了n次独立观察，其中事件A出现的次数为X。显然X服从二项分布\(X\sim B(n,\theta)\)。

因此：

\[p(X=x\mid \theta)= \binom{n}{x}\theta^{x}(1-\theta)^{n-x}\]

利用贝叶斯公式，我们首先需要确定先验概率\(p(\theta)\)。在未得到其余信息前，我们只能认为\(\theta\)在(0,1)上均匀分布（即\(\theta\sim Uniform(0,1)\)），这是一种不失偏颇的先验估计。

则联合概率分布为：

\[p(x,\theta)=p(x\mid \theta)p(\theta)\]

边缘概率分布：

\[\begin{align}p(x)&=\int_{0}^{1}p(x,\theta)d\theta=\int_{0}^{1}\binom{n}{x}\theta^{x}(1-\theta)^{n-x}d\theta\\ &=\binom{n}{x}B(x+1,n-x+1)=\binom{n}{x}\frac{\Gamma(x+1)\Gamma(n-x+1)}{\Gamma(n+2)}\end{align}\]

综合以上，可得\(\theta\)的后验分布:

\[p(\theta\mid x)=\frac{p(x,\theta)}{p(x)}=\frac{\theta^{(x+1)-1}(1-\theta)^{(n-x+1)-1}}{B(x+1,n-x+1)}\]

因此：\(\theta \mid x\sim Beta(x+1,n-x+1)\)

考虑到\(Uniform(0,1)=Beta(1,1)\)，因此在这个例子中，先验分布和后验分布，实际上是同一类型的分布。这种情况被称为共轭先验分布。

上述过程的形式化描述为：

\[Uniform(\theta)+B(n,\theta)\to Beta(x+1,n-x+1)\]

即

\[先验参数分布+数据分布\to 后验分布\]

定义：设\(\theta\)是某分布中的一个参数，\(\pi(\theta)\)是其先验分布。假如由抽样信息算得的后验分布\(\pi(\theta \mid x)\)与\(\pi(\theta)\)同属于一个分布族，则称\(\pi(\theta)\)是\(\theta\)的共轭先验分布。

从这个定义可以看出，共轭先验分布是对某一分布中的参数而言的，离开指定参数及其所在的分布，谈论共轭先验分布是没有意义的。

常见的共轭先验分布：

总体分布	参数	共轭先验分布
二项分布	成功概率	贝塔分布
泊松分布	均值	伽马分布
指数分布	均值倒数	伽马分布
正态分布（方差已知）	均值	正态分布
正态分布（方差未知）	方差	倒伽马分布

共轭先验分布中，由于先验分布和后验分布都是同一个分布族，因此有利于简化计算。同时，先验参数往往会传递到后验分布，这样就能够比较方便的确定参数的实际意义。

参考：

http://blog.csdn.net/u010945683/article/details/49149815

共轭先验分布

https://mp.weixin.qq.com/s/B-yvH8ecirsROfYZ5CcZjg

一文读懂正态分布与贝塔分布

https://mp.weixin.qq.com/s/4uia4ijUUaumc2PNvCEWiw

“共轭分布”是什么？

多项分布和狄利克雷分布

伯努利试验只有两个可能的实验结果，如果实验结果的个数超过2个，那么二项分布就变成了多项分布（multinomial distribution）：

\[f(x_1,\ldots,x_k;n,p_1,\ldots,p_k)=\frac{n!}{x_1!\cdots x_k!} p_1^{x_1} \cdots p_k^{x_k}\]

多项分布对应的共轭先验分布是狄利克雷分布（Dirichlet distribution）：

\[f \left(x_1,\cdots, x_{K}; \alpha_1,\cdots, \alpha_K \right) = \frac{1}{\mathrm{B}(\boldsymbol\alpha)} \prod_{i=1}^K x_i^{\alpha_i - 1}\tag{1}\]

这里引入向量表示的贝塔函数：

\[\mathrm{B}(\boldsymbol\alpha) = \frac{\prod_{i=1}^K \Gamma(\alpha_i)}{\Gamma\left(\sum_{i=1}^K \alpha_i\right)},\qquad\boldsymbol{\alpha}=(\alpha_1,\cdots,\alpha_K)\]

狄利克雷分布的密度函数如下所示(3维)：

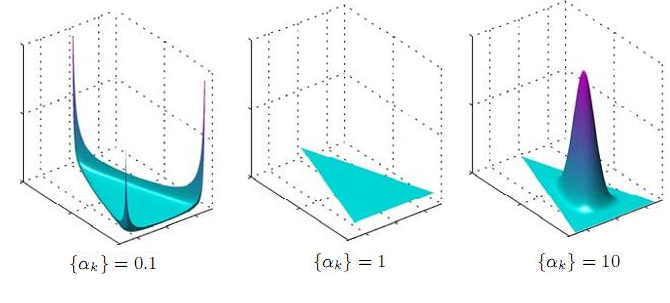
上面的图，实际上是个4维图，只不过用一个平面上的三角形代表实验结果的3维而已。这也是一种高维数据可视化的方法。