graphics » 图像处理理论(二)——滤波基础, 形态学, 边缘检测
2016-06-30 :: 6523 Words- 二值化(续)
- 方框滤波(Box Filter)
- 高斯滤波(Gauss filter)
- 二维高斯滤波
- 高斯积分
- 中值滤波(Median filter)
- 膨胀与腐蚀(Dilation & Erosion)
- 高级形态学操作
- 边缘检测
二值化(续)
一维交叉熵值法
对于两个分布R和Q,定义其信息交叉熵D如下:
\[R=\{r_1,r_2,\dots,r_n\},Q=\{q_1,q_2,\dots,q_n\}\] \[D(Q,R)=\sum_{k=1}^{n}q_k log_2\frac{q_k}{r_k}\]严格来说,这里定义的是相对熵(relative entropy),又称为KL散度(Kullback-Leibler divergence)或KL距离,是两个随机分布间距离的度量。从公式可以看出,KL距离和经典概率论中的二项分布有很密切的关系。
交叉熵的严格定义参见:
https://en.wikipedia.org/wiki/Cross_entropy
http://www.voidcn.com/blog/rtygbwwwerr/article/p-5047519.html
交叉熵(Cross-Entropy)
二值化过程实际上就是从分布\(R=\{r_1,r_2,\dots,r_L\}\)到分布\(Q=\{q_A,q_B\}\)的过程。
因此
\[D(t)=\sum_{i=0}^{t}ip_i log_2(\frac{p_i}{\omega_A})+\sum_{i=t+1}^{L-1}ip_i log_2(\frac{p_i}{\omega_B})\]其中,使得D最小的t即为最小交叉熵意义下的最优阈值。
二维Otsu法
Otsu法对噪音和目标大小十分敏感,它仅对类间方差为单峰的图像产生较好的分割效果。
当目标与背景的大小比例悬殊时,类间方差准则函数可能呈现双峰或多峰,此时效果不好,但是Otsu法是用时最少的。
二维Otsu法,在考虑像素点灰度级p的基础上,增加了对像素点邻域平均像素值s的考虑。
如果p比s大很多,说明像素的灰度值远远大于其临域的灰度均值,故而该点很可能是噪声点,反之如果p比s小很多,即该点的像素值比其临域均值小很多,则说明是一个边缘点。这两种点在后续的计算中,都要去除掉。
二维Otsu法的推导过程极为复杂,可参见:
http://blog.csdn.net/likezhaobin/article/details/6915755
灰度图像阈值化分割常见方法总结及VC实现
参考
https://mp.weixin.qq.com/s/xCmagMDmcPRf3xAkOMT4rw
视觉与图像:阈值分割
https://mp.weixin.qq.com/s/Us7K5SBLltJIKzaJZQqltw
简单粗暴二分类分割方法Riddler-Calvard详解
https://mp.weixin.qq.com/s/gylWAKk4q0UNlhxIXrFHkQ
基于OpenCV的图像阈值分割处理
方框滤波(Box Filter)
当normalize=true时的方框滤波,也被称为均值滤波(Mean filter)。
高斯滤波(Gauss filter)
高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。
正态分布的概率密度函数为:
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]其标准化后的概率密度函数为:
\[f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\]标准二维正态分布的概率密度函数为:
\[f(x,y)=\frac{1}{2\pi}e^{-\frac{x^2+y^2}{2}}=f(x)f(y)\]这个公式表明标准二维正态分布,可以分解为两个正交方向上的标准一维正态分布。也就是说标准二维正态分布不仅是中心对称,也是轴对称的。
正态分布的性质:
1.两个正态分布密度的乘积、卷积,还是正态分布。
2.正态分布的傅立叶变换、共轭分布,还是正态分布。
3.正态分布和其它具有相同均值、方差的概率分布相比,具有最大熵。
4.二项分布、泊松分布、\(\chi^2\)分布、t分布等在样本增大的情况下,都趋向于正态分布。
正态分布的相关内容可参考:
标准正态分布的最佳逼近符合杨辉三角,比如一个具有5个点的一维标准正态分布的最佳逼近为:
\[\left[ \begin{array}{ccccc} 1&4&6&4&1\end{array} \right]\]同理,最常用的3*3高斯滤波h矩阵为:
\[\left[\begin{array}{c} 1\\2\\1\end{array} \right]\times \left[\begin{array}{ccc} 1&2&1\end{array} \right]=\left[\begin{array}{ccc} 1&2&1\\ 2&4&2 \\ 1&2&1\end{array} \right]\]其归一化形式为:
\[\left[\begin{array}{ccc} 0.0625&0.125&0.0625\\ 0.125&0.25&0.125 \\ 0.0625&0.125&0.0625\end{array}\right]\]从效果来说,高斯滤波可产生类似毛玻璃的效果。
参考:
https://mp.weixin.qq.com/s/pJhfdLZxcKTI30xzbU2UoA
5分钟让你看懂高斯模糊算法
https://mp.weixin.qq.com/s/V8zMnADGHW_owfMPDtXvgQ
如何让8岁表妹学会正态分布
https://mp.weixin.qq.com/s/q252Lc0Wl5uNc8-tw9nlgw
高中就开始学的正态分布,原来如此重要
https://mp.weixin.qq.com/s/KYxUoaz4dlheFLz3ZinB2w
十种图像模糊算法的总结与实现
https://mp.weixin.qq.com/s/6PQt-XcxdYJwIItf2RNuBg
图像平滑之均值滤波、方框滤波、高斯滤波及中值滤波
https://mp.weixin.qq.com/s/6-JK8HA40Q0FQNUkB62Fug
一个简单方法识别毛玻璃、高斯模糊
二维高斯滤波
由标准二维正态分布的正交性,可知二维高斯滤波实际上可以分解为x、y两个方向上的一维高斯滤波。当然,这时候的kernel的尺寸不再是方形的,而是1*n的长条形。
这是一项有用的特性,因为这样只需要\(O(n \times M \times N)+O(m \times M \times N)\)次运算,而直接使用二维高斯滤波的计算量为\(O(m \times n \times M \times N)\)。其中m,n,M,N分别是kernel和图像的长、宽。
高斯积分
\[\int_{-\infty}^\infty e^{-x^2}\mathrm{d}x=\sqrt{\pi}\]中值滤波(Median filter)
中值滤波是一种典型的非线性滤波技术,对于斑点噪声(speckle noise)和椒盐噪声(salt-and-pepper noise)来说尤其有用,对滤除脉冲干扰及图像扫描噪声非常有效,也常用于保护边缘信息。
以3*3的滤波窗口为例,计算以点\([i,j]\)为中心的像素中值步骤如下:
1)对\(U^+(A,1)\)的9个像素点\(a_0\sim a_8\),按强度值大小排列像素点,得到有序数组\(A_0\sim A_8\)
2)选择排序像素集的中间值\(A_4\)作为点\([i,j]\)的新值。
从效果来说,中值滤波可产生类似油彩画的效果。
上面这些滤波的效果如图所示:

膨胀与腐蚀(Dilation & Erosion)
腐蚀和膨胀是对白色部分(高亮部分)而言的,不是黑色部分。膨胀就是图像中的高亮部分进行膨胀,“领域扩张”,效果图拥有比原图更大的高亮区域。腐蚀就是原图中的高亮部分被腐蚀,“领域被蚕食”,效果图拥有比原图更小的高亮区域。
具体方法如下:
1.膨胀。
\[g(i,j)=max_{k,l}f(i,j)\]2.腐蚀。
\[g(i,j)=min_{k,l}f(i,j)\]这里仿照C语言的记法,将膨胀操作记为\(dilate(src)\),其中src表示源图像。同理,将腐蚀操作记为\(erode(src)\)。
效果如下:

膨胀和腐蚀不仅是基本的形态学操作,而且也是一种滤波器。它们和中值滤波一样,都是百分比(percentile)滤波的特例。当百分比为100%时,为最大值滤波,即膨胀操作;当百分比为0%时,为最小值滤波,即腐蚀操作;当百分比为50%时,即为中值滤波。
高级形态学操作
1.开运算(Opening Operation)
\[open(src)=dilate(erode(src))\]开运算可以用来消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。
2.闭运算(Closing Operation)
\[close(src)=erode(dilate(src))\]闭运算能够排除小型黑洞(黑色区域)。
3.形态学梯度(Morphological Gradient)
\[morphgrad(src)=dilate(src)-erode(src)\]对二值图像进行这一操作可以将团块(blob)的边缘突出出来。我们可以用形态学梯度来保留物体的边缘轮廓。
4.顶帽(Top Hat)
\[tophat(src)=src-open(src)\]顶帽运算往往用来分离比邻近点亮一些的斑块。当一幅图像具有大幅的背景的时候,而微小物品比较有规律的情况下,可以使用顶帽运算进行背景提取。
5.黑帽(Black Hat)
\[blackhat(src)=close(src)-src\]黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域。
效果如下:
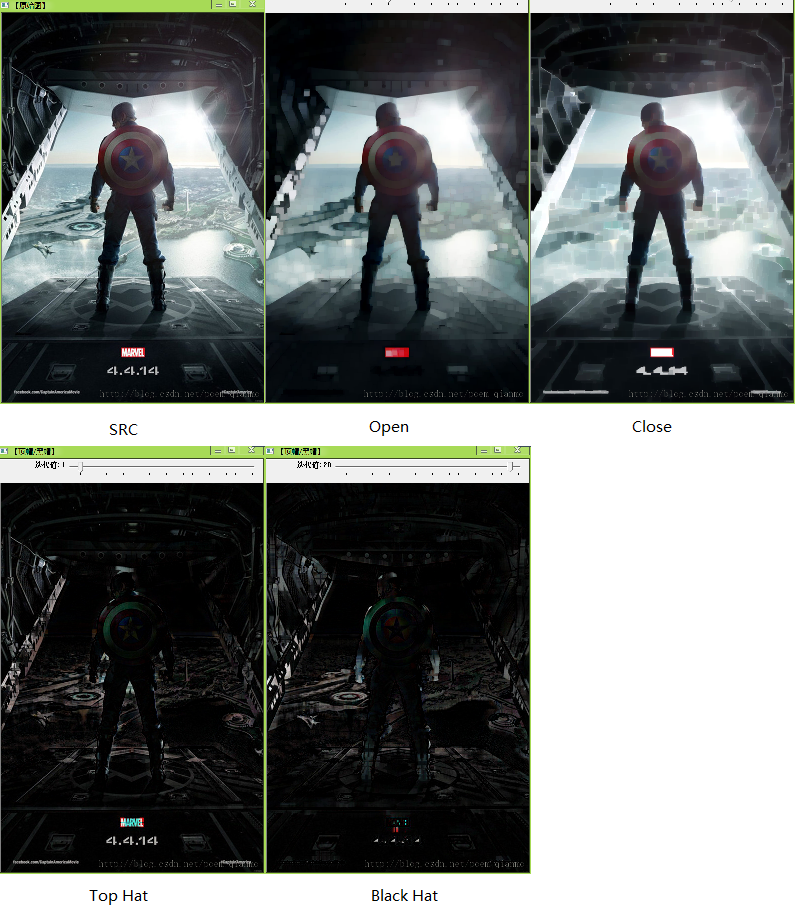
边缘检测
梯度
从数学概念上来说,一维梯度G,实际上就是函数的斜率,也就是一阶导数。二维梯度G是个向量,一般用两个维度上的偏导数\(G_x\)和\(G_y\)来刻画,即\(G=[G_x,G_y]\)。显然,沿梯度向量方向,函数值增加最快。
梯度向量求模的常见方法有:
\[G=\mid G_x\mid +\mid G_y\mid (模1)\] \[G=\sqrt{G_x^2+G_y^2}(模2)\] \[G=max(\mid G_x\mid ,\mid G_y\mid )(模\infty)\]显然,梯度的模大的点,有很大可能是边缘点。常用的梯度算子有Roberts算子、Sobel算子和Prewitt算子。
Roberts算子
\[s_x=\left[\begin{array}{cc} 1&0\\ 0&-1\end{array} \right],s_y=\left[\begin{array}{cc} 0&-1\\ 1&0\end{array} \right]\] \[G(i,j)=\mid s_x\otimes f\mid +\mid s_y\otimes f\mid\] \[=\mid f(i,j)-f(i+1,j+1)\mid +\mid f(i+1,j)-f(i,j-1)\mid\]以下将\(s_x\otimes f\)简记做\(G_x\)。
Sobel算子
\[s_x=\left[\begin{array}{ccc} -1&0&1\\ -2&0&2 \\ -1&0&1\end{array} \right],s_y=\left[\begin{array}{ccc} 1&2&1\\ 0&0&0 \\ -1&-2&-1\end{array} \right]\] \[G=\sqrt{G_x^2+G_y^2}\] \[梯度方向\theta=arctan(\frac{G_y}{G_x})\]Prewitt算子
\[s_x=\left[\begin{array}{ccc} -1&0&1\\ -1&0&1 \\ -1&0&1\end{array} \right],s_y=\left[\begin{array}{ccc} 1&1&1\\ 0&0&0 \\ -1&-1&-1\end{array} \right]\]其他与Sobel算子相同。
拉普拉斯算子
拉普拉斯算子是一种二阶微分算子,因此,它一般用二阶微分符号\(\nabla^2f\)来表示。其常用的相关核有:
\[h_1=\left[\begin{array}{ccc} 0&-1&0\\ -1&4&-1 \\ 0&-1&0\end{array} \right],h_2=\left[\begin{array}{ccc} -1&-1&-1\\ -1&8&-1 \\ -1&-1&-1\end{array} \right]\]从中可以看出,拉普拉斯算子的相关核有以下特点:
1.各元素中心对称。
2.中心元素为正值。(在有些课本中,中心元素也可为负值,但相关公式就需要做相应的符号上的修改。在本教程中,中心元素一律为正值。)
3.所有元素的和为0。
拉普拉斯算子和正态分布有很大关联,也有标准差\(\sigma\)的概念。一般来说,中心元素的值越大,\(\sigma\)越小。算子对图像的模糊(或锐化)程度与\(\sigma\)成正比。
对称梯度算子
\[s_x=\left[\begin{array}{ccc} -1&0&1\\ -d&0&d \\ -1&0&1\end{array} \right],s_y=\left[\begin{array}{ccc} 1&d&1\\ 0&0&0 \\ -1&-d&-1\end{array} \right]\]可以看出Sobel算子\((d=2)\)和Prewitt算子\((d=1)\),都是对称梯度算子的特例。d的常用值还有\(\sqrt{2}\)。

您的打赏,是对我的鼓励
