graphics » 图像处理理论(四)——Schmid滤波, HOG, Haar, SIFT
2017-08-23 :: 5488 WordsGabor滤波
Gabor filter(续)
\(\lambda\):正弦函数波长;\(\theta\):Gabor核函数的方向;\(\psi\):相位偏移;\(\sigma\):高斯函数的标准差;\(\gamma\): 空间的宽高比。
可以看出Gabor filter是一个复函数,其实部为:
\[g(x,y;\lambda,\theta,\psi,\sigma,\gamma)=\exp\left(-\frac{x'^2+\gamma^2y'^2}{2\sigma^2}\right)\cos\left(2\pi\frac{x'}{\lambda}+\psi\right)\]其虚部为:
\[g(x,y;\lambda,\theta,\psi,\sigma,\gamma)=\exp\left(-\frac{x'^2+\gamma^2y'^2}{2\sigma^2}\right)\sin\left(2\pi\frac{x'}{\lambda}+\psi\right)\]此外,还有对数Gabor函数:
\[G(f)=\exp\left(\frac{-(log(f/f_0))^2}{2(log(\sigma/f_0))^2}\right)\]Gabor滤波的效果
参考文献3,给出了Gabor滤波的效果图,如下所示:

图1
从效果来看,该滤波可获得美术上的浮雕效果。但实际上,大多数的边缘检测算法都可得到类似效果,这并不是Gabor滤波的主流用法。
以下对参考文献3做一个补充说明:
1.Gabor滤波是复数域的,这点和之前提到的滤波算法有很大的不同。因此,Gabor滤波计算核的方法有3种:复数、实部和虚部。参考文献3采用的是实部法。1987年,J.P. Jones和L.A. Palmer发现Gabor变换所采用的核(Kernels)的实部与哺乳动物视觉皮层简单细胞2D感受野剖面(Profile)非常相似。
2.实部计算的结果有正有负。参考文献3给出的归一化算法,很有通用性,摘录如下:
\[G(x,y)=\frac{(f(x,y)-min(F))*D}{max(F)-min(F)}\]其中,F为源图像所有像素的集合,D为总的灰度级数。
Gabor滤波采样方式与图像压缩
Gabor滤波和之前的滤波算法的另一大差异是:Gabor滤波核不是一个,而是由若干不同参数组合而成的一组核,其中的每一个参数组合被称为一个采样点。
从Gabor filter的计算公式亦可看出,组成采样点的参数,既有时空域参数,也有频域参数。这些采样点在时空域和频域中如何分布,才能达到最终效果呢?
由于Gabor filter不是正交基,因此针对采样点分布提出了Tight Frame的概念。参考文献1给出了满足Tight Frame要求的采样点分布方式(简称采样方式)的条件。这里的推导非常复杂,但从概念上可以类比信号处理中的奈奎斯特采样定理。
Tight Frame有个重要特性:
如果采样方式满足Tight Frame条件,且\(图像集B=Gabor(图像A),图像C=Gabor^{-1}(图像集B)\),那么\(图像A\approx 图像C\)。其中的\(Gabor\)和\(Gabor^{-1}\)分别表示Gabor变换及其逆变换。
参考文献2给出了采用上述方法对Lena图进行压缩并还原的例子。这也是Gabor滤波在图像处理领域的早期典型应用。
Gabor滤波与模式识别

图2
2000年以后,科学界对Gabor滤波的研究,主要集中在模式识别方面。比如图2就是参考文献4中给出的人脸识别方面的Gabor滤波效果图。其中,左边是原图,而右边是40组不同参数的Gabor滤波器所得到的滤波效果图。
1幅原图变成40幅滤波效果图的过程,在数学上是个升维过程。在后处理阶段为了处理的方便,往往会进行数据降维,如参考文献5所示。
从中还可以看出,虽然图1显示出一定的艺术处理效果,但大多数情况下,Gabor滤波所得的图像是如图2所示的极度扭曲而无明显意义的图片。Gabor滤波的真正用途,并不是给人看,而是给机器看。
从上面的讨论可知,Gabor滤波是一种带通滤波,使用不同的时空域或频域参数,可以过滤出不同的时空域或频域特征。这些特征正是模式识别所需要的。

图3
图3是参考文献4给出的一种Gabor滤波器的使用场景图,从中可以看出Gabor滤波效果图是如何应用到人脸识别技术中的。
必须指出的是:Gabor滤波效果图的后处理方法有很多种,而图3仅是其中一种而已。
参考
1.1996年IEEE论文:《Image Representation Using 2D Gabor Wavelets》
作者:Tai Sing Lee,哈佛大学博士,卡内基梅隆大学教授。
2.1988年IEEE论文:《Complete Discrete 2-D Gabor Transforms by Neural Networks for Image Analysis and Compression》
作者:JohnG. Daugman,哈佛大学博士,剑桥大学教授。
3.http://blog.csdn.net/xiaowei_cqu/article/details/24745945
Gabor滤波器
4.《Face recognition using Ada-Boosted Gabor features》
作者:Peng Yang,Shiguang Shan,Wen Gao,Stan Z. Li,Dong Zhang,中科院计算所和微软亚洲研究院的几个小牛。
高文,1956年生,哈尔滨工业大学博士(1988)+东京大学博士(1991)。中科院计算所所长,中国工程院院士。
山世光,1975年生,哈尔滨工业大学本硕(1997,1999)+中科院博士(2004)。中科视拓CEO。
5.http://www.cnblogs.com/Jack-Lee/p/3649114.html
基于OpenCV的Gabor变换及特征提取
https://mp.weixin.qq.com/s/RS0Zw6iLFQBUlpOdkuoFbg
从傅立叶变换到Gabor滤波器
https://mp.weixin.qq.com/s/UDJAYB79KaPB0pgnnCIPTw
不确定性原理的前世今生
https://blog.csdn.net/jbb0523/article/details/42028587
从傅立叶(Fourier)变换到伽柏(Gabor)变换再到小波(Wavelet)变换
https://mp.weixin.qq.com/s/U96qNphaZOPQJj97xexluw
让机器“看见”:图像数据的特征提取方法
https://mp.weixin.qq.com/s/pR9mKpSjdObkNWHrkezPcw
简简单单用OpenCV让一只小猫咪变成奶凶奶凶的科技猫
Schmid滤波
Schmid滤波器是一种类Gabor滤波器。其计算公式为:
\[F(r,\sigma,\tau)=\frac{1}{Z}\cos\left(\frac{2\pi\tau r}{\sigma}\right)e^{-\frac{r^2}{2\sigma^2}}\]下图是Schmid滤波器和Gabor滤波器的“核”图像。“核”图像是滤波器“核”函数的图像化展示。

其中,前13个是Schmid滤波器,后8个是Gabor滤波器。“核”图像中的白色部分,实际上就是该滤波器的带通部分。
从中可以看出,Gabor滤波器有方向性,而Schmid滤波器是各向同性的环状滤波。
参考
2010年IEEE论文:《Constructing models for content-based image retrieval》
作者:Cordelia Schmid,女,卡尔斯鲁厄理工学院博士。现在INRIA(法国国家信息与自动化研究所)从事研究工作。
HOG
Histogram of oriented gradients是一种用于物体检测的算子。

HOG的计算步骤,如上图所示:
1.首先将图像均匀的分为若干个区域。这样的区域一般叫做Bin或Cell。
2.计算一个Cell中每个像素的梯度值。
3.将梯度值分为若干个区间,统计一个Cell中落在该区间的像素的个数,以得到直方图。
将整幅图所有Cell的HOG交给SVM或者AdaBoost之类的分类器,以获得待识别物体的HOG特征。
参考:
https://mp.weixin.qq.com/s/1l1OU81-BDlvyLZo6eM-4g
方向梯度直方图
https://buptldy.github.io/2016/03/31/2016-03-31-HOG%20Note/
《Histograms of Oriented Gradients for Human Detection》Note
https://mp.weixin.qq.com/s/9345Y-Ag-2AWPur-NAdiEw
HOG特征详解与行人检测
https://mp.weixin.qq.com/s/eRyCrvZGjsd9ZQ_NbNwB3w
梯度直方图(HOG)用于图像多分类和图像推荐
Haar
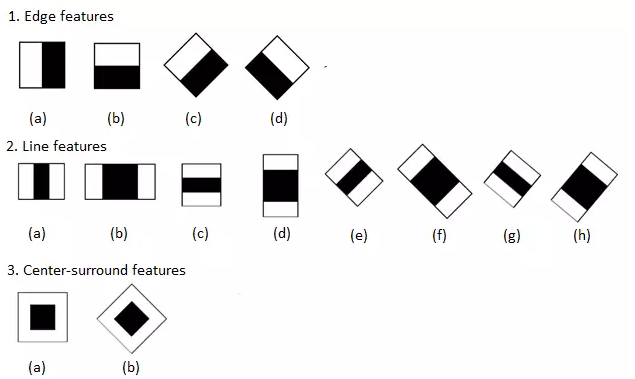
Haar特征本身并不复杂,就是用图中黑色矩形区域内所有像素值的和减去白色矩形区域内所有像素值的和,得到的值称为Haar特征值。
同样的,将整幅图所有Cell的Haar特征值交给SVM或者AdaBoost之类的分类器,就得到了待识别物体的Haar特征。
这也是2010年前后人脸识别/车牌识别的标准做法,OpenCV在v4以前的识别算法就是基于这套算法。
从上面的描述可以看出:早期的算子主要从信号处理的角度出发,而HOG和Haar开始考虑使用统计学方法提取有效特征。这也是90年代后期,统计学被引入CV界的直接结果。
Alfréd Haar,1885~1933,匈牙利数学家。哥廷根大学博士,导师是David Hilbert。Franz Joseph University教授。
Franz Joseph University是一所现在已经不存在的大学,有“小哥廷根”的称号,因为这里的数学系有大量的哥廷根大学毕业生执教。大学所在地Kolozsvár,在二战前后,一会儿归罗马尼亚,一会归匈牙利。当1945年,罗马尼亚最终接管该地之后,将学校的校舍分给了一所罗马尼亚大学,而将学校教师迁往别处,另建了一所大学。
吐槽一下,罗马尼亚主动投靠元首,却弄的割地予人,实在是太讽刺了。
当然这样做,自然有元首的考量。匈牙利更早投靠元首,和元首关系也更铁,所以拉架的时候,自然更偏匈牙利一些。况且,元首还许诺占了苏联土地,可以补偿罗马尼亚一些。反之,慈父也是一样的路数。罗马尼亚倒戈之后,参加了布达佩斯战役,有些功劳。而且苏联占了罗马尼亚的土地,也需要给它个补偿。
PS:记得10年前在学校读书的时候,CV还从属于信号处理专业。但以今日的角度来看,恐怕从属于CS专业,似乎更合适一点。从招聘信息看,现在的CV工作,已经很少提及信号处理的能力了。
参考:
http://www.cnblogs.com/ello/archive/2012/04/28/2475419.html
浅析人脸检测之Haar分类器方法
https://mp.weixin.qq.com/s/g-F-D5PC75BjbaRBmifnZw
人脸Haar特征与快速计算神器:积分图
https://mp.weixin.qq.com/s/0yaBwb_HZQXV27ep87ch_A
基于Adaboost算法的人脸检测分类器!
SIFT
概述
SIFT算法是CV领域在进入DL时代之前的20年中,最重要的成果。
尺度不变特征转换(Scale-invariant feature transform或SIFT)是一种电脑视觉的算法用来侦测与描述影像中的局部性特征,它在尺度空间中寻找极值点,并提取出其位置、尺度、旋转不变量,此算法由David Lowe在1999年所发表,2004年完善总结。
David G. Lowe,英属不列颠哥伦比亚大学(UBC)本科+斯坦福博士(1985)。UBC教授,Google资深科学家。
个人主页:
http://www.cs.ubc.ca/~lowe/
他在个人主页中提供了一份CV界知名的公司或研究机构的名单:
http://www.cs.ubc.ca/~lowe/vision.html
尺度空间
尺度空间(scale space)思想最早是由Iijima于1962年提出的,后经witkin和Koenderink等人的推广逐渐得到关注,在计算机视觉领域使用广泛。
尺度空间理论的基本思想是:在图像信息处理模型中引入一个被视为尺度的参数,通过连续变化尺度参数获得多尺度下的尺度空间表示序列,对这些序列进行尺度空间主轮廓的提取,并以该主轮廓作为一种特征向量,实现边缘、角点检测和不同分辨率上的特征提取等。

您的打赏,是对我的鼓励
