• Harris
  • Harris Corner Detector（续）
  • Harris角点的性质
  • 参考
• Optical flow
  • 基本概念
  • 光流约束方程
  • 参考
• TLD
• ORB
  • 背景提取

Harris

Harris Corner Detector（续）

其中：

\[M(x,y)=\sum_w \begin{bmatrix}I_x(x,y)^2&I_x(x,y)I_y(x,y) \\ I_x(x,y)I_y(x,y)&I_y(x,y)^2\end{bmatrix} = \begin{bmatrix}\sum_w I_x(x,y)^2&\sum_w I_x(x,y)I_y(x,y) \\\sum_w I_x(x,y)I_y(x,y)&\sum_w I_y(x,y)^2\end{bmatrix}=\begin{bmatrix}A&C\\C&B\end{bmatrix}\]

即：

\[c(x,y;\Delta x,\Delta y)\approx A\Delta x^2+2C\Delta x\Delta y+B\Delta y^2\]

其中：

\[A=\sum_w I_x^2, B=\sum_w I_y^2,C=\sum_w I_x I_y\]

二次项函数本质上就是一个椭圆函数。椭圆的扁率和尺寸是由M(x,y)的特征值\(\lambda_1, \lambda_2\)决定的，轴向是由M(x,y)的特征矢量决定的，如下图所示，椭圆方程为：

\[[\Delta x,\Delta y]M(x,y)\begin{bmatrix}\Delta x \\ \Delta y\end{bmatrix} = 1\]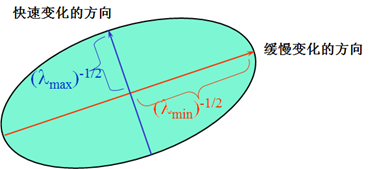

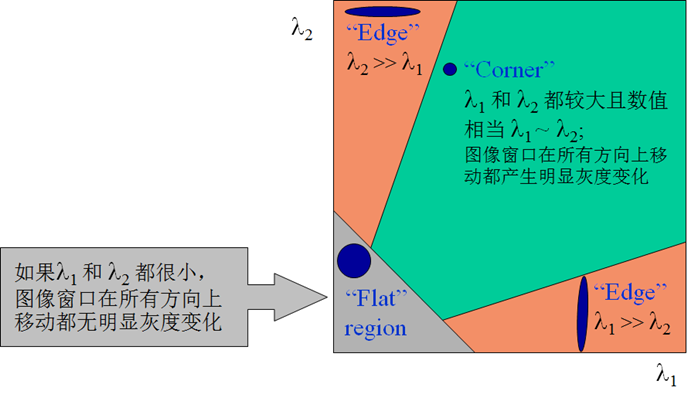
椭圆函数特征值与图像中的角点、直线（边缘）和平面之间的关系如下图所示。共可分为三种情况：

图像中的直线。一个特征值大，另一个特征值小，\(\lambda_1\gg \lambda_2\)或\(\lambda_2\gg \lambda_1\)。自相关函数值在某一方向上大，在其他方向上小。

图像中的平面。两个特征值都小，且近似相等；自相关函数数值在各个方向上都小。

图像中的角点。两个特征值都大，且近似相等，自相关函数在所有方向都增大。

根据二次项函数特征值的计算公式，我们可以求M(x,y)矩阵的特征值。但是Harris给出的角点差别方法并不需要计算具体的特征值，而是计算一个角点响应值R来判断角点。R的计算公式为：

\[R=det \boldsymbol{M} - \alpha(trace\boldsymbol{M})^2\]

式中，\(det\boldsymbol{M}\)为矩阵\(\boldsymbol{M}=\begin{bmatrix}A&B\\B&C\end{bmatrix}\)的行列式；\(trace\boldsymbol{M}\)为矩阵M的直迹；\(\alpha\)为经验常数，取值范围为0.04~0.06。事实上，特征是隐含在\(det\boldsymbol{M}\)和\(trace\boldsymbol{M}\)中，因为，

\[det\boldsymbol{M} = \lambda_1\lambda_2=AC-B^2\] \[trace\boldsymbol{M}=\lambda_2+\lambda_2=A+C\]

Harris角点的性质

增大\(\alpha\)的值，将减小角点响应值R，降低角点检测的灵性，减少被检测角点的数量；减小\(\alpha\)值，将增大角点响应值R，增加角点检测的灵敏性，增加被检测角点的数量。

Harris角点检测算子对亮度和对比度的变化不敏感。这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置。

Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值R也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

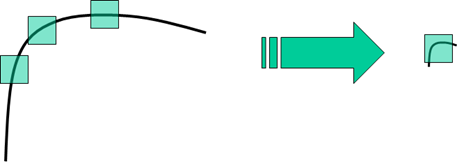
Harris角点检测算子不具有尺度不变性。如下图所示，当右图被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点。

为了解决尺度不变性问题，可以使用多尺度Harris角点算法，将Harris角点检测算子与高斯尺度空间表示相结合，使其具有尺度不变性：

\[\boldsymbol{M}=\mu(x,\sigma_I,\sigma_D)=\sigma_D^2g(\sigma_I)\otimes\begin{bmatrix}L_x^2(x,\sigma_D)&L_xL_y(x,\sigma_D)\\L_xL_y(x,\sigma_D)&L_y^2(x,\sigma_D)\end{bmatrix}\]

参考

http://blog.csdn.net/lwzkiller/article/details/54633670

Harris角点检测原理详解

http://www.cnblogs.com/ronny/p/4009425.html

Harris角点

https://blog.csdn.net/davebobo/article/details/52598850

检测并匹配兴趣点

https://blog.csdn.net/songzitea/article/details/17969375

角点匹配方法

https://mp.weixin.qq.com/s/LeFT029sd7-kRw1QTFUKmA

特征检测之Harris角点检测

Optical flow

基本概念

从本质上说，光流就是你在这个运动着的世界里感觉到的明显的视觉运动。例如，当你坐在火车上，然后往窗外看。你可以看到树、地面、建筑等等，他们都在往后退。这个运动就是光流。

一些比较远的目标，例如云、山，它们移动很慢，感觉就像静止一样。但一些离得比较近的物体，例如建筑和树，就比较快的往后退，然后离我们的距离越近，它们往后退的速度越快。可以通过不同目标的光流运动速度判断它们与我们的距离。

光流除了提供远近外，还可以提供角度信息。与咱们的眼睛正对着的方向成90度方向运动的物体速度要比其他角度的快。

以上是光流的一个直观的定义和特性，下面谈一下它的严谨的研究性定义。

光流的概念是Gibson在1950年首先提出来的。它是空间运动物体在观察成像平面上的像素运动的瞬时速度，是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系，从而计算出相邻帧之间物体的运动信息的一种方法。一般而言，光流是由于场景中前景目标本身的移动、相机的运动，或者两者的共同运动所产生的。

当人的眼睛观察运动物体时，物体的景象在人眼的视网膜上形成一系列连续变化的图像，这一系列连续变化的信息不断“流过”视网膜（即图像平面），好像一种光的“流”，故称之为光流（optical flow）。光流表达了图像的变化，由于它包含了目标运动的信息，因此可被观察者用来确定目标的运动情况。

研究光流场的目的就是为了从图片序列中近似得到不能直接得到的运动场。运动场（motion field），其实就是物体在三维真实世界中的运动；光流场，是运动场在二维图像平面上（人的眼睛或者摄像头）的投影。

光流约束方程

1981年，Horn和Schunck创造性地将二维速度场与灰度相联系，引入光流约束方程，得到光流计算的基本算法。人们基于不同的理论基础提出各种光流计算方法，算法性能各有不同。Barron等人对多种光流计算技术进行了总结，按照理论基础与数学方法的区别把它们分成四种：基于梯度的方法、基于匹配的方法、基于能量的方法、基于相位的方法。近年来神经动力学方法也颇受学者重视。

这里以最常见的亮度恒定（brightness consistancy）假设，介绍一下该假设下的光流约束方程的推导方法。

令\(I(x,y,t)\)表示t时刻的像素点\((x,y))\)的灰度值，则根据亮度恒定假设，我们有：

\[I(x,y,t) = I(x + \Delta x, y + \Delta y, t + \Delta t)\]

亮度恒定假设在现实中当然并不一定成立，但却是比较合理和自然的。只要\(\Delta t\)足够小，就基本能满足该假设。

我们对上式右侧进行一阶Taylor展开，可得：

\[I(x + \Delta x, y + \Delta y, t + \Delta t) \approx I(x,y,t) + \frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t\]

根据亮度恒定假设可得：

\[\frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t = 0\]

上式即为亮度恒定假设的光流约束方程。由于这个方程有两个未知数，所以没有唯一解。为了得到唯一解，就必须新增约束或假设，因此也就有了如下不同的算法。

名称	约束或假设
Lukas-Kanade	亮度恒定假设+局部光流恒定
Farneback	梯度恒定假设+局部光流恒定
Horn-Schunck	亮度恒定假设+光流场平滑
Brox	亮度恒定假设+梯度恒定假设+光流场平滑

参考

http://blog.csdn.net/zouxy09/article/details/8683859

光流Optical Flow介绍与OpenCV实现

http://www.cnblogs.com/walccott/p/4956858.html

Horn-Schunck光流法

http://blog.csdn.net/u014568921/article/details/46638557

目标跟踪之Lukas-Kanade光流法

http://www.cnblogs.com/gnuhpc/archive/2012/12/04/2802124.html

Lucas–Kanade光流算法

http://www.cnblogs.com/dzyBK/p/5096860.html

光流算法：Brox算法

http://www.cnblogs.com/quarryman/p/optical_flow.html

图像分析之光流之经典

https://zhuanlan.zhihu.com/p/31726032

走进光流的世界

https://mp.weixin.qq.com/s/nW6ZmEiio3VgX_LEktkxUA

视频目标检测：Flow-based

https://mp.weixin.qq.com/s?__biz=MzA4MDExMDEyMw==&mid=2247487121&idx=1&sn=c9ac1802ff79eb3ed86041dfe8781558

OpenCV4中DIS光流算法与应用

TLD

http://blog.csdn.net/zouxy09/article/details/7893011

TLD（Tracking-Learning-Detection）学习与源码理解系列文章

http://blog.csdn.net/carson2005/article/details/7647500

比微软kinect更强的视频跟踪算法–TLD跟踪算法介绍

http://www.cnblogs.com/lxy2017/p/3927456.html

TLD（Tracking-Learning-Detection）一种目标跟踪算法

ORB

ORB（Oriented FAST and Rotated BRIEF）特征，从它的名字中可以看出它是对FAST特征点与BREIF特征描述子的一种结合与改进，这个算法是由Ethan Rublee,Vincent Rabaud,Kurt Konolige以及Gary R.Bradski在2011年一篇名为“ORB：An Efficient Alternative to SIFT or SURF”的文章中提出。

参考：

http://www.cnblogs.com/ronny/p/4083537.html

ORB特征点检测

https://zhuanlan.zhihu.com/p/52140541

传统计算机视觉中图像特征匹配方法的原理介绍（SIFT和ORB）

背景提取

背景提取是在视频图像序列中提取出背景，背景就是场景中静止不动的景物。因为摄像机不动，因此图像中的每个像素点都有一个对应的背景值，在一段时间内，这个背景值是比较固定的。背景提取的目标就是根据视频图像序列，找出图像中每一点的背景值。

参考：

https://blog.csdn.net/ajianyingxiaoqinghan/article/details/72628402

背景提取算法——帧间差分法、背景差分法、ViBe算法、ViBe+算法

https://blog.csdn.net/tiandijun/article/details/50499708

ViBe算法原理和代码解析

http://www.cnblogs.com/dwdxdy/p/3527891.html

背景建模——VIBE

https://www.cnblogs.com/ywsoftware/p/4434074.html

运动目标检测ViBe算法