• 霍夫变换（续）
• Eigenface
  • 计算Eigenface
  • 使用Eigenface
  • Eigenface的缺点
  • 参考
• LBP
  • LBP特征提取
  • 圆形LBP算子
  • LBP等价模式
  • LBP特征匹配
  • Histogram intersection
  • Chi square statistic

霍夫变换（续）

参考：

http://www.cs.jhu.edu/~misha/Fall04/GHT1.pdf

Hough Transform

http://blog.csdn.net/poem_qianmo/article/details/26977557

OpenCV霍夫变换：霍夫线变换，霍夫圆变换合辑

http://blog.csdn.net/tianwaifeimao/article/details/17678669

基于LSD的直线提取算法

https://mp.weixin.qq.com/s/WV78mvRn-cYm11cL4l2ScA

开源、快速、高精度的椭圆检测—你值得拥有！

https://mp.weixin.qq.com/s/QEX46FBulPeGEwdlp469hg

基于霍夫变换进行线检测

https://mp.weixin.qq.com/s/pG-7p74-VGT9JpN-cS3i_Q

南开大学提出深度霍夫变换：语义线检测新方法

Eigenface

Eigenface是M. Turk和A. Pentland于1991年提出的人脸识别算法。

Matthew A. Turk，Virginia Tech本科（1982）+CMU硕士（1984）+MIT博士（1991）。UCSB教授。

Alex Paul “Sandy” Pentland，1952年生，MIT博士（1982）。MIT教授。

论文：

《Face recognition using eigenfaces》

计算Eigenface

Step 1：假设有M张训练照片\(I_1,\dots,I_M\)，每张照片的尺寸为NxN，将照片\(I_i\)转换成1维vector \(\Gamma_i\)。显然，\(\Gamma_i\)的大小是\(N^2\)。

Step 2：计算均值vector \(\Psi\)（也就是常说的平均脸（average face/mean face））：

\[\Psi=\frac{1}{M}\sum_{i=1}^M\Gamma_i\]

Step 3：计算图片与均值的差：

\[\Phi_i=\Gamma_i-\Psi\]

Step 4：计算协方差矩阵：

\[C=\frac{1}{M}\sum_{n=1}^M\Phi_n \Phi_n^T=AA^T(N^2\times N^2 \text{matrix})\]

Step 5：计算的\(AA^T\)特征向量\(u_i\)。然而，\(AA^T\)太大了，我们只能退而求其次计算\(A^TA(M\times M \text{matrix})\)的特征向量\(v_i\)。

那么\(u_i\)和\(v_i\)到底有什么关系呢？我们首先根据特征向量的定义，给出下式：

\[A^TAv_i=\mu_iv_i\]

其中，\(\mu_i\)是\(A^TA\)的特征值。

\[A^TAv_i=\mu_iv_i\Rightarrow AA^TAv_i=\mu_iAv_i\Rightarrow CAv_i=\mu_iAv_i\]

令\(u_i=Av_i\)，则：

\[Cu_i=\mu_iu_i\]

可见\(\mu_i\)同时也是\(AA^T\)的特征值，而对应的特征向量则是\(Av_i\)。

实际上，\(A^TA\)的M个特征值，就是\(AA^T\)的前M大的特征值。

Step 6：从中选出K个最大的特征向量供后续使用。

使用Eigenface

Step 1：给定图片\(\Gamma\)，计算：

\[\Phi=\Gamma-\Psi\]

Step 2：将\(\Phi\)映射到K维特征向量空间：

\[\Omega=[w_1,\dots,w_K]^T\]

Step 3：计算与图片l的距离：

\[e_r=\|\Omega-\Omega^l\|\]

当\(e_r<T_r\)时，就认为是同一张人脸。

这里的距离可以是欧氏距离，但作者指出使用马式距离效果更佳。

综上，Eigenface实际上就是PCA在人脸识别上的应用。

Eigenface的缺点

1.训练图片中人脸需要对齐，且图片大小一致。

2.Eigenface对于大数据集的计算效率不佳。在Eigenface出现的年代，数字图片尚不多见，因此，数据集普遍较小。但现在即便是mini数据集也动辄上万张图片，甚至\(M>N^2\)的情况也不罕见。而对超大矩阵进行SVD分解，是个很吃计算量的事情，这也限制了Eigenface的应用。

参考

http://blog.csdn.net/smartempire/article/details/21406005

特征脸方法（Eigenface）

http://vision.jhu.edu/teaching/vision08/Handouts/case_study_pca1.pdf

Eigenfaces for Face Detection/Recognition

http://www.cnblogs.com/little-monkey/p/8118938.html

人脸识别算法——EigenFace、FisherFace、LBPH

LBP

LBP（Local Binary Patterns）算法是Matti Kalevi Pietikäinen于1994年提出的方法，后来被用到了人脸识别领域。

Matti Kalevi Pietikäinen，University of Oulu博士（1982）、教授。

Timo Ojala，Pietikäinen的博士生。现亦为University of Oulu教授。

论文：

《Face Recognition with Local Binary Patterns》

LBP特征提取

最初的LBP是定义在像素3x3邻域内的，以邻域中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3x3邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该邻域中心像素点的LBP值，并用这个值来反映该区域的纹理信息。如下图所示：

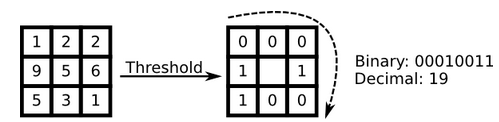
即：

\[LBP(x_c,y_c)=\sum_{p=0}^{P-1}2^ps(i_p-i_c)\]

其中，c表示中心元素，p表示领域内的其它元素。

\[s(x)=\begin{cases} 1, & \text{if } x \ge 0 \\ 0, & \text{else} \\ \end{cases}\]

圆形LBP算子

基本的LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala等对LBP算子进行了改进，将3x3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的LBP算子允许在半径为R的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子。比如下图定了一个5x5的邻域：

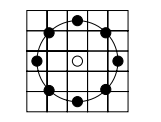
上图内有八个黑色的采样点，每个采样点的值可以通过下式计算：

\[x_p=x_c+R\cos(\frac{2\pi p}{P})\\ y_p=y_c-R\sin(\frac{2\pi p}{P})\]

通过上式可以计算任意个采样点的坐标，但是计算得到的坐标未必完全是整数，所以可以通过双线性插值来得到该采样点的像素值：

\[f(x,y)\approx \begin{bmatrix} 1-x & x \\ \end{bmatrix} \begin{bmatrix} f(0,0) & f(0,1) \\ f(1,0) & f(1,1) \\ \end{bmatrix} \begin{bmatrix} 1-y \\ y \\ \end{bmatrix}\]

LBP等价模式

一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生\(2^p\)种模式。很显然，随着邻域集内采样点数的增加，二进制模式的种类是急剧增加的。例如：5×5邻域内20个采样点，有\(2^{20}\)＝1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。

同时，过多的模式种类对于纹理的表达是不利的。例如，将LBP算子用于纹理分类或人脸识别时，常采用LBP模式的统计直方图来表达图像的信息，而较多的模式种类将使得数据量过大，且直方图过于稀疏。因此，需要对原始的LBP模式进行降维，使得数据量减少的情况下能最好的代表图像的信息。

为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”（Uniform Pattern）来对LBP算子的模式种类进行降维。Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类。

通过这样的改进，二进制模式的种类大大减少，而不会丢失任何信息。模式数量由原来的\(2^p\)种减少为\(p(p-1)+2\)种。这种丢掉2次以上跳变信息的方法，实际上就是一种高频滤波。

LBP特征匹配

如果将以上得到的LBP值直接用于人脸识别，其实和不提取LBP特征没什么区别，会造成计算量准确率等一系列问题。我们可以将一副人脸图像分为7x7的子区域，并在子区域内根据LBP值统计其直方图，以直方图作为其判别特征。这样做的好处是在一定范围内避免图像没完全对准的情况，同时也对LBP特征做了降维处理。

对于得到的直方图特征，有多种方法可以判别其相似性。常见的有Histogram intersection和Chi square statistic。

Histogram intersection

Histogram intersection出自以下论文：

《The Pyramid Match Kernel: Discriminative Classification with Sets of Image Features》

Kristen Grauman，Boston College本科（2001）+MIT硕士（2003）+MIT博士（2006），University of Texas at Austin教授，Marr Prize（2011）。导师是Trevor Darrell。
绝对的美女，靠脸吃饭都没问题的那种。
个人主页：
http://www.cs.utexas.edu/~grauman/
从她的主页来看，她手下有很多亚裔学生。还有一些在线课程，其中有部分是博士课程，只适合高手挑战。

David Courtnay Marr，1945～1980，英国神经学家和生理学家。Trinity College, Cambridge博士（1972），MIT教授。35岁死于白血病。他在神经科学，尤其是视觉方面有重大贡献。
Marr Prize由International Conference on Computer Vision颁发，2年一次，是CV界的最高荣誉。何恺明是去年（2017）的新晋得主。

假设图像或其他数据的特征可以构成直方图，根据直方图间距的不同可以得到多种类型的直方图：

\[\Psi(x)=[H_{-1}(x),H_0(x),\dots,H_L(x)]\]

H的下标每增加1,则直方图间距变为原来的两倍。\(H_{-1}\)表示每个样本都有自己的bin，而\(H_L\)表示所有的样本都在一个bin中。

两个数据集的相似度可以用下式来匹配：

\[K_\Delta(\Psi(y),\Psi(z))=\sum_{i=0}^Lw_iN_i\]

其中，\(w_i=\frac{1}{2^i},N_i=I(H_i(y),H_i(z))-I(H_{i-1}(y),H_{i-1}(z))\)。

I的计算方法如下图所示：

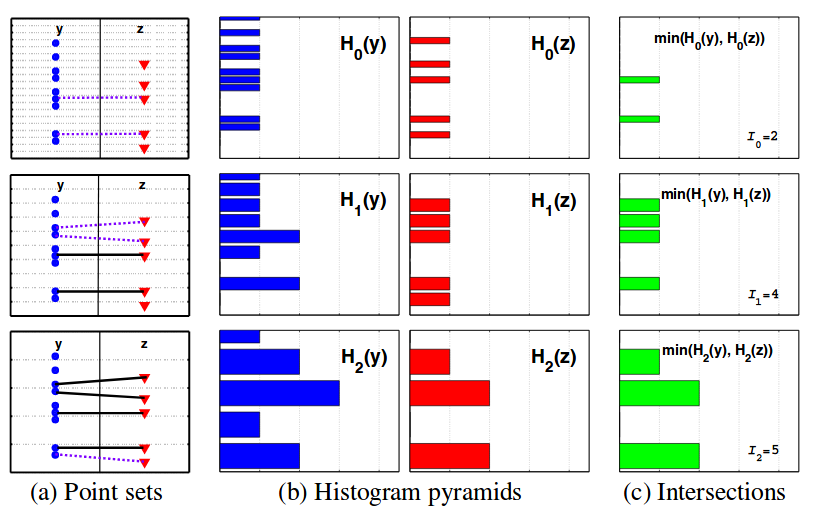
(a)里的y和z代表两种数据分布，三幅图代表三层金字塔，每一层里有间距相等的虚线。

可以看到红点蓝点的位置是固定的，但是根据直方图宽度的不同可以划到不同的直方图里，如(b)所示。

(c)图就是L的计算结果，是通过(b)里两种直方图取交集得来的。

注意：这里的I表示的是交集里元素的个数（即(a)中的连线数），而不是交集的个数（即(c)中的绿条个数）。

Chi square statistic

在《数学狂想曲（五）》中，我们给出了\(\chi^2\)检验的原理和公式。这里仅对于直方图相似度给出最后的公式：

\[\chi_w^2(S,M)=\sum_{i,j}w_j\frac{(S_{i,j}-M_{i,j})^2}{S_{i,j}+M_{i,j}}\]

其中，i为图像的某块小区域，j为小区域内直方图的某一列的值。\(w_j\)是每块小区域的权重，比如在人脸区域中，眼睛、嘴巴等区域包含的信息量更为丰富，那么这些区域的权重就可以设置的大一些。