• Meanshift
  • Meanshift聚类（续）
  • 反向投影图
  • Meanshift与目标跟踪
  • Meanshift与图像分割
• Camshift
• Harris
  • 角点
  • Harris Corner Detector

Meanshift

Meanshift聚类（续）

基本的Mean Shift形式存在一个问题：在\(S_h\)的区域内，每一个点对x的贡献是一样的。而实际上，这种贡献与x到每一个点之间的距离是相关的。同时，对于每一个样本，其重要程度也是不一样的。

到了1995年，Yizong Cheng（现为University of Cincinnati副教授）对基本的Mean Shift算法在以下两个方面做了推广。

首先，定义了一族核函数,使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同。

其次，还设定了一个权重系数,使得不同的样本点重要性不一样,这大大扩大了Mean Shift的适用范围。

基于以上的考虑，可对基本的Mean Shift向量形式中增加核函数和样本权重，得到如下的改进的Mean Shift向量形式：

\[M_h\left ( x \right )=\frac{\sum_{i=1}^{n}G_H\left ( x_i-x \right )w\left ( x_i \right )\left ( x_i-x \right )}{\sum_{i=1}^{n}G_H\left ( x_i-x \right )w\left ( x_i \right )}\]

其中：

\[G_H\left ( x_i-x \right )=\left | H \right |^{-\frac{1}{2}}G\left ( H^{-\frac{1}{2}}\left ( x_i-x \right ) \right )\]

G(x)是一个单位的核函数。H是一个正定的对称d×d矩阵，称为带宽矩阵，其是一个对角阵。\(w\left ( x_i \right )\geqslant 0\)是每一个样本的权重。对角阵H的形式为：

\[H=\begin{bmatrix} h_1^2 & 0 & \cdots & 0\\ 0 & h_2^2 & \cdots & 0\\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & h_d^2 \end{bmatrix}_{d\times d}\]

因此，上述Mean Shift向量也可以改写成：

\[M_h\left ( x \right )=\frac{\sum_{i=1}^{n}G\left ( \frac{x_i-x}{h_i} \right )w\left ( x_i \right )\left ( x_i-x \right )}{\sum_{i=1}^{n}G\left ( \frac{x_i-x}{h_i} \right )w\left ( x_i \right )}\]

这里的核函数可以是Uniform核，也可以是Gaussian核。

参考：

https://wenku.baidu.com/view/5862334827d3240c8447ef40.html

meanshift算法简介

http://www.cnblogs.com/liqizhou/archive/2012/05/12/2497220.html

Meanshift，聚类算法

https://wenku.baidu.com/view/0d9eb876a417866fb84a8eb2.html

mean-shift算法概述

http://www.cnblogs.com/cfantaisie/archive/2011/06/10/2077188.html

meanshift聚类

https://blog.csdn.net/google19890102/article/details/51030884

Mean Shift聚类算法

反向投影图

在继续介绍Meanshift之前，我们先引入反向投影图的概念。

首先，我们对图像的像素值按照某种特征进行直方图统计，得到一组bin值。

然后，计算位置x上的bin值，并用该bin值替换原来的像素值，就得到了反向投影图。

参考：

https://blog.csdn.net/poiiy333/article/details/9051409

反向投影图

http://www.cnblogs.com/zsb517/archive/2012/06/20/2556508.html

opencv直方图反向投影

Meanshift与目标跟踪

由于RGB对光照的变化比较敏感，而这种敏感对目标跟踪而言是不利的。因此，通常我们要将图像转换到HSV颜色空间。

首先，统计目标box区域内H（色调）分量的直方图，并对其进行归一化，使得该直方图成为概率直方图。这一步相当于统计目标的颜色特征。

然后，使用统计得到的概率直方图，将全图转换为反向投影图，并应用Meanshift算法。由于前后两帧中目标通常不会隔的太远，原目标中心可能仍在目标范围内。因此，目标中心会向反向投影图中概率大的地方移动，从而达到了目标跟踪的效果。

总结：用meanshift进行跟踪最重要的一点是输入图像的把握，也就是要让它的迭代能越来越迭代到目标上。这种图像也不一定就是反向投影图，只要是一幅反映当前图像中每个像素点含有目标概率的图就可以了。反向投影图恰好就是这样的一幅图而已。

优点：

（1）算法计算量不大，在目标区域已知的情况下完全可以做到实时跟踪；

（2）采用核函数直方图模型，对边缘遮挡、目标旋转、变形和背景运动不敏感。

缺点：

（1）缺乏必要的模板更新；

（2）跟踪过程中由于窗口宽度大小保持不变，当目标尺度有所变化时，跟踪就会失败；

（3）当目标速度较快时，跟踪效果不好；

（4）直方图特征在目标颜色特征描述方面略显匮乏，缺少空间信息；

参考：

https://blog.csdn.net/li_dongxuan/article/details/70667170

目标跟踪：Meanshift, Camshift

http://www.cnblogs.com/cfantaisie/archive/2011/06/10/2077190.html

meanshift目标跟踪算法总结

https://blog.csdn.net/jinshengtao/article/details/30258833

基于MeanShift的目标跟踪算法及实现

https://mp.weixin.qq.com/s/Wa64-PjRAgZU_j5EmRQiPg

OpenCV中MeanShift算法视频移动对象分析

Meanshift与图像分割

除此之外，mean shift还可以用于图像分割。

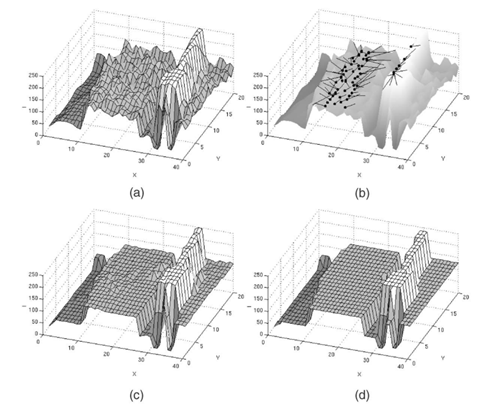
如上图所示，算法过程可分三步走：模点搜索/图像平滑、模点聚类/合并相似区域、兼并小区域（可选）。

模点搜索是为了找到每个数据点的到类中心，以中心的颜色代替自己的颜色，从而平滑图像。

但模点搜索得到的模点太多，并且很多模点挨得很近，若果将每个模点都作为一类的话，类别太多，容易产生过分割，即分割太细，所以要合并掉一些模点，也就是合并相似区域。

模点聚类后所得到的分割区域中，有些区域所包含的像素点太少，这些小区域也不是我们想要的，需要再次合并。

参考：

https://blog.csdn.net/ttransposition/article/details/38514127

mean shift图像分割

Camshift

Camshift算法是Continuously Adaptive Mean Shift algorithm的简称。它是一个基于MeanSift的改进算法。它首次由Gary R.Bradski等人提出和应用在人脸的跟踪上，并取得了不错的效果。

由于Meanshift在跟踪中搜索框的大小一直不变，对目标的尺度变化不具有鲁棒性。Camshift针对此点设计了自适应算法用于调整窗口的大小。该方法共有两步：

扩大：在计算窗口大小前，在MeanShift算出的窗口的四个方向上增大了TOLERANCE，即高和宽都增大了2TOLERANCE（此值自己调整设置）。

缩小：在扩大的窗口内重新计算0阶矩，1阶矩和2阶矩，利用矩的值重新计算高和宽。

缺点：

（1）只利用颜色统计做的跟踪，在背景有相似颜色时，会出现跟踪错误的情况。

（2）不能做多目标跟踪。

（3）由于它只在初始位置（而不是从每个像素点）开始迭代，所以有可能在初始位置错了后，收敛的位置还是原位置（即跟丢了后，可能会找不回来）。

参考：

http://blog.sina.com.cn/s/blog_5d1476580101a57j.html

Camshift算法

https://wenku.baidu.com/view/59596ac42cc58bd63186bd37.html

Camshift算法原理

https://zhuanlan.zhihu.com/p/26970589

基于Camshift算法的小球跟踪

Harris

角点

角点是图像很重要的特征,对图像图形的理解和分析有很重要的作用。角点在保留图像图形重要特征的同时,可以有效地减少信息的数据量,使其信息的含量很高,有效地提高了计算的速度,有利于图像的可靠匹配,使得实时处理成为可能。角点在三维场景重建运动估计，目标跟踪、目标识别、图像配准与匹配等计算机视觉领域起着非常重要的作用。

下面有两幅不同视角的图像，通过找出对应的角点进行匹配。

我们可以直观的概括下角点所具有的特征：

轮廓之间的交点；

对于同一场景，即使视角发生变化，通常具备稳定性质的特征；

该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化；

角点匹配（corner matching）是指寻找两幅图像之间的特征像素点的对应关系，从而确定两幅图像的位置关系。

角点匹配可以分为以下四个步骤：

提取检测子：在两张待匹配的图像中寻找那些最容易识别的像素点(角点)，比如纹理丰富的物体边缘点等。

提取描述子：对于检测出的角点，用一些数学上的特征对其进行描述，如梯度直方图，局部随机二值特征等。检测子和描述子的常用提取方法有:sift, harris, surf, fast, agast, brisk, freak, brisk,orb等。

匹配：通过各个角点的描述子来判断它们在两张图像中的对应关系。常用方法如flann。

去外点：去除错误匹配的外点，保留正确的内点。常用方法有Ransac, GTM。

这里我们只介绍最常用的Harris算子。

Harris Corner Detector

Harris Corner Detector是Chris Harris和Mike Stephens于1988年提出的算子。

论文：

《A Combined Corner and Edge Detector》

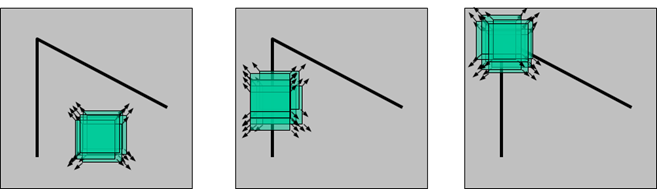
如上图所示。人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果在各个方向上移动这个特征的小窗口，窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了角点。如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在角点；如果窗口在某一个方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，那么，窗口内的图像可能就是一条直线的线段。

对于图像\(I(x,y)\)，当在点(x,y)处平移\((\Delta x,\Delta y)\)后的自相似性，可以通过自相关函数给出：

\[c(x,y;\Delta x,\Delta y) = \sum_{(u,v)\in W(x,y)}w(u,v)(I(u,v) – I(u+\Delta x,v+\Delta y))^2\]

其中，\(W(x,y)\)是以点(x,y)为中心的窗口，\(w(u,v)\)为加权函数，它既可是常数，也可以是高斯加权函数。

根据泰勒展开，对图像\(I(x,y)\)在平移\((\Delta x,\Delta y)\)后进行一阶近似：

\[I(u+\Delta x,v+\Delta y) = I(u,v)+I_x(u,v)\Delta x+I_y(u,v)\Delta y+O(\Delta x^2,\Delta y^2)\approx I(u,v)+I_x(u,v)\Delta x+I_y(u,v)\Delta y\]

其中，\(I_x,I_y\)是图像\(I(x,y)\)的偏导数，则自相关函数可简化为：

\[c(x,y;\Delta x,\Delta y)\approx \sum_w (I_x(u,v)\Delta x+I_y(u,v)\Delta y)^2=[\Delta x,\Delta y]M(x,y)\begin{bmatrix}\Delta x \\ \Delta y\end{bmatrix}\]