graphics » 图像处理理论(一)——概述, 直方图, 二值化
2016-04-30 :: 4996 Words书籍
《Digital Image Processing》,Rafael C. Gonzalez、Richard E. Woods著。
Rafael C. Gonzalez,佛罗里达大学博士,田纳西大学教授。
Richard E. Woods,田纳西大学博士和教授。
《Image Processing, Analysis and Machine Vision》,Milan Sonka、Vaclav Hlavac、Roger Boyle著。
Milan Sonka,艾奥瓦大学教授。
Vaclav Hlavac,捷克科技大学博士和教授。
Roger Boyle,利兹大学教授。
《Computer Vision: Principles, Algorithms, Applications, Learning》
Roy Davies,英国伦敦大学皇家霍洛威学院机器视觉荣誉教授。
近年来,由于深度学习的崛起,传统CV算法基本都已经过时了。这个blog系列主要对传统算法进行有针对性的讲述,也包括一些传统CV和DL CV共有的概念的讲解。
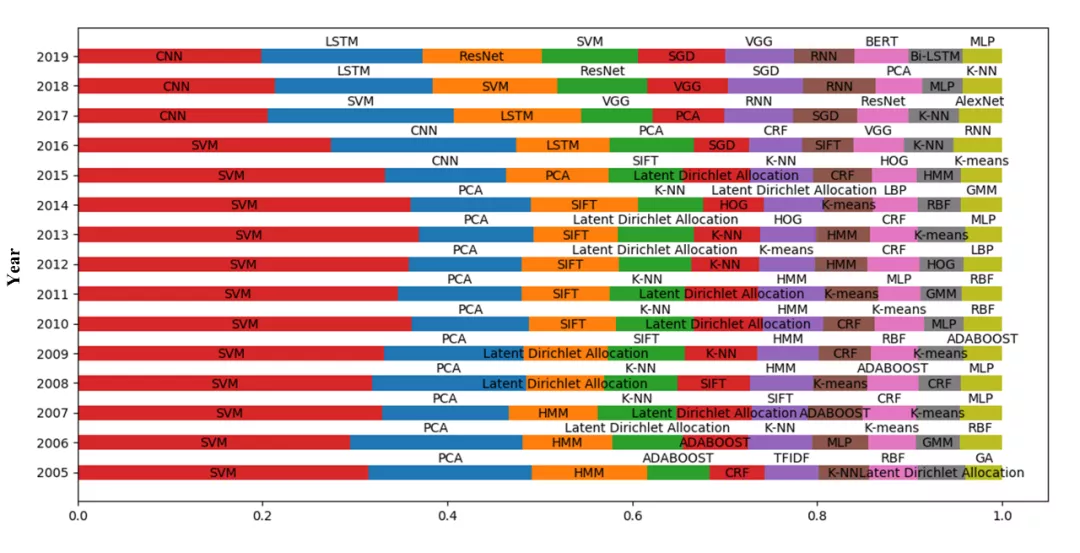
参考:
https://mp.weixin.qq.com/s/rOgI5Vmj5i43RI1iHdSVXg
866页《计算机视觉:原理,算法,应用,学习》最新第五版-附下载
https://mp.weixin.qq.com/s/8ensybSIt8nedFtNZctKpA
图像处理手册第七版,1032页pdf
历史
模拟图像
所谓模拟图像:就是通过某种物理量(如光、电等)的强弱变化来记录图像亮度信息。
模拟图像的出现应该从1826年前后法国科学家Joseph Nicéphore Niépce发明第一张可以永久记录的照片开始,到如今已将近两百年。
从19世纪30年代到20世纪中期计算机的出现,中间有一百多年的历史。那时候的图像的发展史,实际上差不多就是摄影的发展史。
数字图像
数字图像的诞生并不与计算机完全挂钩。
战争往往是催生技术发展的最好外部因素,在第一次世界大战后的两年,也就是1920年数字图像被发明了,用于报纸行业。
当时为了传输这一幅图像,巴特兰有线电视图像传输系统(Bartlane cable picture transmission system)被发明,实际上主体就是一根海底电缆,从英国伦敦连接到美国纽约。
1921年实现了第一幅数字图像的传送,耗时3小时,编码解码都是用打印机来完成的。
当时用了5个灰度级进行编码,因为人眼就只能分辨这么多,分的再细也没有用。
20世纪50年代电子计算机被发明,人们开始利用计算机来处理图像,数字图像处理则开始正式作为一门学科在20世纪60年代初期诞生。
早期的图像处理的目的是改善图像的质量,美国喷气推进实验室(JPL)对航天探测器徘徊者7号在1964年发回的几千张月球照片使用了图像处理技术,包括几何校正、灰度变换、去除噪声等方法进行处理,成功地绘制出月球表面地图,这可以算是最早的数字图像处理了。
参考
https://mp.weixin.qq.com/s/FjQfAYKCgZ1ToE4nVyr28A
图像与CNN发家简史,集齐深度学习三巨头
CV/CG

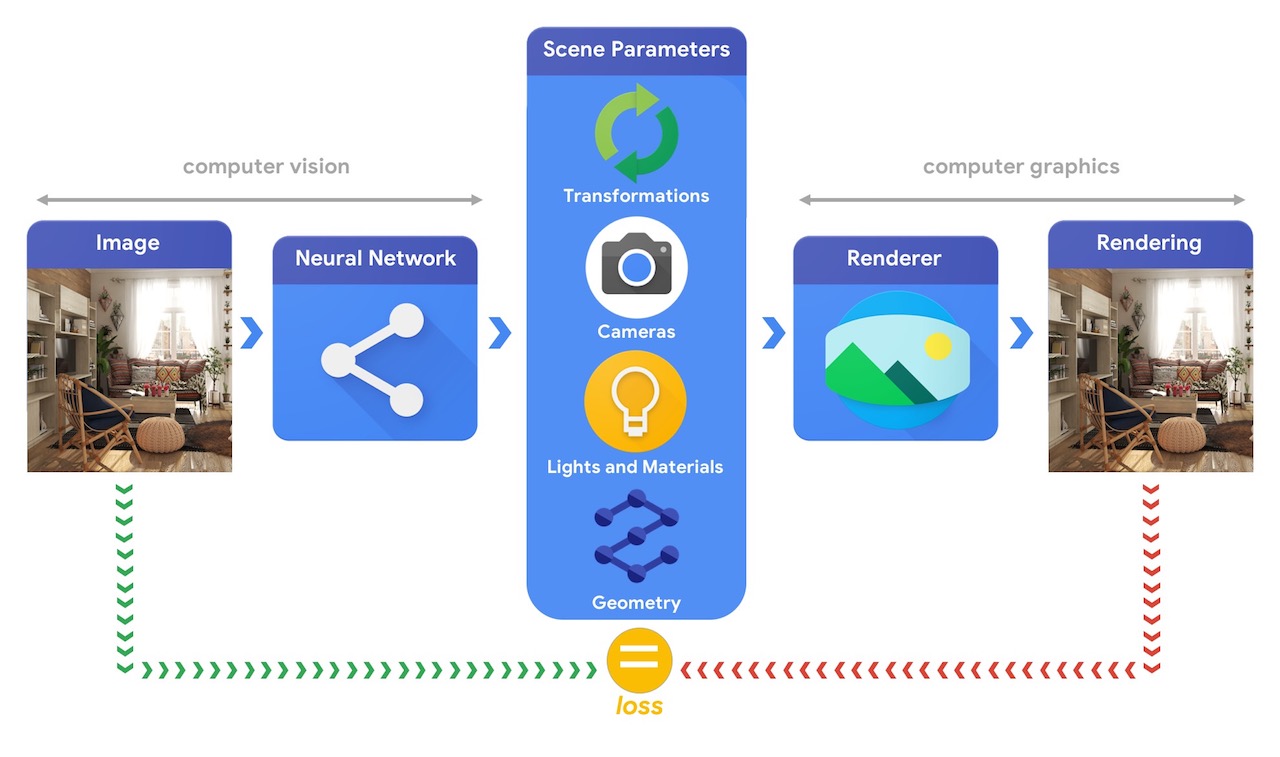
一般来说,CV和CG是两个相反的过程,但是也有交集的领域例如AR/VR。
特征工程
颜色特征:RGB、HSV、Lab
几何特征:Edge、Corner、Blob
纹理特征:HOG、LBP、Gabor
局部特征:SIFT、SURF、ORB、FAST
对比度和亮度
\[g(i,j)=a\times f(i,j)+b\]上式中\(f(i,j)\)和\(g(i,j)\)表示位于第i行,第j列的像素。上述线性变换中,a表示对比度,b表示亮度。
邻域
\[\left[ \begin{array}{ccc} A_0&A_1&A_2\\ A_3&A&A_4 \\ A_5&A_6&A_7\end{array} \right]\]\(A_0\)~\(A_7\)被称作像素A的1度8-邻域(即\(U(A,1)\)),相应的上下左右的四个像素\(A_1\)、\(A_3\)、\(A_4\)、\(A_6\)被称作像素A的1度4-邻域。下文如无特别指出,邻域均为8-邻域。
4-邻域也叫Von Neumann neighborhood,8-邻域也叫Moore neighborhood。
John von Neumann,1903~1957,匈牙利裔美国人,数学家,物理学家,计算机科学家。Pázmány Péter University博士,哥廷根大学博士后,导师David Hilbert,普林斯顿大学教授。参与曼哈顿计划,提出了von Neumann架构,也是量子计算领域的奠基人。没错,就是现在很火的那个量子计算。
Edward Forrest Moore,1925~2003,美国数学家,计算机科学家。Brown University博士,University of Wisconsin–Madison教授。
定义\(U^+(A,N)=A\bigcup\limits_{i=1}^N U(A,i)\)。
\(U(A,2)\)的定义如下:
如果\(B\in U(A,1)\land C\in U(B,1)\land C\notin U^+(A,1)\),那么\(C\in U(A,2)\)。
类似的\(U(A,N)\)的定义为:
如果\(B\in U(A,N-1)\land C\in U(B,1)\land C\notin U^+(A,N-1)\),那么\(C\in U(A,N)\)。
这里的N被称为度数,也就是两点间的距离,即\(L(A,C)=N\)。
相关算子
相关(Correlation)算子
\[g=f\otimes h\]的定义为:
\[g(i,j)=\sum_{k,l}f(i+k,j+l)h(k,l)\]其中,h称为相关核(Kernel),即滤波器的加权系数矩阵,有的书上也称作“模板”。相关核有个叫做锚点(anchor)的属性,也就是被滤波的那个点在核中的位置。以3*3的h矩阵为例,如果锚点在矩阵中央的话,则\(i-1\le k\le i+1,j-1\le l\le j+1\)。如果锚点在左上角的话,则\(i\le k\le i+2,j\le l\le j+2\)。
所有的点\((k,l)\)组成的集合,叫做核空间。一般也简单记作\(X_{k,l}\)。这里的X可以是累加、求均值、求最大值、求最小值等集合运算符。
此外,h矩阵还有是否归一化的属性。这里将计算矩阵中所有元素之和的操作,记作\(SUM(h)\).则当\(SUM(h)=1\)时,h为归一化核。\(\frac{h}{SUM(h)}\),称作核的归一化。
卷积算子
卷积(Convolution)算子
\[g=f\ast h\]的定义为:
\[g(i,j)=\sum_{k,l}f(i-k,j-l)h(k,l)\]显然
\[f\ast h=f\otimes rot180(h)\]其中,rotN表示将矩阵元素绕中心逆时针旋转N度,显然这里的N只有为90的倍数,才是有意义的。
灰度化
以RGB格式的彩图为例,通常灰度化采用的方法主要有:
方法1:\(Gray=(R+G+B)/3\)
方法2:\(Gray=max(R,G,B)\)
方法3:\(Gray=0.299R+0.587G+0.114B\)(这种参数考虑到了人眼的生理特点)
灰度直方图
灰度直方图是灰度级的函数,描述图像中该灰度级的像素个数(或该灰度级像素出现的频率):其横坐标是灰度级,纵坐标表示图像中该灰度级出现的个数(频率)。
一维直方图的结构表示为:
\[N(P)=[n_1,n_2,\dots,n_{L-1}]\] \[N=\sum_{i=0}^{L-1}n_i,p_i=\frac{n_i}{N}\]其中,L为灰度级的个数,\(n_i\)为每个灰度的像素个数,其出现概率为\(p_i\)。
同理,可将灰度直方图的概念推广到单独的颜色通道,即所谓的颜色直方图。如下图所示:
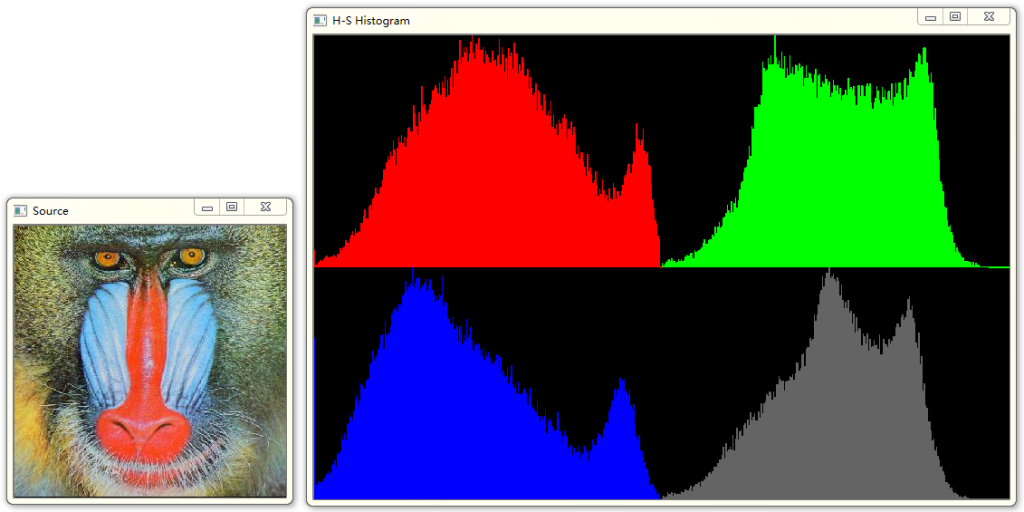
直方图均衡化
直方图均衡化是通过灰度变换将一幅图像转换为另一幅具有均衡直方图,即在每个灰度级上都具有尽可能相同的象素点数(即均匀分布)的过程。
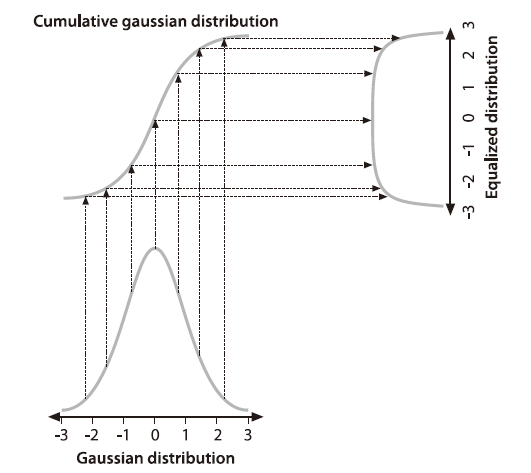
上图展示的是,将一个高斯分布的直方图转换为均匀分布的直方图的过程,其中累积分布函数起到了桥梁作用。事实上,任意分布的函数都可以通过这样的方式转换为另一种分布函数。而直方图均衡化,就是将其他分布函数的直方图转换成均匀分布的直方图的过程。
具体计算方法如下:
1.建立图像灰度直方图。
2.计算累积分布函数\(P(k)\)。
\[P(k)=\sum_{i=0}^{k}p_i\]3.生成新的灰度和旧的灰度的对应关系数组。
\[T(i)=P(i)*L\]其中\(T(i)\)表示对应原来的灰度i的新灰度值。
4.用新的灰度值替换旧的灰度值。
直方图均衡化的效果如下所示:

原图

效果图
直方图均衡化主要处理那些曝光不够或者曝光过度的图片,可以显著提高这些图片的对比度。但其本质是扩大了量化间隔,而量化级别反而减少了,因此,原来灰度不同的象素经处理后可能变的相同,形成了一片的相同灰度的区域,各区域之间有明显的边界,从而出现了伪轮廓。这种效应也称作“灰度吞噬效应”。
彩色直方图的均衡化有以下几种方法:
1.统计所有RGB颜色通道的直方图的数据并做均衡化运算,然后根据均衡化所得的映射表分别替换R、G、B通道颜色值。
2.分别统计R、G、B颜色通道的直方图的数据并做均衡化运算,然后根据R、G、B的映射表分别替换R、G、B通道颜色值。
3.用亮度公式或求RGB的平均值的方式计算亮度通道,然后统计亮度通道的直方图的数据并做均衡化运算,然后根据映射表分别替换R、G、B通道颜色值。
参考:
https://zhuanlan.zhihu.com/p/44918476
直方图均衡化
https://mp.weixin.qq.com/s/30YMHQNGYaY3K5SCBHCG2g
没想到图像直方图有这么多应用场景
二值化
二值图也就是黑白图。将灰度图转换成黑白图的过程,就是二值化。二值化的一般算法是:
\[g=\begin{cases} 0, & f\le t \\ 1, & f>t \\ \end{cases}\]其中\(t\)被称为阀值。阀值的确定方法有下面几种。
Otsu法(大津法或最大类间方差法)
该算法是一种动态阈值分割算法。它的主要思想是按照灰度特性将图像划分为背景和目标2部分(这里我们将\(f\le t\)的部分称为背景,其他部分称为目标。),选取门限值,使得背景和目标之间的方差最大。
Nobuyuki Otsu(大津展之),东京大学博士,先后在筑波大学和东京大学担任教授。
其步骤如下:
1.建立图像灰度直方图。
2.计算背景和目标的出现概率。
\[p_A=\sum_{i=0}^{t}p_i,p_B=\sum_{i=t+1}^{L-1}p_i=1-p_A\]其中,A和B分别表示背景部分和目标部分。
3.计算A和B两个区域的类间方差。
\[\omega_A=\frac{\sum_{i=0}^{t}ip_i}{p_A},\omega _B=\frac{\sum_{i=t+1}^{L-1}ip_i}{p_B}(公式1)\]公式1分别计算A和B区域的平均灰度值;
\[\omega_0=p_A\omega_A+p_B\omega_B=\sum_{i=0}^{L-1}ip_i(公式2)\]公式2计算灰度图像全局的灰度平均值;
\[\sigma^2=p_A(\omega_A-\omega_0)^2+p_B(\omega_B-\omega_0)^2(公式3)\]公式3计算A、B两个区域的类间方差。
4.针对每一个灰度值,计算类间方差。选择方差最大的灰度值,作为阀值\(t\)。

您的打赏,是对我的鼓励
