• Variational Inference
  • 概述
  • 与MCMC算法比较
  • 贝叶斯统计
  • ELBO(Evidence Lower Bound)
  • ELBO和KL散度
  • 参考
• Vanilla VAE
  • 分布变换
  • VAE的传统理解

Variational Inference

论文：

《Variational Inference: A Review for Statisticians》

《A Tutorial on Variational Bayesian Inference》

《Stochastic Variational Inference》

《An Introduction to Variational Methods for Graphical Models》

概述

泛函/变分方面的基本知识可参见《数学狂想曲（十三）》。

Variational Inference实际上和变分法一样，是个很广泛的概念。但是在ML领域，由于主要用在贝叶斯统计的优化方面，因此又叫做Variational Bayesian Inference。这里只讨论后者。

在概率模型中，我们常常需要近似难以计算的概率分布，在贝叶斯统计中，所有的对于未知量的推断(inference)问题可以看做是对后验概率(posterior)的计算，而这一概率通常难以计算。我们可以利用MCMC算法（参见《机器学习（二十六）》）做近似，但是对于大量数据，MCMC算法计算较慢。变分推断(Variational Inference)就为我们提供了一种更快更简单的适用于大量数据的近似推断方法。

与MCMC算法比较

MCMC方法是利用马尔科夫链取样来近似后验概率，变分法是利用优化结果来近似后验概率，那么我们什么时候用MCMC，什么时候用变分法呢？

首先，MCMC相较于变分法计算上消耗更大，但是它可以保证取得与目标分布相同的样本，而变分法没有这个保证：它只能寻找到近似于目标分布一个密度分布，但同时变分法计算上更快，由于我们将其转化为了优化问题，所以可以利用诸如随机优化(stochastic optimization)或分布优化(distributed optimization)等方法快速的得到结果。所以当数据量较小时，我们可以用MCMC方法消耗更多的计算力但得到更精确的样本。当数据量较大时，我们用变分法处理比较合适。

另一方面，后验概率的分布形式也影响着我们的选择。比如对于有多个峰值的混合模型，MCMC可能只注重其中的一个峰而不能很好的描述其他峰值，而变分法对于此类问题即使样本量较小也可能优于MCMC方法。

---

https://www.zhihu.com/question/45196331

贝叶斯推断中为什么不能直接从posterior sampling而是要采用MCMC方法?

贝叶斯统计

贝叶斯统计模型一般包括三类变量：观测变量(observed variables, data)（记作X），未知参数（parameters）和潜变量（latent variables）。在贝叶斯推断中，参数和潜变量统称为不可观测变量(unobserved variables)（记作Z）。

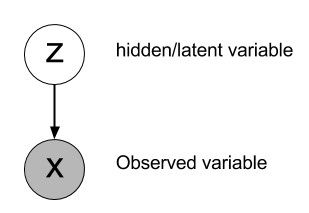
变分贝叶斯方法主要是两个目的:

1.近似不可观测变量的后验概率，以便通过这些变量作出统计推断。

2.对一个特定的模型（记作\(q(Z)\)），计算观测变量的边缘似然函数（或称为证据，evidence）的下界。使用ELBO选择模型：模型的ELBO值越高，则模型对数据拟合程度越好，该模型产生Data的概率也越高。我们对ELBO进行优化，从而得到最优的\(q(Z)\)。如果把\(q(Z)\)当成函数的话，这个问题就是标准的泛函优化问题。

ELBO(Evidence Lower Bound)

\[p(Z|X) = \frac{p(X|Z)p(Z)}{p(X)} = \frac{p(X|Z)p(Z)}{\int_Z p(X,Z)}\tag{Bayes’ Theorem}\] \[\begin{aligned} \log p(X) &= \log \int_Z p(X,Z) \\ &= \log \int_Z p(X,Z) \frac{q(Z)}{q(Z)} \\ &= \log \left( \mathbb{E}_q\left[\frac{p(X,Z)}{q(Z)}\right] \right)\\ &\geq \mathbb{E}_q\left[\log \frac{p(X,Z)}{q(Z)} \right] (\text{Jensen’s inequality})\\ &= \mathbb{E}_q\left[\log p(X,Z)\right] + H[Z] (\text{ELBO}) \end{aligned}\]

Jensen’s inequality的推导参见《机器学习（十）》。

通过上述变换，我们可以得到变分的下界ELBO。

ELBO和KL散度

\[\begin{align} \log P(x) &= \log P(x,z) - \log P(z|x) \\ &=\log\frac{P(x,z)}{q(z)} - \log\frac{P(z|x)}{q(z)} \\ &=\log P(x,z) - \log q(z) - \log\frac {P(z|x)}{q(z)} \\ &=\log P(x,z) - \log q(z) + \log\frac {q(z)}{P(z|x)} \\ \end{align}\]

等式两边同时对q(z)做期望，即：

\[\int q(z)\log P(x)dz =\int q(z)\log P(x,z)dz - \int q(z)\log q(z)dz + \int q(z)\log\frac{q(z)}{P(z|x)}dz\]

由于q(z)与P(x)无关，所以：

\[\int q(z)\log P(x)dz=\log P(x)\]

即：

\[\log P(x) = \underbrace{\int q(z)\log P(x,z)dz - \int q(z)\log q(z)dz}_{ELBO} + \underbrace{\int q(z)\log\frac{q(z)}{P(z|x)}dz}_{KL(q(z)||P(z|x))}\]

从上式可以看出，想让ELBO越大，则KL散度就要越小。即：最小化KL散度等价于最大化ELBO。

Variational Inference常用方法有Mean Field Method、混合高斯模型变分法等。

这些方法不但比较复杂，适用范围也有限，比如Mean Field Method，就要求所求解的问题满足Mean Field假设。

因此，下面提到的VAE，采用了另一种方法——使用神经网络求解分布优化问题。

总结一下：本章节的目的在于揭示为什么VAE需要最小化KL散度的原理，这也正是VAE名字中的Variational的由来。在后面的章节中，我们会看到VAE其实并没有用到常见的变分法，也没有积分这样的运算。

参考

https://zhuanlan.zhihu.com/p/49401976

变分推断

https://www.zhihu.com/question/41765860

如何简单易懂地理解变分推断(variational inference)？

http://nooverfit.com/wp/当变分推断（variational-inference）遇上神经网络，贝叶斯深度/

当变分推断（variational inference）遇上神经网络，贝叶斯深度学习以及Pytorch开源代码

https://blog.csdn.net/aws3217150/article/details/57072827

变分贝叶斯推断(Variational Bayes Inference)简介

https://www.cnblogs.com/yifdu25/p/8181185.html

变分推断（Variational Inference）

http://blog.huajh7.com/2013/03/06/variational-bayes/

变分贝叶斯算法理解与推导

https://www.cnblogs.com/yifdu25/p/8278986.html

ELBO与KL散度

https://blog.csdn.net/step_forward_ML/article/details/78077383

变分推断(Variational Inference)-mean field

https://mp.weixin.qq.com/s/olwyTaOGCugt-thgZm_3Mg

变分推断（Variational Inference）最新进展简述

https://mp.weixin.qq.com/s/1VSgqFXMt_xyT7Ugi3-Hhg

详解生成模型VAE的数学原理

https://zhuanlan.zhihu.com/p/96924903

变分推断与变分自编码器(VAE)

Vanilla VAE

变分自编码器（Variational Auto-Encoder，VAE）是Autoencoder的一种扩展。

论文：

《Auto-Encoding Variational Bayes》

Diederik P. Kingma，荷兰人，Univ. of Amsterdam博士（2017）。现为OpenAI科学家。VAE和Adam optimizer的发明者。
个人主页：
http://dpkingma.com

除了原始论文之外，以下综述也很有名：

《Tutorial on Variational Autoencoders》

《An Introduction toVariational Autoencoders》

代码：

https://github.com/keras-team/keras/blob/master/examples/variational_autoencoder.py

Keras官方提供的代码示例

研究者将常见的生成模型分为两种：一种是基于似然的模型，包括VAE及其变体、基于流的模型、以及自回归（autoregressive）模型，另一种是隐式生成模型，如生成对抗网络（GAN）。

以下部分主要摘自：

https://kexue.fm/archives/5253

变分自编码器（一）：原来是这么一回事

分布变换

通常我们会拿VAE跟GAN比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量Z生成目标数据X的模型，但是实现上有所不同。更准确地讲，它们是假设了Z服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型\(X=g(Z)\)，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的映射。

现在假设Z服从标准的正态分布，那么我就可以从中采样得到若干个\(Z_1, Z_2, \dots, Z_n\)，然后对它做变换得到\(\hat{X}_1 = g(Z_1),\hat{X}_2 = g(Z_2),\dots,\hat{X}_n = g(Z_n)\)，我们怎么判断这个通过f构造出来的数据集，它的分布跟我们目标数据集的分布是不是一样的呢？

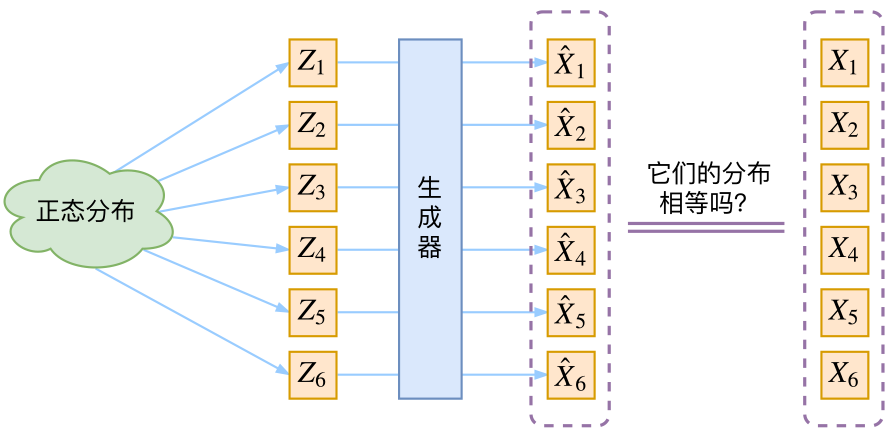
生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式。

有读者说不是有KL散度吗？当然不行，因为KL散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式，我们只有一批从构造的分布采样而来的数据\(\{\hat{X}_1,\hat{X}_2,\dots,\hat{X}_n\}\)，还有一批从真实的分布采样而来的数据\(\{X_1,X_2,\dots,X_n\}\)（也就是我们希望生成的训练集）。我们只有样本本身，没有分布表达式，当然也就没有方法算KL散度。

虽然遇到困难，但还是要想办法解决的。GAN的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧。而VAE则使用了一个精致迂回的技巧。

VAE的传统理解

首先我们有一批数据样本\(\{X_1,\dots,X_n\}\)，其整体用X来描述，我们本想根据\(\{X_1,\dots,X_n\}\)得到X的分布p(X)，如果能得到的话，那我直接根据p(X)来采样，就可以得到所有可能的X了（包括\(\{X_1,\dots,X_n\}\)以外的），这是一个终极理想的生成模型了。当然，这个理想很难实现，于是我们将分布改一改：

\[p(X)=\sum_Z p(X|Z)p(Z)\]

此时\(p(X\mid Z)\)就描述了一个由Z来生成X的模型，而我们假设Z服从标准正态分布，也就是\(p(Z)=\mathcal{N}(0,I)\)。如果这个理想能实现，那么我们就可以先从标准正态分布中采样一个Z，然后根据Z来算一个X，也是一个很棒的生成模型。接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下：

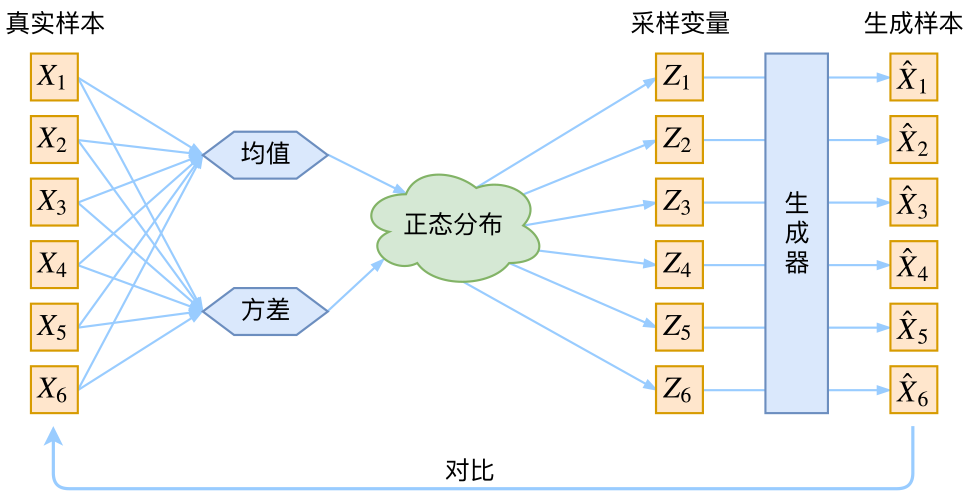
看出了什么问题了吗？如果像这个图的话，我们其实完全不清楚：究竟经过重新采样出来的\(Z_k\)，是不是还对应着原来的\(X_k\)，所以我们如果直接最小化\(\mathcal{D}(\hat{X}_k,X_k)^2\)（这里D代表某种距离函数）是很不科学的，而事实上你看代码也会发现根本不是这样实现的。