ML » 机器学习(十)——K-Means算法
2016-09-05 :: 5605 Words贝叶斯统计和规则化ML(续)
因为预测样本集和训练样本集的分布是独立的,因此上式又可写为:
\[p(y\mid x,S)=\int_\theta p(y\mid x,\theta)p(\theta\mid S)\mathrm{d}\theta\]这个公式又被称作后验预测分布(Posterior predictive distribution)。
\(p(\theta\mid S)\)可由前面的公式得到。
假若我们要求期望值的话,那么套用求期望的公式即可:
\[E[y\mid x,S]=\int_y yp(y\mid x,S)\mathrm{d}y\]由上可见,贝叶斯估计将\(\theta\)视为随机变量,\(\theta\)的值满足一定的分布,不是固定值,我们无法通过计算获得其值,只能在预测时计算积分。
上述贝叶斯估计方法,虽然公式合理优美,但后验概率\(p(\theta\mid S)\)通常是很难计算的,因为它是\(\theta\)上的高维积分函数。
观察\(p(\theta\mid S)\)的公式,在分母\(P(S)\)一定的情况下,分子越大则值越大,也就是\(p(\theta\mid S)\)的概率越大。
因此,可得如下算法:
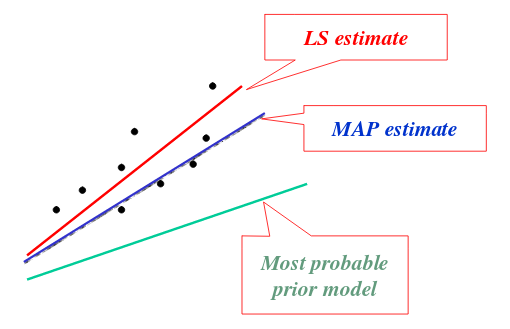
\[\theta_{MAP}=\arg\max_\theta\left(\prod_{i=1}^mp(y^{(i)}\mid x^{(i)},\theta)\right)p(\theta)\]这个算法叫做最大后验概率估计(maximum a posteriori)。
和ML相比,MAP算法只是在最后多了一项\(p(\theta)\)。通常使用中,我们认为\(p(\theta)\)符合\(\theta\sim N(0,\tau^2I)\)。
由于\(p(\theta)\)实际上就是先验分布,它会对最后结果进行一定的修正。因此,实际上最大后验概率估计相对于最大似然估计来说,较容易克服过度拟合的问题。
参见:
http://www.cs.cornell.edu/courses/cs5540/2010sp/lectures/Lec9.Estimation-continued.pdf
Statistical Estimation: Least Squares, Maximum Likelihood and Maximum A Posteriori Estimators
https://mp.weixin.qq.com/s/XnsbCb7H9jHmJ4dV9p2Oug
频率学派还是贝叶斯学派?聊一聊机器学习中的MLE和MAP
https://mp.weixin.qq.com/s/dQxN46wEbFrpvV369uOHdA
详解最大后验概率估计(MAP)的理解
K-Means算法
聚类算法属于无监督学习算法的一种。它的训练样本中只有\(x^{(i)}\),而没有\(y^{(i)}\)。聚类的目的是找到每个样本x潜在的类别y,并将同类别y的样本x放在一起,形成一个聚类(clusters)。样本\(x^{(i)}\)所属的聚类用\(c^{(i)}\)表示。
K-Means算法的步骤如下:
1.随机选取k个聚类质心点(cluster centroids)\(\mu_1,\dots,\mu_k\)
2.重复下面过程直到收敛 {对于每一个样例i,计算其应该属于的聚类:\(c^{(i)}:=\arg\min_j\|x^{(i)}-\mu_j\|^2\)
对于每一个聚类j,重新计算该聚类的质心:\(\mu_j:=\frac{\sum_{i=1}^m1\{c^{(i)}=j\}x^{(i)}}{\sum_{i=1}^m1\{c^{(i)}=j\}}\)。}
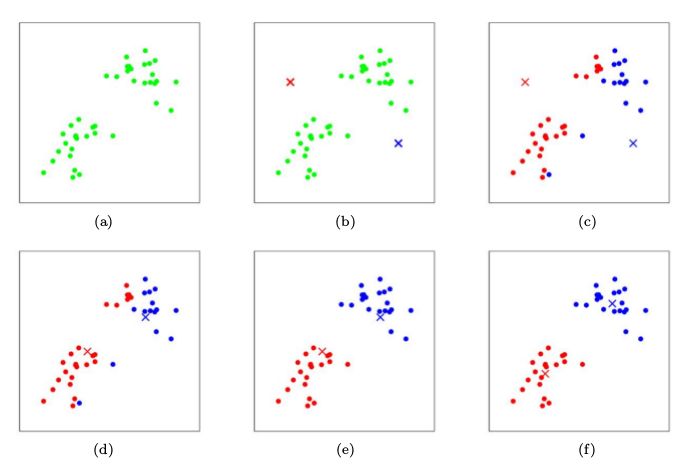
其中,k是我们事先定义的聚类个数。下图展示了对n个样本点进行K-means聚类的效果,这里k取2。
K-means算法面对的第一个问题是如何保证收敛。前面的算法中强调结束条件就是收敛,可以证明的是K-means完全可以保证收敛性。下面我们定性的描述一下收敛性,我们定义畸变函数(distortion function)如下:
\[J(c,\mu)=\sum_{i=1}^m\|x^{(i)}-\mu_{c^{(i)}}\|^2\]J函数表示每个样本点到其质心的距离平方和。K-means算法的目的是要将J调整到最小。假设当前J没有达到最小值,那么首先可以固定每个类的质心\(\mu_j\),调整每个样例的所属的类别\(c^{(i)}\)来让J函数减小,同样,固定\(c^{(i)}\),调整每个类的质心\(\mu_j\),也可以使J减小。 这两个过程就是内循环中使J单调递减的过程。当J递减到最小时,\(\mu\)和c也同时收敛。(在理论上,可以有多组不同的\(\mu\)和c值,能够使得J取得最小值,但这种现象实际上很少见。)
由于畸变函数J是非凸函数,意味着我们不能保证算法取得的最小值是全局最小值,也就是说k-means对质心初始位置的选取比较敏感。但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优,那么可以选取不同的初始值跑多遍k-means,然后取其中最小的J对应的\(\mu\)和c输出。
参考:
http://www.csdn.net/article/2012-07-03/2807073-k-means
深入浅出K-Means算法
http://www.cnblogs.com/leoo2sk/archive/2010/09/20/k-means.html
k均值聚类(K-means)
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006910.html
K-means聚类算法
https://mp.weixin.qq.com/s/86MlCMKAG0ax3gvfsgmYtg
K-Means聚类算法详解
https://mp.weixin.qq.com/s/Sl3lTS1zvq0BgAayAUcOXg
K-Means实战与调优详解
https://mp.weixin.qq.com/s/6ErpBtVg0r2dhsBGbIkvDg
Bisecting K-Means算法
https://mp.weixin.qq.com/s/oAvNzxENTfaxUkSRypCo1g
K-Means算法的10个有趣用例
https://zhuanlan.zhihu.com/p/45408671
K-Means小谈
聚类结果的评价
可考虑用以下几个指标来评价聚类效果:
1.聚类中心之间的距离。距离值大,通常可考虑分为不同类。
2.聚类域中的样本数目。样本数目少且聚类中心距离远,可考虑是否为噪声。
3.聚类域内样本的距离方差。方差过大的样本可考虑是否属于这一类。
Elbow Method
K-means算法中,K值的选取除了依赖领域知识之外,还可以采用Elbow Method(肘部原则)来确定。
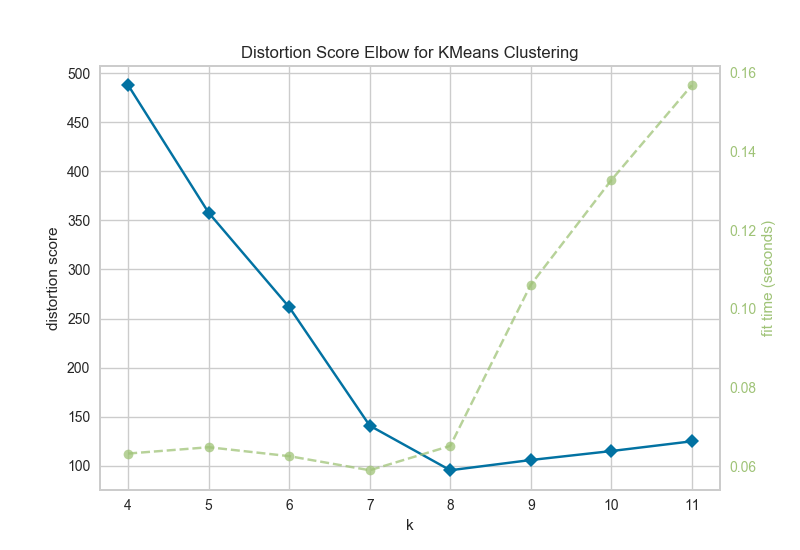
上图中的蓝线是畸变率,数值越低越好,而绿线是计算时间,也是数值越低越好。可以看出K=8的时候,效果最佳。实际上即使只有一根线,我们也可以判断K取值的优劣:折线的斜率在K=8处,变化较大,形如人的肘部,故名。
参考:
https://www.scikit-yb.org/en/latest/api/cluster/elbow.html
Elbow Method
https://bl.ocks.org/rpgove/0060ff3b656618e9136b
Using the elbow method to determine the optimal number of clusters for k-means clustering
高斯混合模型和EM算法
本篇讨论使用期望最大化算法(Expectation-Maximization)进行密度估计(density estimation)。
从上面的讨论可以形象的看出,聚类问题实际就是在数据集上,找出一个个数据密度较高的“圆圈”。我们可以反过来思考这个问题:如果我们已知圆圈的圆心和半径,那么也可以根据圆心、半径以及样本分布模型,来随机生成这些数据。显然,这和前一种做法在效果上是等效的。
首先我们假设样本数据满足联合概率分布
\[p(x^{(i)},z^{(i)})=p(x^{(i)}\mid z^{(i)})p(z^{(i)})\tag{5}\]其中,\(z^{(i)}\sim Multinomial(\phi)\)(这里的\(\phi_j=p(z^{(i)}=j)\),因此\(\phi_j\ge 0,\sum_{j=1}^k\phi_j=1\)),\(z^{(i)}\)的值为k个聚类之一。
假定\(x^{(i)}\mid z^{(i)}=j\sim \mathcal{N}(\mu_j,\Sigma_j)\),则该模型被称为高斯混合模型(mixture of Gaussians model)。
整个模型简单描述为对于每个样例\(x^{(i)}\),我们先从k个类别中按多项分布抽取一个\(z^{(i)}\),然后根据\(z^{(i)}\)所对应的k个多值高斯分布中的一个生成样例\(x^{(i)}\)。注意的是这里的\(z^{(i)}\)是隐含的随机变量(latent random variables)。
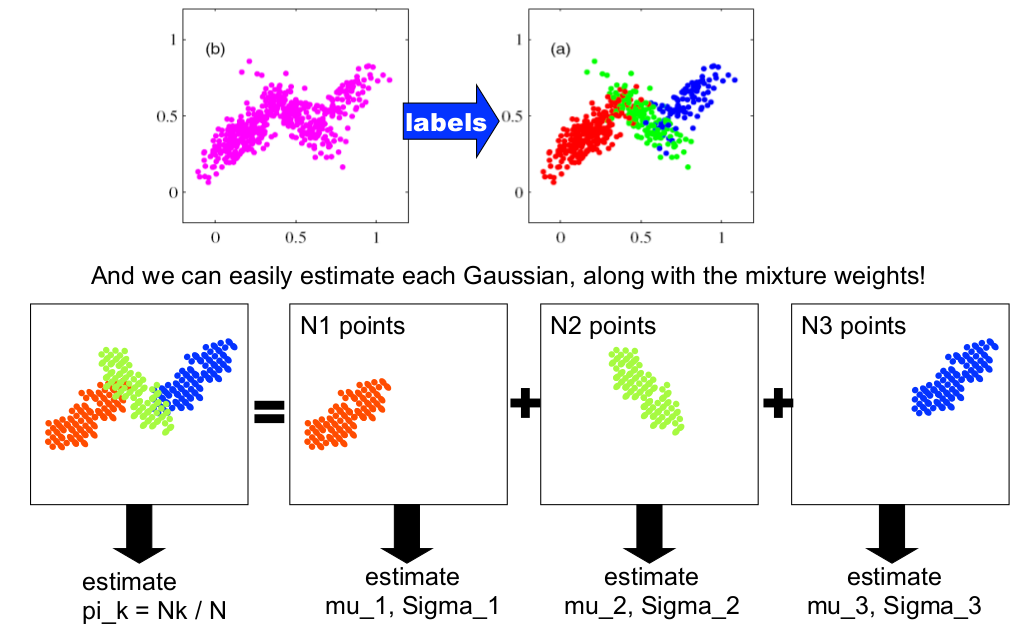
因此,由全概率公式可得:
\[p(x^{(i)};\phi,\mu,\Sigma)=\sum_{z^{(i)}=1}^kp(x^{(i)}\mid z^{(i)};\mu,\Sigma)p(z^{(i)};\phi)\tag{6}\]该模型的对数化似然函数为:
\[\ell(\phi,\mu,\Sigma)=\sum_{i=1}^m\log p(x^{(i)};\phi,\mu,\Sigma)=\sum_{i=1}^m\log \sum_{z^{(i)}=1}^kp(x^{(i)}\mid z^{(i)};\mu,\Sigma)p(z^{(i)};\phi)\]这个式子的最大值不能通过求导数为0的方法解决的,因为它不是close form。(多项分布的概率密度函数包含阶乘运算,不满足close form的定义。)
为了简化问题,我们假设已经知道每个样例的\(z^{(i)}\)值。这实际上就转化成《机器学习(二)》所提到的GDA模型。和之前模型的区别在于,\(z^{(i)}\)是多项分布,而且每个聚类的\(\Sigma\)都不相同,但结论是类似的。
这里的直接推导非常复杂,可参考以下文章:
http://www.cse.psu.edu/~rtc12/CSE586/lectures/EMLectureFeb3.pdf
上面这篇文章比较直观,比Andrew讲义的Problem Set详细的多。然而Andrew这样写是有原因的,在后面的章节,借助Jensen不等式,Andrew给出一个更简单且一般化的推导过程。
接下来的问题就是:\(z^{(i)}\)的值我们是不知道的,该怎么办呢?
EM算法的思路是:
1.猜测\(z^{(i)}\)的值。(这一步即所谓的Expectation,简称E-Step。)
2.最大化计算,以更新模型的参数。(这一步即所谓的Maximization,简称M-Step。)
具体到这里就是:
Repeat until convergence {
(E-step) For each i, j:
\[w_j^{(i)}:=p(z^{(i)}=j\mid x^{(i)};\phi,\mu,\Sigma)\](M-step) Update the parameters:
\(\phi_j:=\frac{1}{m}\sum_{i=1}^mw_j^{(i)}\)
\(\mu_j:=\frac{\sum_{i=1}^mw_j^{(i)}x^{(i)}}{\sum_{i=1}^mw_j^{(i)}}\)
\(\Sigma_j:=\frac{\sum_{i=1}^mw_j^{(i)}(x^{(i)}-\mu_j)(x^{(i)}-\mu_j)^T}{\sum_{i=1}^mw_j^{(i)}}\)}
E-Step中,根据贝叶斯公式可得:
\[p(z^{(i)}=j\mid x^{(i)};\phi,\mu,\Sigma)=\frac{p(x^{(i)}\mid z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{\sum_{l=1}^kp(x^{(i)}\mid z^{(i)}=l;\mu,\Sigma)p(z^{(i)}=l;\phi)}\]将假设模型的各概率密度函数代入上式,即可计算得到\(w_j^{(i)}\)。
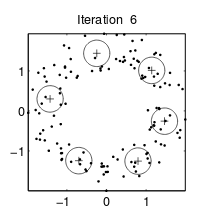
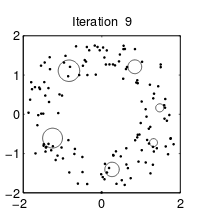
相比于K-means算法,GMM算法中的\(z^{(i)}\)是个概率值,而非确定值,因此也被称为soft assignments。
K-means算法各个聚类的特征都是一样的,也就是“圆圈”的半径一致。而GMM算法的“圆圈”半径可以不同。如下面两图所示:
 |
 |
| K-means算法 | GMM算法 |
注意:这里的圆圈是先验估计值,它和最后的聚类形状无关。
GMM算法结果也是局部最优解。对其他参数取不同的初始值进行多次计算同样适用于GMM算法。

您的打赏,是对我的鼓励
