• Latent Dirichlet Allocation
  • 马氏链及其平稳分布
  • MCMC
  • Gibbs Sampling
  • Unigram Model
  • PLSA
  • LDA

Latent Dirichlet Allocation

Latent Dirichlet Allocation，简称LDA。注意不要和Linear Discriminant Analysis搞混了。

这方面的文章，首推rickjin（靳志辉）写的《LDA数学八卦》一文。全文篇幅长达55页，我实在没有能力写的比他更好，因此这里就做一个摘要好了。

靳志辉，北京大学计算机系计算语言所硕士，日本东京大学情报理工学院统计自然语言处理方向博士。2008年加入腾讯，主要工作内容涉及统计自然语言处理和大规模并行机器学习工具的研发工作。目前为腾讯社交与效果广告部质量研发中心总监，主要负责腾讯用户数据挖掘、精准广告定向、广告语义特征挖掘、广告转化率预估等工作。
他写的另一篇文章《正态分布的前世今生》，也是统计界著名的科普文，非常值得一看。

马氏链及其平稳分布

Markov chain的定义如下：

\[P(X_{t+1}=x\mid X_t, X_{t-1}, \cdots) =P(X_{t+1}=x\mid X_t)\]

即状态转移的概率只依赖于前一个状态的随机过程。

上面是1阶Markov过程的定义。类似的还可以定义n阶Markov过程，即状态转移的概率只依赖于前n个状态的随机过程。

Andrey(Andrei) Andreyevich Markov，1856~1922，俄国数学家。圣彼得堡大学博士，导师Pafnuty Chebyshev。最早研究随机过程的数学家之一。圣彼得堡学派的第二代领军人物，俄罗斯科学院院士。
虽然现在将随机过程（stochastic process）划为数理统计科学的一部分，然而在19世纪末期，相关的研究者在学术界分属两个不同的团体。其中最典型的就是英国的剑桥学派（Pearson、Fisher等）和俄国的圣彼得堡学派（Chebyshev、Markov等）。因此将Markov称为统计学家是非常错误的观点。

有的课本里给的马氏链的定义为：在已知它目前状态(现在)条件下，它未来的演变(将来)不依赖于它以往的演变(过去)。
显然这个定义和上面的定义是等价的，但由此引入的历史无关性的概念却颇有迷惑性。从公式来看，马氏链不但不是历史无关，而且历史信息还是该模型的精髓，所谓的历史无关，仅仅指的是太老的历史就被忽略了。

一些非周期的马氏链，经过若干次的状态转移之后，其状态概率会收敛到一个特定的数值，即平稳分布（stationary distribution）。

如各参考文献所示，这里一般会举社会学上的人口分层问题，引出马氏链的极限和平稳分布的概念。这里要特别注意马氏链收敛定理以及它的具体含义。

细致平稳条件：如果非周期马氏链的转移矩阵P和分布\(\pi(x)\)满足

\[\pi(i)P_{ij} = \pi(j)P_{ji} \quad\quad \text{for all} \quad i,j\]

则\(\pi(x)\)是马氏链的平稳分布，上式被称为细致平稳条件(detailed balance condition)。

满足细致平稳条件的马氏链，其后续状态都是平稳分布状态，不会再改变。

注:细致平稳条件，比平稳分布的条件要强，因此它是平稳分布的充分条件，而非必要条件。

参考：

http://blog.csdn.net/lanchunhui/article/details/50451620

重温马尔科夫随机过程

http://blog.csdn.net/pipisorry/article/details/46618991

马尔科夫模型

MCMC

对于给定的概率分布\(p(x)\)，我们希望能有便捷的方式生成它对应的样本。由于马氏链能收敛到平稳分布，于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为P的马氏链，使得该马氏链的平稳分布恰好是\(p(x)\)，那么我们从任何一个初始状态\(x_0\)出发沿着马氏链转移，得到一个转移序列\(x_0, x_1, x_2, \cdots x_n, x_{n+1}\cdots\)，如果马氏链在第n步已经收敛了，于是我们就得到了\(\pi(x)\)的样本\(x_n, x_{n+1}\cdots\)。

Markov Chain Monte Carlo算法的核心是引入一个参数\(\alpha(i,j)\)使得一个普通的马氏链，变成一个满足细致平稳条件的马氏链。即：

\[p(i) \underbrace{q(i,j)\alpha(i,j)}_{Q'(i,j)} = p(j) \underbrace{q(j,i)\alpha(j,i)}_{Q'(j,i)} \quad\]

以上即为Metropolis算法。

Nicholas Constantine Metropolis，1915~1999，希腊裔美籍物理学家。芝加哥大学博士，反复供职于Los Alamos和芝加哥大学。（其实也就这俩地方，只不过这边干几年到那边去，那边教几年书再回这边来，这么进进出出好几个来回而已）“曼哈顿计划”的主要科学家之一，战后主持MANIAC计算机的研制。

\(\alpha\)的大小，决定了马氏链的收敛速度。\(\alpha\)越大，收敛越快。因此又有Metropolis–Hastings算法，其关键公式为：

\[\alpha(i,j) = \min\left\{\frac{p(j)q(j,i)}{p(i)q(i,j)},1\right\}\]

Wilfred Keith Hastings，1930~2016，美国统计学家，多伦多大学博士，维多利亚大学教授。

除了MCMC之外，常用的采样方法还有Hamiltonian Monte Carlo（HMC）。

参考：

https://zhuanlan.zhihu.com/p/32315762

如何简单地理解“哈密尔顿蒙特卡洛 (HMC)”？

https://mp.weixin.qq.com/s/BZh3-jk2LNK55jKGJXQgjw

蚂蚁金服：如何训练可自动调整负样本采样器？

Gibbs Sampling

这个算法虽然以Gibbs命名，但却是Geman兄弟于1984年研究Gibbs random field时，发现的算法。

Josiah Willard Gibbs，1839~1903，美国科学家。他在物理、化学和数学方面都有重大理论贡献。耶鲁大学博士和教授。统计力学的创始人。

Donald Jay Geman，1943年生，美国数学家。美国西北大学博士，布朗大学教授。随机森林算法的早期研究者之一。

Stuart Alan Geman，1949年生，美国数学家。MIT博士，约翰霍普金斯大学教授。美国科学院院士。最早将Markov random field（MRF）应用于机器视觉和机器学习。

因为高维空间中，沿坐标轴方向上的两点之间的转移，满足细致平稳条件。因此，Gibbs Sampling的核心就是沿坐标轴循环迭代采样，该算法收敛之后的采样点即符合指定概率分布。

这里需要特别指出的是，Gibbs Sampling比Metropolis–Hastings算法高效的原因在于：Gibbs Sampling每次沿坐标轴的转移是必然会被接受的，即\(\alpha=1\)。

参考：

https://mp.weixin.qq.com/s/ogSrwfDxXP0rCkP6diexdA

吉布斯——热力学大师与统计物理奠基人

Unigram Model

假设我们的词典中一共有V个词\(v_1,v_2,\cdots v_V\)，那么最简单的Unigram Model是定义一个V面的骰子，每抛一次骰子，抛出的面就对应产生一个词。

频率学派的Unigram Model如下图：

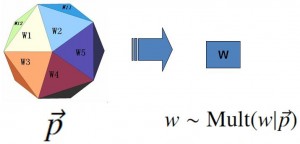
贝叶斯学派的Unigram Model如下图：

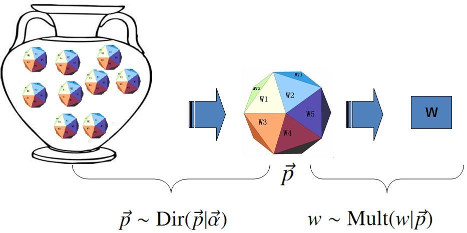
这里使用Dirichlet分布的原因在于，数据采用多项分布，而Dirichlet分布正好是多项分布的共轭先验分布。

\[Dir(\overrightarrow{p}\mid \overrightarrow{\alpha})+MultCount(\overrightarrow{n})=Dir(\overrightarrow{p}\mid \overrightarrow{\alpha}+\overrightarrow{n})\]

和wiki上对Dirichlet分布的pdf函数的描述（参见《数学狂想曲（二）》中的公式1）不同，rickjin在这里采用了如下定义：

\[Dir(\overrightarrow{p}\mid \overrightarrow{\alpha})= \frac{1}{\Delta(\overrightarrow{\alpha})} \prod_{k=1}^V p_k^{\alpha_k -1}， \quad \overrightarrow{\alpha}=(\alpha_1, \cdots, \alpha_V)\]

其中：

\[\Delta(\overrightarrow{\alpha}) = \int \prod_{k=1}^V p_k^{\alpha_k -1} d\overrightarrow{p}\]

可以看出两种描述中的\(\mathrm{B}(\boldsymbol\alpha)\)和\(\Delta(\overrightarrow{\alpha})\)是等价的。

下面我们来证明这个结论，即：

\[\mathrm{B}(\boldsymbol\alpha)=\int \prod_{k=1}^V p_k^{\alpha_k -1} d\overrightarrow{p}\tag{1}\]

证明：这里为了简化问题，令V=3。则根据《数学狂想曲（二）》中的公式1可得：

\[Dir(\overrightarrow{p}\mid \overrightarrow{\alpha})= \frac{1}{\mathrm{B}(\alpha_1,\alpha_2,\alpha_3)} p_1^{\alpha_1 -1}p_2^{\alpha_2 -1}p_3^{\alpha_3 -1}\]

对该pdf进行积分：

\[\iiint\frac{1}{\mathrm{B}(\alpha_1,\alpha_2,\alpha_3)}p_1^{\alpha_1 -1}p_2^{\alpha_2 -1}p_3^{\alpha_3 -1}\mathrm{d}p_1\mathrm{d}p_2\mathrm{d}p_3=\frac{1}{\mathrm{B}(\alpha_1,\alpha_2,\alpha_3)}\int p_1^{\alpha_1 -1}p_2^{\alpha_2 -1}p_3^{\alpha_3 -1}\mathrm{d}\overrightarrow{p}\]

由pdf的定义可知，上面的积分值为1。

因此：

\[\mathrm{B}(\alpha_1,\alpha_2,\alpha_3)=\int p_1^{\alpha_1 -1}p_2^{\alpha_2 -1}p_3^{\alpha_3 -1}\mathrm{d}\overrightarrow{p}\]

证毕。

从上面的证明过程，可以看出公式1并不是恒等式，而是在Dirichlet分布下才成立的等式。这也是共轭先验分布能够简化计算的地方。

PLSA

Probabilistic Latent Semantic Analysis是Thomas Hofmann于1999年在UCB读博期间提出的算法。

原文：

https://dslpitt.org/uai/papers/99/p289-hofmann.pdf

示意图：

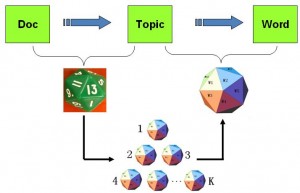
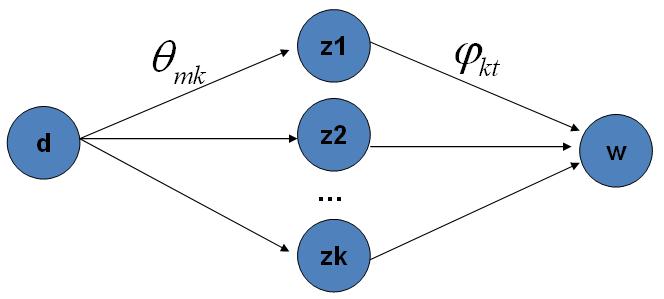
PLSA将生成文档的过程，分为两个步骤：

1.生成文档的主题。（doc->topic）

2.根据主题生成相关的词.（topic->word）

第m篇文档\(d_m\)中的每个词的生成概率为：

\[p(w\mid d_m) = \sum_{z=1}^K p(w\mid z)p(z\mid d_m) = \sum_{z=1}^K \varphi_{zw} \theta_{mz}\]

LDA

利用贝叶斯学派的观点改造PLSA，可得：

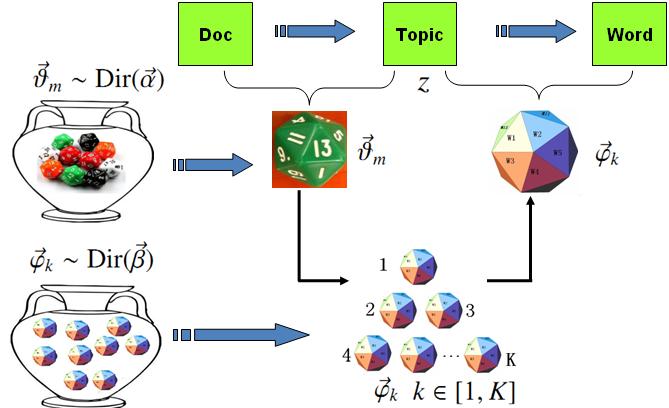
LDA生成模型包含两个过程：

1.生成第m篇文档中的所有词对应的topics。

\[\overrightarrow{\alpha}\xrightarrow[Dirichlet]{} \overrightarrow{\theta}_m \xrightarrow[Multinomial]{} \overrightarrow{z}_{m}\]

2.K个由topics生成words的独立过程。

\[\overrightarrow{\beta} \xrightarrow[Dirichlet]{} \overrightarrow{\varphi}_k \xrightarrow[Multinomial]{} \overrightarrow{w}_{(k)}\]

因此，总共就是\(M+K\)个Dirichlet-Multinomial共轭结构。

LDA的Gibbs Sampling图示：

LDA模型的目标有两个：

训练模型：估计模型中的参数：\(\overrightarrow{\varphi}_1, \cdots, \overrightarrow{\varphi}_K\)和\(\overrightarrow{\theta}_1, \cdots, \overrightarrow{\theta}_M\)。

由于参数\(\overrightarrow{\theta}_m\)是和训练语料中的每篇文档相关的，对于我们理解新的文档并无用处，所以工程上最终存储LDA模型时，一般没有必要保留。

这一步实际上是一个聚类的过程。