• 概述
• IEEE 754
  • Microsoft Binary Format
• 浮点数取整
• Distiller
• Conservative vs. Aggressive
• INT量化
• UINT量化
• bfloat16
• Flexpoint

概述

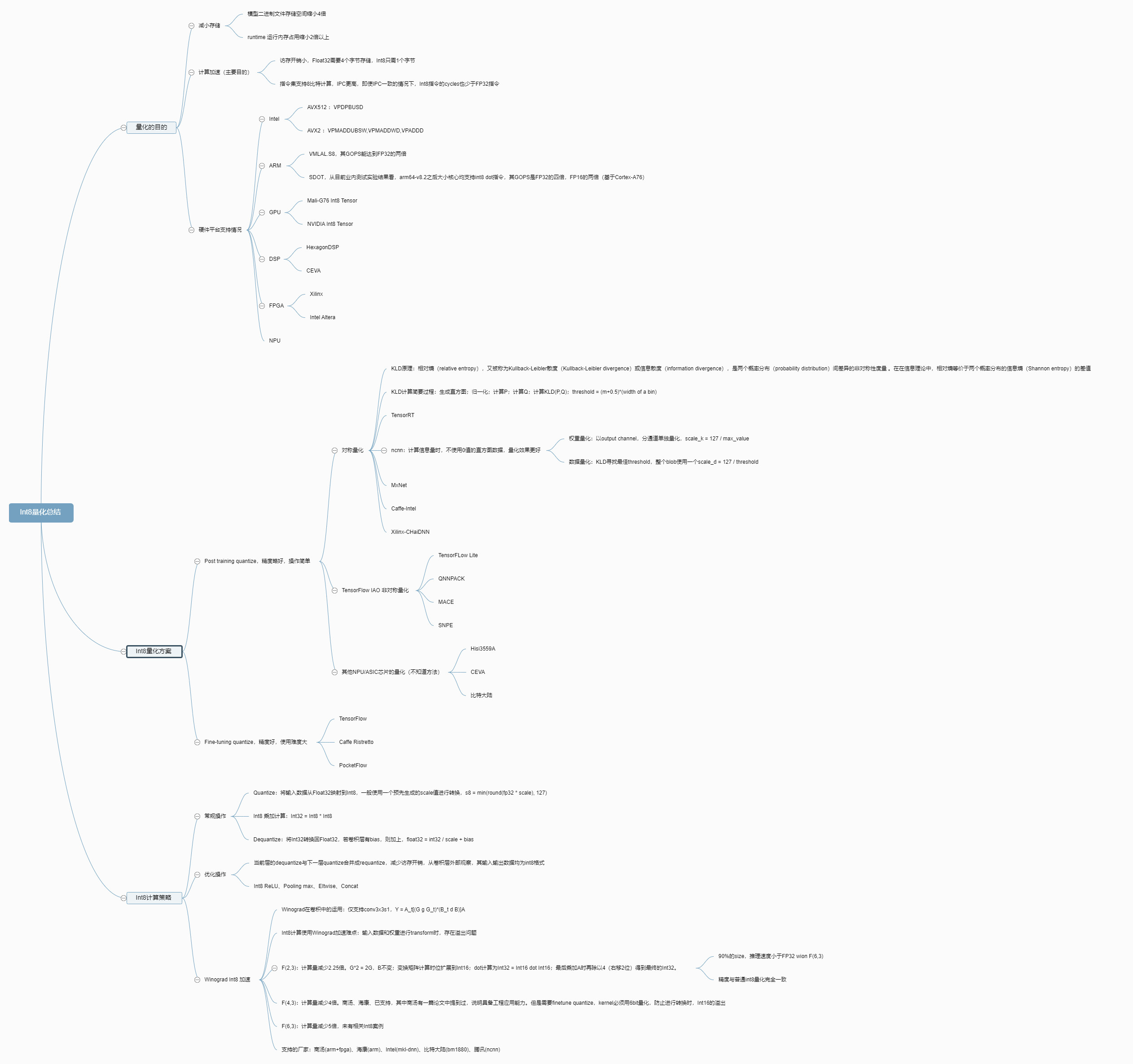
NN的量化计算是近来NN计算优化的方向之一。相比于传统的浮点计算，整数计算无疑速度更快，而NN由于自身特性，对单点计算的精确度要求不高，且损失的精度还可以通过retrain的方式恢复大部分，因此通常的科学计算的硬件（没错就是指的GPU）并不太适合NN运算，尤其是NN Inference。

传统的GPU并不适合NN运算，因此Nvidia也好，还是其他GPU厂商也好，通常都在GPU中又集成了NN加速的硬件，因此虽然商品名还是叫做GPU，但是工作原理已经有别于传统的GPU了。

这方面的文章以Xilinx的白皮书较为经典：

https://china.xilinx.com/support/documentation/white_papers/c_wp486-deep-learning-int8.pdf

利用Xilinx器件的INT8优化开展深度学习

IEEE 754

在开始进一步介绍之前，我们首先回顾一下浮点数在硬件上的表示方法。其中最重要的就是IEEE 754标准。

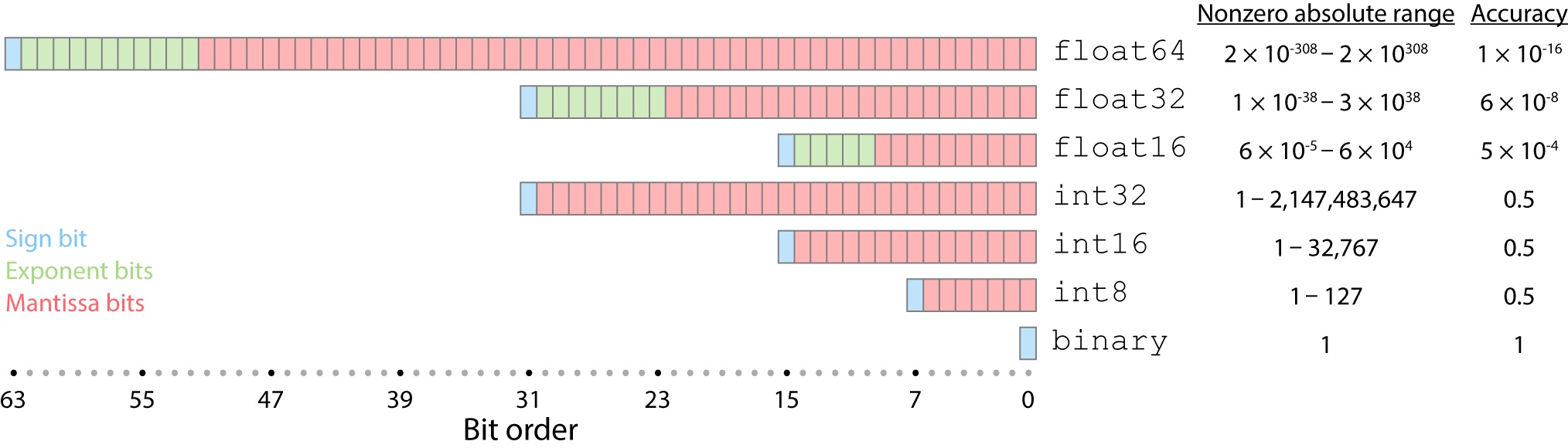
目前，clang编译器已经原生支持FP16，但gcc还不行，不过可以用以下项目支持之：

http://half.sourceforge.net/

half - IEEE 754-based half-precision floating point library

显然，Significand的位数决定Accuracy，而Exponent的位数决定Dynamic Range。

上溢：超出所能表示的最大数（\(\to \infty\)）。

下溢：超出所能表示的最小数（\(\to 0\)）。

除了IEEE 754之外，还有IBM hexadecimal floating point。相比于IEEE 754，IBM格式的Significand位数多一些，而Exponent的位数少一些。

denorm：denormalized number

一个正规数是指指数位非零的数，而非正规数（denorm）是指指数位全为零的数。

C++17以后有了更多的浮点数表示方法：

Literal         Printed value
58.             58
4e2             400
123.456e-67     1.23456e-65
123.456e-67f    0
.1E4f           1000
0x10.1p0        16.0625
0x1p5           32
0x1e5           485
3.14'15'92      3.14159
1.18e-4932l     1.18e-4932
3.4028234e38f   340282346638528859811704183484516925440
3.4028234e38    340282339999999992395853996843190976512
3.4028234e38l   340282339999999999995912555211526242304

C++23添加了std::float16_t、std::float32_t、std::float64_t、std::float128_t、std::bfloat16_t等类型。

google的ml_dtypes库，提供了float8_e5m2、float8_e4m3fn、int4等类型的支持。

https://github.com/jax-ml/ml_dtypes

参考：

https://en.wikipedia.org/wiki/IEEE_754

http://blog.codinglabs.org/articles/trouble-of-x86-64-platform.html

x86-64体系下一个奇怪问题的定位

Microsoft Binary Format

MS早期的Basic产品中使用了一种特殊的浮点表示方法，被称作Microsoft Binary Format（1975年）。与后来的浮点标准主要由硬件厂商主导不同，这时的浮点运算还是以软件的形式运行在定点运算单元上。

浮点数取整

浮点数取整的方法一般有：

• 截断取整。

• 向上/向下取整。

• 四舍五入。

• 四舍六入五成双，也称为向偶数取整。例子：3.5->4, 4.5->4.

一般来说，后两种用的较多，尤其是最后一种。

Distiller

https://nervanasystems.github.io/distiller/index.html

Intel AI Lab推出的Distiller是一个关于模型压缩、量化的工具包。这里是它的文档，总结了业界主要使用的各种方法。

参考：

https://mp.weixin.qq.com/s/A5ka8evElmcuHdowof7kww

Intel发布神经网络压缩库Distiller：快速利用前沿算法压缩PyTorch模型

Conservative vs. Aggressive

Quantization主要分为两大类：

1.”Conservative” Quantization。这里主要指不低于INT8精度的量化。

实践表明，由于NN训练时采用的凸优化算法，其最终结果一般仅是局部最优。因此，即便是两次训练（数据集、模型完全相同，样本训练顺序、参数初始值随机）之间的差异，通常也远大于FP64的精度。所以，一般而言，FP32对于模型训练已经完全够用了。

FP16相对于FP32，通常会有不到1%的精度损失。即使是不re-train的INT8，通常也只有3%～15%的精度损失。因此这类量化被归为”Conservative” Quantization。其特点是完全采用FP32的参数进行量化，或者在此基础上进行re-train。

1.”Aggressive” Quantization。这里指的是INT4或更低精度的量化。

这种量化由于过于激进，re-train也没啥大用，因此必须从头训练。而且由于INT4表达能力有限，模型结构也要进行一定的修改，比如增加每一层的filter的数量。

INT量化

论文：

《On the efficient representation and execution of deep acoustic models》

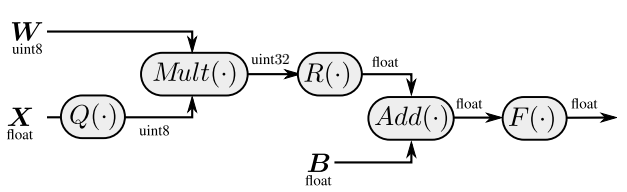
一个浮点数包括底数和指数两部分。将两者分开，就得到了一般的INT量化。

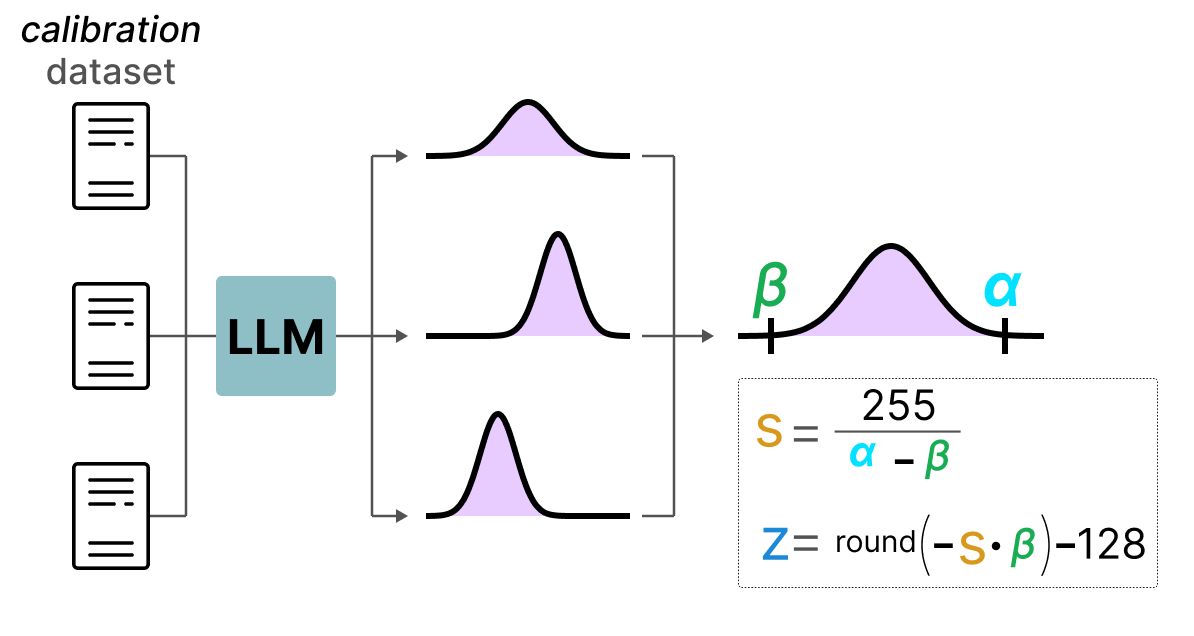
量化的过程一般如下：

1.使用一批样本进行推断，记录下每个layer的数值范围。

2.根据该范围进行量化。

量化的方法又分为两种：

1）直接使用浮点数表示中的指数。也就是所谓的fractional length，相当于2的整数幂。

2）使用更一般的scale来表示。这种方式的精度较高，但运算量稍大。

量化误差过大，一般可用以下方法减小：

1.按照每个channel的数值范围，分别量化。

2.分析weight、bias，找到异常值，并消除之。这些异常值通常是由于死去的神经元所导致的误差无法更新造成的。

如何确定每个layer的数值范围，实际上也有多种方法：

1.取整批样本在该layer的数值范围的并集，也就是所有最大（小）值的极值。

2.取所有最大（小）值的平均值。

UINT量化

论文：

《Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference》

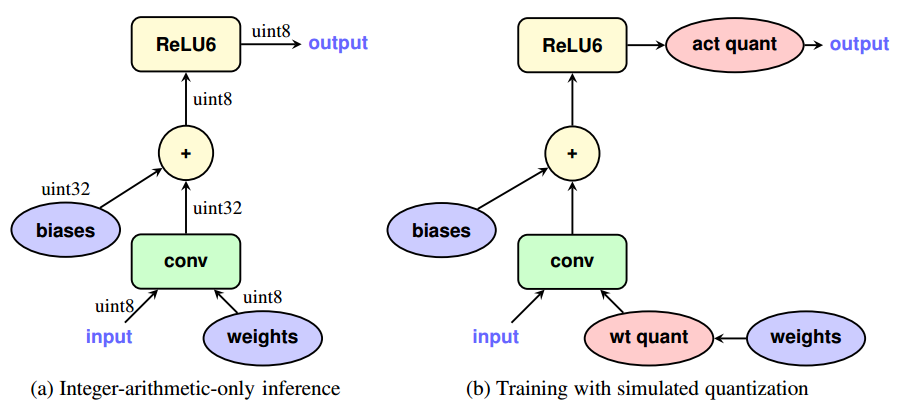
UINT量化使用bias将数据搬移到均值为0的区间。

r为fp32表示；q则是low-bit(如int8)表示；S是自low-bit（int8）到fp32的scale；Z为零点shift，用于使q的某数值对应于r中的0.0。

对于矩阵乘法来说：

则：

其中，\(M=\frac{S_1S_2}{S_3}\)。如果令\(S_3=S_1S_2\)，则上述运算将全部转为整数运算。

这篇论文的另一个贡献在于：原先的INT8量化是针对已经训练好的模型。而现在还可以在训练的时候就进行量化——前向计算进行量化，而反向的误差修正不做量化。这也就是所谓的训练中量化(Quantization Aware Training)。

与之相对的则是训练后量化(Post training quantization)。

tf.quantization.fake_quant_XXXX系列API可用于前向计算时的量化。

Fake quant之所以叫伪量化，是因为虽然可量化weights/activations，但不是真正意义上的量化，即变量类型还是floating point，而不是integer。

bfloat16

bfloat16是Google针对AI领域的特殊情况提出的浮点格式。目前已有Intel的AI processors和Google的TPU，提供对该格式的原生支持。

上图比较了bfloat16和IEEE fp32/fp16的差异。可以看出bfloat16有如下特点：

1.bfloat16可以直接截取float32的前16位得到，所以在float32和bfloat16之间进行转换时非常容易。

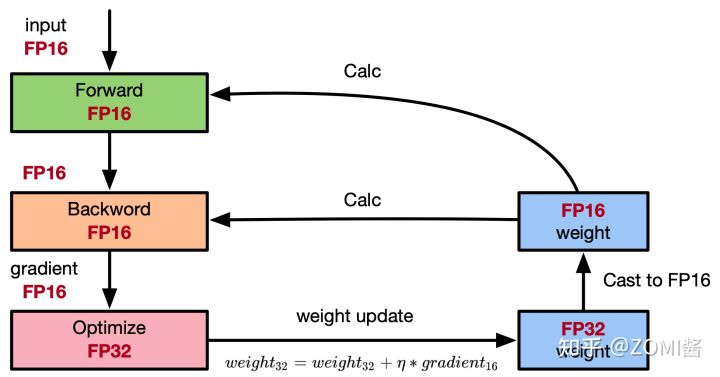
2.bfloat16的Dynamic Range比float16大，不容易下溢。这点在training阶段更为重要，梯度一般都挺小的，一旦下溢变成0，就传递不了了。

3.bfloat16既可以用于训练又可以用于推断。Amazon也证明Deep Speech模型使用BFloat的训练和推断的效果都足够好。Uint8在大部分情况下不能用于训练，只能用于推断。

论文：

《Mixed Precision Training》

AMP：Automatic Mixed Precision

参考：

https://www.zhihu.com/question/275682777

如何评价Google在TensorFlow中引入的bfloat16数据类型？

https://zhuanlan.zhihu.com/p/56114254

PAI自动混合精度训练—TensorCore硬件加速单元在阿里PAI平台落地应用实践

https://mp.weixin.qq.com/s/zBtpwrQ5HtI6uzYOx5VsCQ

模型训练太慢？显存不够用？这个算法让你的GPU老树开新花

https://mp.weixin.qq.com/s/cYGMZuY7jSrjhUAXlDwD_w

Mixed Precision Training

https://zhuanlan.zhihu.com/p/441591808

混合精度训练原理

Flexpoint

Flexpoint是Nervana的作品。

论文：

《Flexpoint: An Adaptive Numerical Format for Efficient Training of Deep Neural Networks》

讲了Google的成功案例，这里来讲一个反面教材。

这实际上就是INT16的量化，用在inference上应该还是可以的，然而Nervana的目标还有training。

和bfloat16相比，它至少有如下问题：

• 格式转换比bfloat16复杂。

• Dynamic Range小，容易梯度消失，从而造成模型很难收敛。

从指数位宽来看，Flexpoint和float16相同，都是5位。然而由于Flexpoint是共享指数，因此它真正的Dynamic Range是不如float16的。

上图是模型训练过程中，相关值的典型范围。

float16已经被证明是不适合training的，更遑论Flexpoint了。

事实上，Intel内部已有人评价道：

Flexpoint16三个月converge不了一个网络，而BF16一天就可以converge三个。

• 指数保存在Host上，会造成反复通信的带宽问题。

总的来说，这个方案虽然精巧，但是由于没有对数据特点做充分分析，没有意识到Dynamic Range比底数精度更重要，从而导致了最终的失败。

目前，整个芯片行业，已经由过去芯片专家根据以往经验（比如摩尔定律），定义下一代产品的规格，逐渐过渡到根据实际应用定义芯片的阶段，即所谓的“软件定义硬件”。

BF16的成功经验表明，算法专家在AI芯片中的重要程度，甚至超过了IC专家。

需要注意的是Flexpoint的失败，主要在于Dynamic Range和底数的位宽取舍上。他的设计思路本身还是有可取之处的。采用同样思路的MSFP就获得了成功。

MSFP由微软提出，在微软Project Brainwave产品上得到了广泛的应用。