• Winograd
  • Winograd for CNN（续）
  • FFT与卷积
  • Strassen algorithm
  • NCHWc layout
  • 参考
• 模型压缩与加速
  • 课程
  • 复杂度分析
  • Network Pruning
  • 权值稀疏化实战

Winograd

Winograd for CNN（续）

https://github.com/andravin/wincnn

这个项目可以很方便的计算不同大小的核的Winograd的结果。这个项目中还有一个pdf文件作为上述论文的补充材料，详细的给出了各矩阵的计算方法。

---

介绍Winograd的论文里一般使用了如下表示法：

F(2x2,3x3)：

2x2: 一次性输出结果大小。注意这里的“一次性”的定语，对于大尺寸的输入tensor来说，这意味着需要重复进行若干次小计算，才能得到完整的输出结果。因此这里的size，更准确的说法是output tile size。

3x3: 卷积核大小

之所以采用这个方法，是因为改变这两者都会导致预处理的稀疏矩阵的变化。

---

论文：

《Efficient Sparse-Winograd Convolutional Neural Networks》

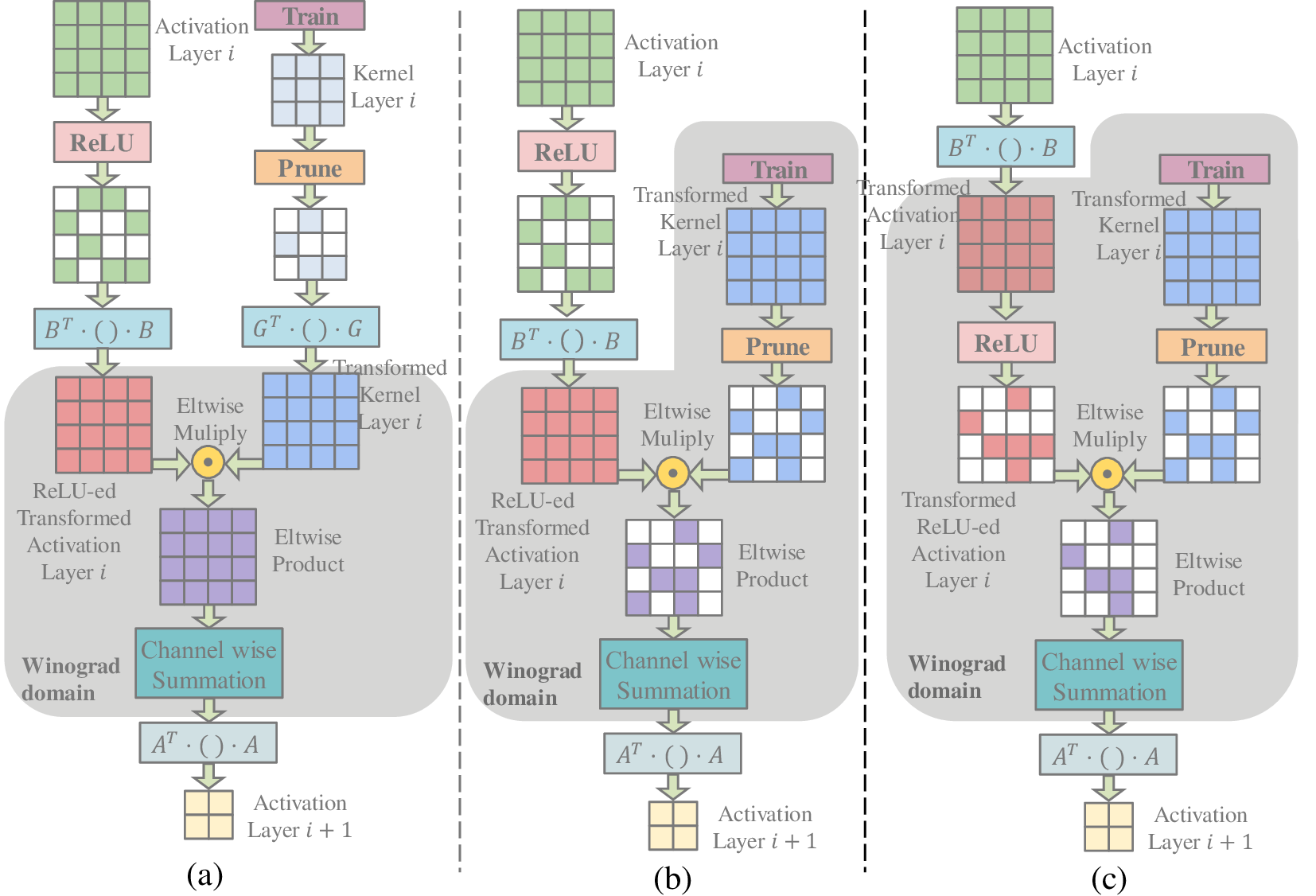
这篇论文（2018.2）讨论了如何在稀疏矩阵中应用Winograd算法。

论文：

《Sparse Winograd Convolutional neural networks on small-scale systolic arrays》

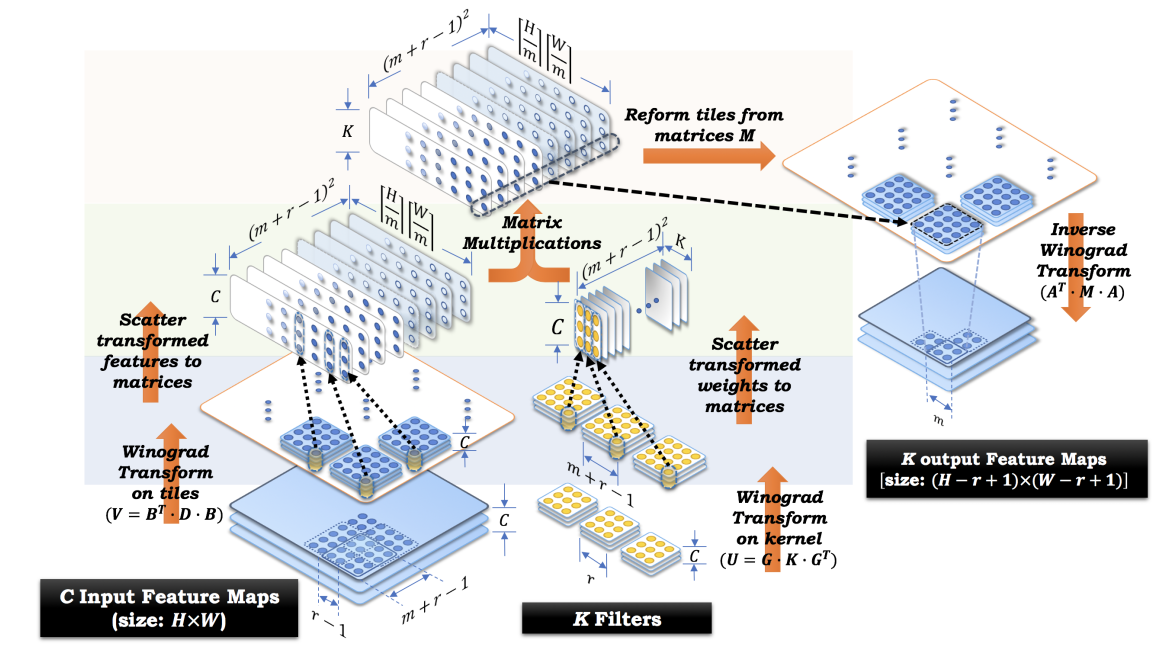
这篇论文（2018.10）讨论了如何在脉动阵列上实现Winograd算法，还讨论了3D卷积的计算方法。

参考：

http://shuokay.com/2018/02/21/winograd/

Winograd方法快速计算卷积

FFT与卷积

FFT是加速卷积运算的一种常用方法。但由于其原理，当卷积核小的时候，是没什么加速的，当核是3或者5时，速度有时更慢或者相当，而在CNN中卷积的核大多数比较小，FFT起到的加速作用很小，所以基本没人用。

此外，FFT是复数运算，如果没有特殊硬件，而用实数计算的话，还是比较费劲的。

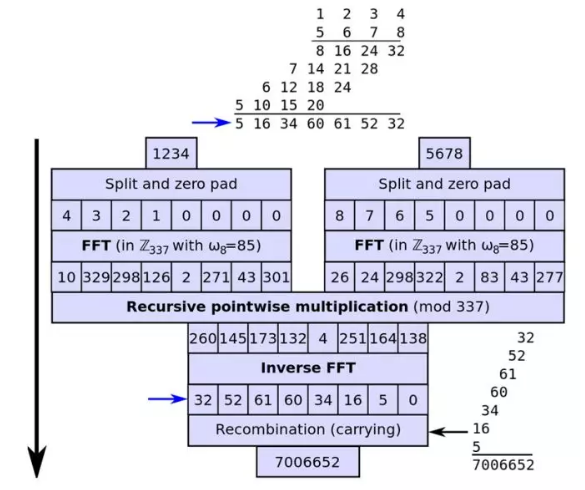
说句题外话，上图是FFT进行整数乘法的示例图。对于超大整数，2维的FFT是远远不够的。例如2019年2月，David Harvey和Van Der Hoeven就使用了1729维的FFT，计算了两个10亿位的超大整数的乘法。

参见：

http://www.cnblogs.com/jianyingzhou/p/4303578.html

convolution,fft, 加速

http://www.cnblogs.com/luoqingyu/p/5930181.html

数字信号处理–FFT与蝶形算法

http://blog.csdn.net/xxinliu/article/details/7438429

Cooley-Tukey算法 （蝶形算法）

https://www.zhihu.com/question/264307400

为什么很少人用FFT加速CNN卷积层的运算？

https://zhuanlan.zhihu.com/p/80297169

快速数论变换（NTT）及蝴蝶操作构造详解

https://mp.weixin.qq.com/s/fLGCBeSc8yQVsXHLSdogrA

柯尔莫哥洛夫惨遭打脸，没想到这个乘法难题被澳大利亚数学家解决了！

https://mp.weixin.qq.com/s/KxIDHg_2_meBGqACXJW94Q

PyTorch中的傅立叶卷积：通过FFT有效计算大核卷积的数学原理和代码实现

Strassen algorithm

上图展示的是Strassen algorithm的步骤，该算法也是在矩阵运算加速领域比较知名的算法。

然而，实际的情况要比理论计算复杂的多。

比如有的硬件支持加法/乘法的跳零（忽略对0的加法/乘法）操作，这时无论是Strassen还是Winograd都不会有太好的效果。

再者，Strassen不仅常数大，还需要补零到2^n，数值不稳定，甚至还对缓存不友好，所以Strassen实际上有可能完全打不过直接矩阵乘法。

NCHWc layout

常见的NCHW和NHWC两种layout，在硬件加速方面各有所长。因此，后来又出现了NCHWc这样的layout。

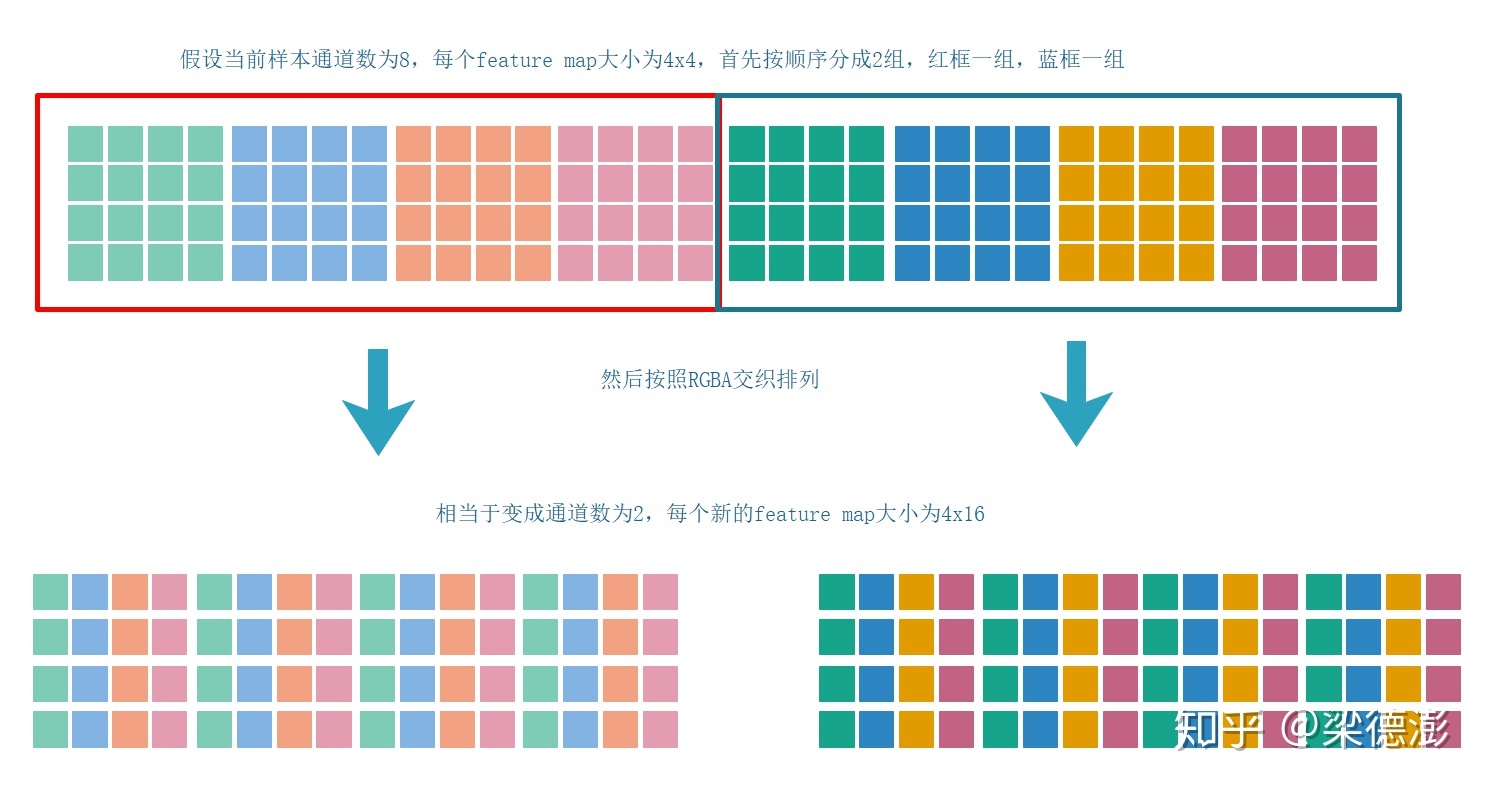
这种layout将C分成了两部分，局部的C放在了最后面，也就是NCHWc中的小写的c。这里c=4，因此又叫做NCHWc4。类似的还有NCHWc8。如果C不能被4整除的话，不足部分用0 pad即可。

c的大小主要由运算单元的block计算能力决定。比如Tensor core的尺寸，SIMD指令集单次运算的操作数个数等。

NCHWc对于CPU的SIMD指令集比较友好，因此被Intel广泛使用。

论文：

《Optimizing N-Dimensional, Winograd-Based Convolution for Manycore CPUs》

参考：

https://www.zhihu.com/question/337513515

Tensor中数据摆放顺序NC4HW4是什么意思，只知道NCHW格式，能解释以下NC4HW4格式吗？

https://mp.weixin.qq.com/s/1CToXRgyO0F8x0By31dneg

图解神秘的NC4HW4

参考

https://colfaxresearch.com/falcon-library/

FALCON Library: Fast Image Convolution in Neural Networks on Intel Architecture

https://www.intelnervana.com/winograd/

“Not so fast, FFT”: Winograd

https://www.encyclopediaofmath.org/index.php/Winograd_small_convolution_algorithm

Winograd small convolution algorithm

https://mp.weixin.qq.com/s/VcGwT0rKYQr13MQ_PRVmyg

每个AI程序员都应该知道的基础数论

https://mp.weixin.qq.com/s/jCPHXVI_utwnxaHqvW5nyA

商汤联合提出基于FPGA的快速Winograd算法：实现FPGA之上最优的CNN表现与能耗

https://www.leiphone.com/news/201804/SpmfJVa3al3uBDh2.html

斯坦福ICLR 2018录用论文：高效稀疏Winograd卷积神经网络

https://www.cnblogs.com/shine-lee/p/10906535.html

卷积神经网络中的Winograd快速卷积算法

https://mp.weixin.qq.com/s/RaW_WVKoLBk6jkoA6A3D-A

如何实现高速卷积？深度学习库使用了这些“黑魔法”

https://mp.weixin.qq.com/s/1JVPTv0ggD0IOEiZAa8mqA

深度神经网络卷积层计算加速与优化

https://zhuanlan.zhihu.com/p/80361782

卷积神经网络性能优化

https://mp.weixin.qq.com/s/Ji2PjZowifkIdGlHJPwEaw

解析卷积的高速计算中的细节，一步步代码带你飞

https://zhuanlan.zhihu.com/p/102351953

详解Winograd变换矩阵生成原理

模型压缩与加速

对于AI应用端而言，由于设备普遍没有模型训练端的性能那么给力，因此如何压缩模型，节省计算的时间和空间就成为一个重要的课题。

此外，对于一些较大的模型（如VGG），即使机器再给力，单位时间内能处理的图像数量，往往也无法达到实际应用的要求。这点在自动驾驶和视频处理领域显得尤为突出。

课程

https://cs217.github.io/

CS 217: Hardware Accelerators for Machine

https://mp.weixin.qq.com/s/RcEPWRxQXv6B4wqLHGyQHg

深度神经网络的高效处理:从算法到硬件架构，140页ppt

https://mp.weixin.qq.com/s/yp5gExPzpDiXaGk9oXEMVA

最新综述：模型压缩与加速

https://mp.weixin.qq.com/s/PraNMo4skR-VjEYIIqt1Cw

深度学习模型压缩与加速综述

https://mp.weixin.qq.com/s/Xqc4UgcfCUWYOeGhjNpidA

CNN模型压缩与加速算法综述

复杂度分析

https://zhuanlan.zhihu.com/p/31575074

卷积神经网络的复杂度分析

Network Pruning

首先是韩松的两篇论文：

《Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding》

《Learning both Weights and Connections for Efficient Neural Networks》

韩松，清华本科（2012）+Stanford博士（2017）。MIT AP（from 2018）。
个人主页：
https://stanford.edu/~songhan/

韩松也是SqueezeNet的二作。

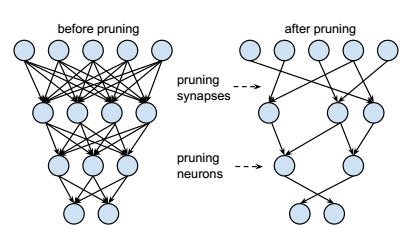
韩松论文的中心思想如上图所示。简单来说，就是去掉原有模型的一些不重要的参数、结点和层。

参数的选择，相对比较简单。参数的绝对值越接近零，它对结果的贡献就越小。这一点和稀疏矩阵有些类似。这种方法一般被称为Weight Pruning。

结点和层的选择，相对麻烦一些，需要通过算法得到不重要的层。删除结点一般被称为Filter Pruning，而删除层则相应的被称作Layer Pruning。

比如可以逐个将每一层50%的参数置零，查看模型性能。对性能影响不大的层就是不重要的。

Weight Pruning需要相关硬件支持跳零操作才能真正加速运算，而Filter/Layer Pruning则无需特殊硬件支持。

虽然这些参数、结点和层相对不重要，但是去掉之后，仍然会对准确度有所影响。这时可以对精简之后的模型，用训练样本进行re-train，通过残差对模型进行一定程度的修正，以提高准确度。

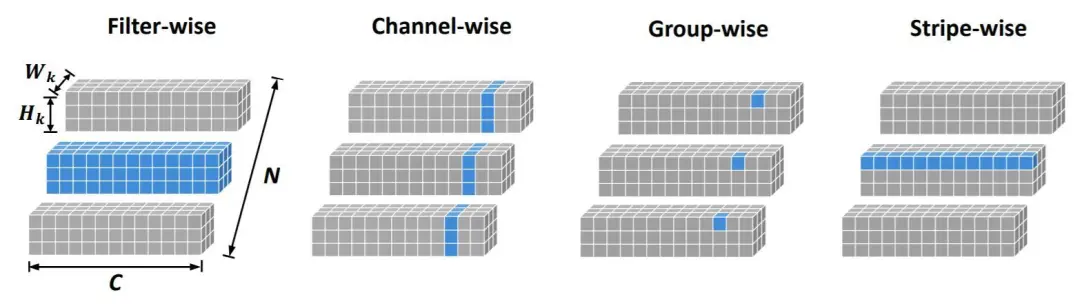
此外还有Stripe-Wise Pruning：

https://mp.weixin.qq.com/s/HohsD57cQtTR5SvuykEDuA

优图NeurIPS 2020论文，刷新滤波器剪枝的SOTA效果

还可以看看图森科技的论文：

https://www.zhihu.com/question/62068158

如何评价图森科技连发的三篇关于深度模型压缩的文章？

图森的思路比较有意思。其中的方法之一，是利用L1规则化会导致结果的稀疏化的特性，制造出一批接近0的参数。从而达到去除不重要的参数的目的。

除此之外，矩阵量化、Kronecker内积、霍夫曼编码、模型剪枝等也是常见的模型压缩方法。

---

彩票假说（ICLR2019会议的best paper）：随机初始化的密集神经网络包含一个初始化的子网，当经过隔离训练时，它可以匹配训练后最多相同迭代次数的原始网络的测试精度。

https://mp.weixin.qq.com/s/wOaCjSifZqkndaGbst1-aw

一文带你了解NeurlPS2020的模型剪枝研究

权值稀疏化实战

这里讲一下韩松论文提到的裁剪方法中，最简单的一种——“权值稀疏化“的工程实现细节。以darknet框架为例。

1.在src/parser.c中找到save_XXX_weights函数。判断权值是否接近0，如果是，则强制设为0。

2.使用修改后的weights进行re-train。训练好之后，重复第1、2步。

3.反复多次之后，进入最终prune阶段。修改src/network.c:update_network，令其不更新0权值。

re-train时的learning rate一般不宜太大。如果出现re-train的效果，还不如直接prune的好，则多半是learning rate设置的问题。

一般采用稀疏化率来描述权值的稀疏化程度。每层的稀疏化率可以相同，也可以不同。前者被称作Magnitude Pruner，而后者被称作Sensitivity Pruner。

权值稀疏化的设置也和网络结构有关。比如分类网络，由于输入图片是高维数据，而分类结果是低维数据，因此在稀疏化处理的时候，越靠近输出结果的Layer，其稀疏化程度就可以越高。而最初的几层，即使只加少量稀疏化，也会导致精度的大幅下降，这时往往就不做或者少做稀疏化处理了。

上述方法的问题在于，分类网络的计算量主要集中在最初几层，所以这种triangle prune mode对于压缩计算量的效果一般。

除了训练后的权值稀疏化之外，权值稀疏化训练也是一种方法。

论文：

《FLOPs as a Direct Optimization Objective for Learning Sparse Neural Networks》

这篇论文，将计算量也就是FLOPs作为Loss function设计的一部分，由于稀疏化的权值没有运算量，因此，采用这种Loss训练出的网络，天生就是稀疏化的。