• WFST（续）
  • FSM
  • FST
  • WFST
  • 相关的群论知识
  • Sum(Union)
  • Product(Concatenation)
  • Closure
  • Reversal
  • Inversion
  • Projection
  • Composition
  • Intersection
  • Difference
  • Connection
  • \(\epsilon\)-Removal
  • Determinization
  • Pushing
  • Minimization
  • Pruning
  • Other
  • HCLG
  • 参考

WFST（续）

FSM

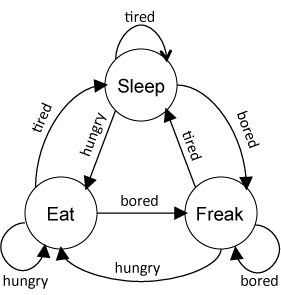
上图是finite-state machine（也叫finite-state automaton，FSA）的示意图。图中的Node表示State，顾名思义，FSM的State数量是有限的。图中的Edge表示Transition，Edge上的Label表示Input/Event。

FSM的含义是，在某一状态下，获得一个输入，从而产生一个状态转换。例如，上图中在Sleep状态下，如果输入是hungry的话，那么状态就会切换到Eat状态。当然了，输入也可以不改变状态，比如在Sleep状态下，输入是tired的时候。

FST

上图是finite-state transducers的示意图。FST和FSM的差别主要在Edge上的Label。FST收到Input的时候，不仅会发生状态改变，还会产生Output序列。因此，其Label的格式为input:output。

WFST

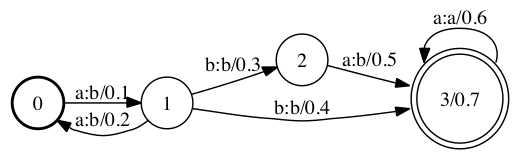
上图是WFST的示意图。顾名思义，Label上不仅有Input、Output，还有Weight信息，其格式为input:output/weight。

在有些图中会碰到\(\epsilon\). 这个符号在输入时表示不消耗任何输入，在输出位置表示不产生任何输出。

此外，还有格式为input/weight的FSM，一般被称为Weighted Finite-State Acceptors。

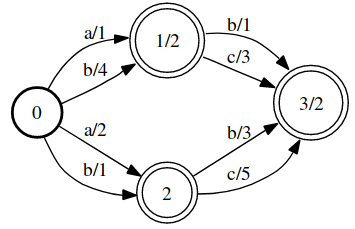
不仅Edge上的Label可以有权重，Node上的Label也可以有权重，如上图所示。没有权重的Label，其权重为1。

例如，上图中：

\[[A](ab)=1\times 1\times 2+2\times 3\times 2=14\]

相关的群论知识

WFST是基于半环代数理论的，在介绍半环之前我先简单的说一下群和半群。

群（Group）：G为非空集合，如果在G上定义的二元运算*，满足：

（1）封闭性（Closure）：对于任意\(a,b\in G\),有\(a*b\in G\);

（2）结合律（Associativity）：对于任意\(a,b,c\in G,(a*b)*c=a*(b*c)\);

（3）幺元（Identity）：存在幺元e，使得对于任意\(a\in G,e*a=a*e=a\);

（4）逆元：对于任意\(a\in G\),存在逆元\(a^{-1}*a=a*a^{-1}=e\)。

则称（G,*）为群。

半群（Semigroup）：仅满足封闭性和结合律群称为半群；如果还包含幺元，则成为幺元半群。

半环（semiring）：指具有两个二元运算\(+\)和\(\cdot\)的非空集合S，且满足：

（1）\((S,+),(S,\cdot)\)都是半群；

（2）\(\forall a,b,c\in S,(a+b)c = ac+bc, c(a+b) = ca+cb\)

半环的形式化表示如下：

\[(K, \bigoplus, \bigotimes，0， 1)\]

其中K是一个数集，\(\bigoplus, \bigotimes\)是两个二元操作，’0’和’1’是特定的（designated）零元素和幺元素（不一定是真正的数0和数1）。

常用的半环如下表所示：

Semiring	Set	\(\oplus\)	\(\otimes\)	0	1
Boolean	\(\{0,1\}\)	\(\lor\)	\(\land\)	0	1
Probability	\(R_+\)	\(+\)	\(\times\)	0	1
Log	\(R\cup\{-\infty，+\infty\}\)	\(\oplus_{log}\)	+	\(+\infty\)	0
Tropical	\(R\cup\{-\infty，+\infty\}\)	min	+	\(+\infty\)	0
String	\(\Sigma^*\cup\{\infty\}\)	\(\land\)	\(\cdot\)	\(\infty\)	\(\epsilon\)

在WFST中用的比较多的是log半环和tropical半环。前者对路径概率进行了对数运算，而后者在log半环的基础上，进行了viterbi approximation，也就是用若干路径的概率极值，作为当前概率值，这和动态规划中的viterbi算法是一致的。

接下来定义WFST上的二元运算：

一整条路径的权重\(w[\pi ]=w[e_1]\bigotimes \cdots \bigotimes w[e_k]\)。

多个有限路径集合的权重\(w[R]=\bigoplus_{\pi \in R} w[\pi]\)。

参考：

http://hongjiang.info/semigroup-and-monoid/

半群(semigroup)与幺半群(monoid)

https://mp.weixin.qq.com/s/wejmP4rrUCJ9uNcGqxXTfA

群论，Group Theory，135页pdf

Sum(Union)

介绍完WFST的定义，再来介绍一下定义在它之上的运算。

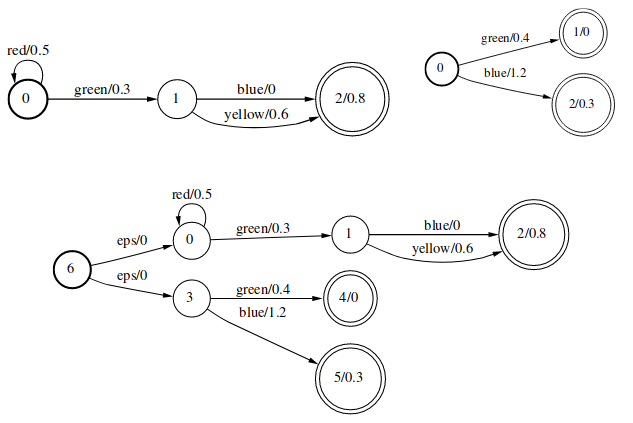
Sum运算的形式化描述为：

\[[T_1 \oplus T_2](x,y)=[T_1](x,y)\oplus [T_2](x,y)\]

Product(Concatenation)

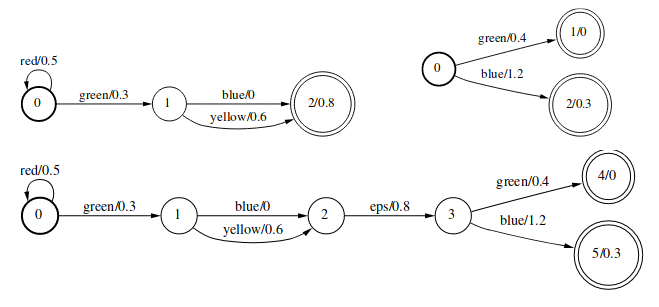
Product运算的形式化描述为：

\[[T_1 \otimes T_2](x,y)=\bigoplus_{x=x_1x_2,y=y_1y_2} [T_1](x_1,y_1)\otimes [T_2](x_2,y_2)\]

Closure

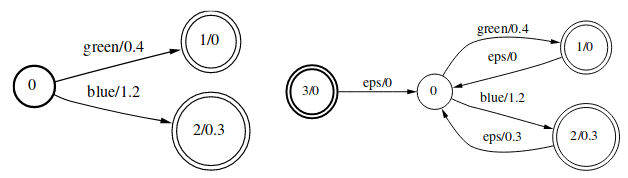
Closure运算的形式化描述为：

\[[T^*](x,y)=\bigoplus_{n=0}^{\infty}[T^n](x,y)\]

Reversal

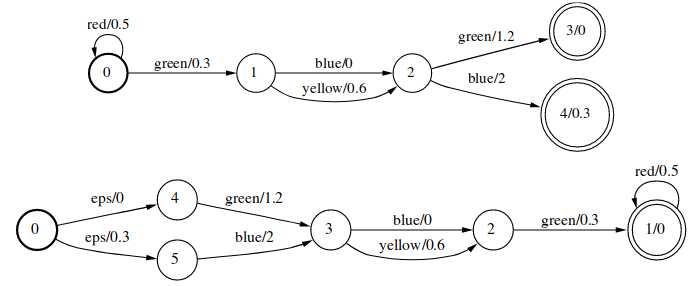
Reversal运算的形式化描述为：

\[[\widetilde{T}](x,y)=[T](\widetilde{x},\widetilde{y})\]

Inversion

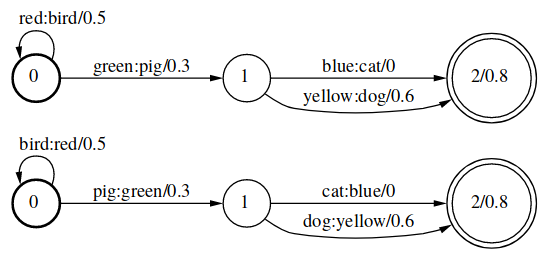
Inversion运算的形式化描述为：

\[[T^{-1}](x,y)=[T](y,x)\]

Projection

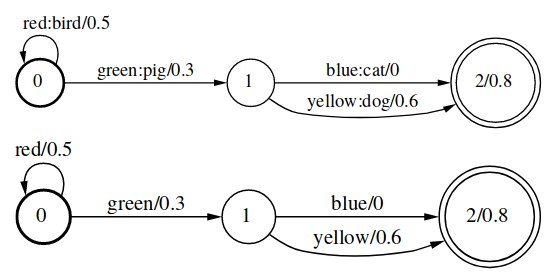
Projection运算的形式化描述为：

\[[\prod_1(T)](x)=\bigoplus_y[T](x,y)\]

Composition

Composition用来合并不同级别的转换器。用\(T=T_1\circ T_2\)表示这种操作。

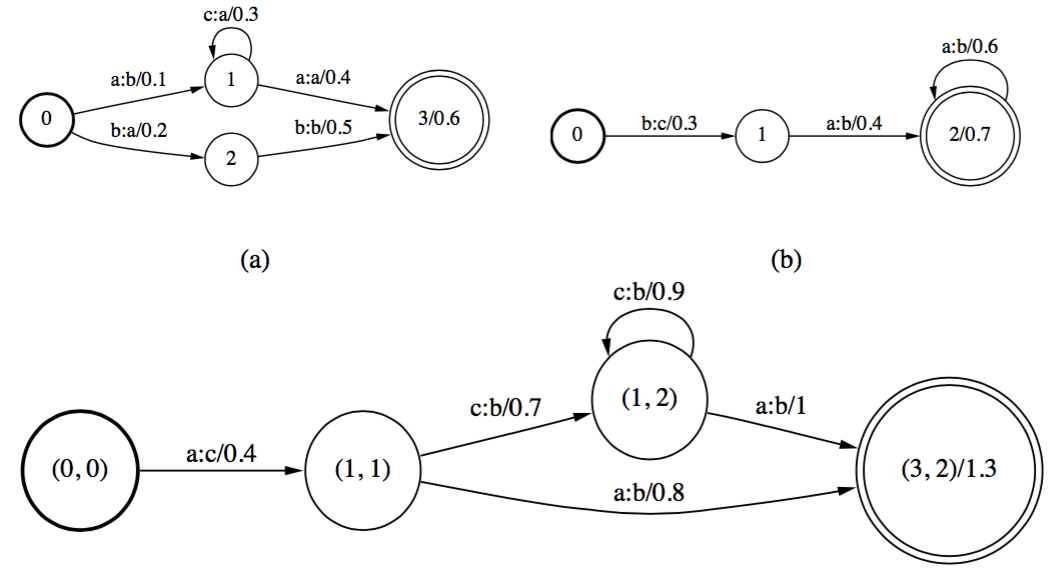
Composition运算的形式化描述为：

\[[T_1\circ T_2](x,y)=\bigoplus_z [T_1](x,z)\bigotimes [T_2](z,y)\]

通俗一些的说法就是：

（1）起始状态应该是\(T_1，T_2\)的起始状态

（2）结束状态是\(T_1，T_2\)的结束状态

（3）如果\(q_1\)到\(r_1\)的边\(t_1\)的输出等于\(q_2\)到\(r_2\)的边\(t_2\)的输入，那么\((q_1,q_2)\)和\((r_1,r_2)\)应该有一条边，如果是tripical半环，则该边权重是以上两边权重之和。

当\(T_1\)的输出包含\(\epsilon\)，\(T_2\)的输入包含\(\epsilon\)的时候，会导致产生大量多余的边，使得最终结果不正确。这时需要去除\(\epsilon\)-path。细节略。

Intersection

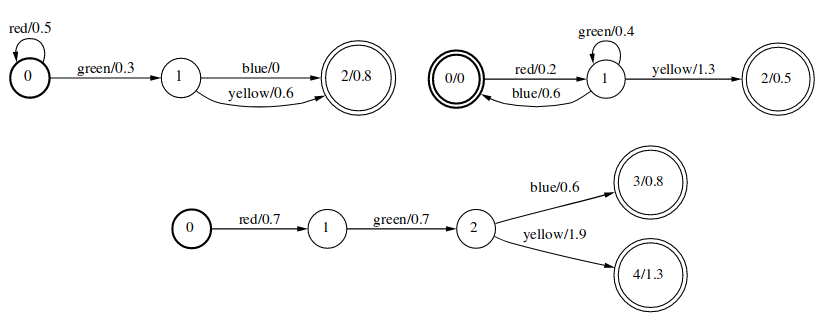
Intersection运算的形式化描述为：

\[[A_1\cap A_2](x)=[A_1](x)\otimes[A_2](x)\]

Intersection是求两个WFST的公共部分，并把相应的权重相加。

Difference

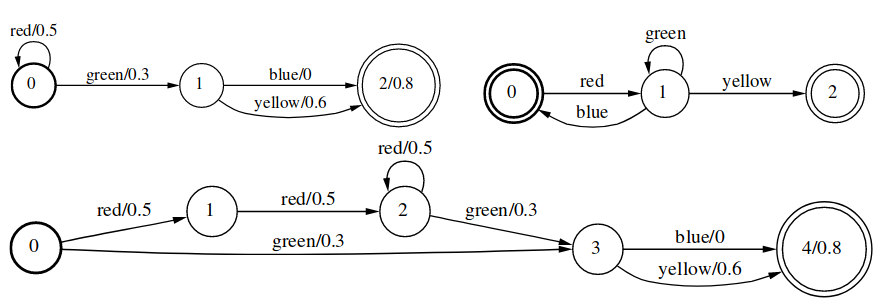
Difference运算的形式化描述为：

\[[A_1 - A_2](x)=[A_1\cap \overline{A_2}](x)\]

Difference大约是简单操作中最不好懂的了，我足足看了2个小时才看明白。

Difference的字面意思是：从A中去掉B。

比如上图中的A可以接受4个序列：ab,ad,cb,cd。但是ab,cd出现在B中，因此A-B就只有ad和cb了。可以看出，这里的B，其权重是无关紧要的，因此该操作要求B必须是无权重的FST。

Connection

下面的几个运算属于图优化的范畴，因此没有简单的形式化描述，而只有算法流程。但限于篇幅，这里只讲运算的含义，而不讲具体的算法流程。

既然是优化，则运算前后的FST必然是等价的。

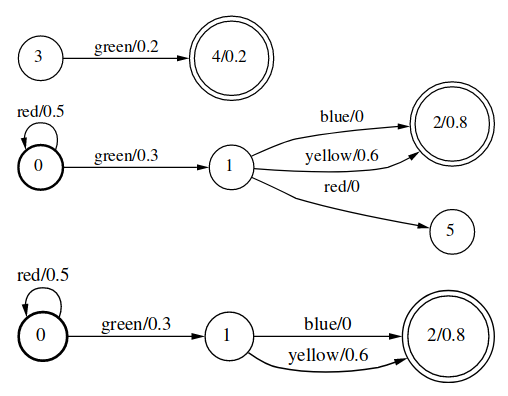
Connection运算用于计算FST的连通性。上图中的状态3，4和初始状态0之间没有连通，所以应该去掉。状态5没有路径到达终止状态2，所以也应该去掉。

\(\epsilon\)-Removal

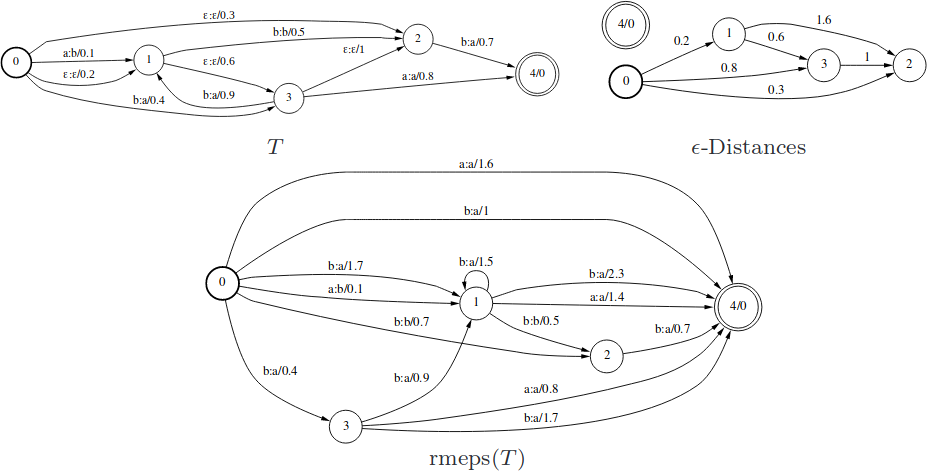
\(\epsilon\)-Removal运算用于去除FST中的\(\epsilon\)-transitions。

这里分为两步。

Step1：计算\(\epsilon\)-closures。closures中两个State的距离被称作\(\epsilon\)-Distances，这里不妨用\(ED(A\to B)\)来表示。

例如上图中：

\[ED(0\to 3)=ED(0\to 1)+ED(1\to 3)=\epsilon:\epsilon/0.2+\epsilon:\epsilon/0.6=\epsilon:\epsilon/0.8\]

Step2：去除\(\epsilon\)-transitions。

这里以0->4之间的a:a/1.6为例介绍一下计算方法。首先，0->4之间并没有直接的a:a连线，但是3->4有a:a连线。因此：

\[a:a/0.8+ED(0\to 3)=a:a/0.8+\epsilon:\epsilon/0.8=a:a/1.6\]

Determinization

Determinization：所有状态在接受某个输入后只有一条输出边，而且不包含\(\epsilon\)。

这个操作的根本前提：两个自动机或者转换器是否相等，不需要每条边，每个权重都相等。只需要对于任何一个输入序列，其输出及权重相同，而不用在意权重的分布是否相同。

一般使用\(\otimes\)来计算分支内的权重。使用\(\oplus\)来处理分支间最终输出的权重。

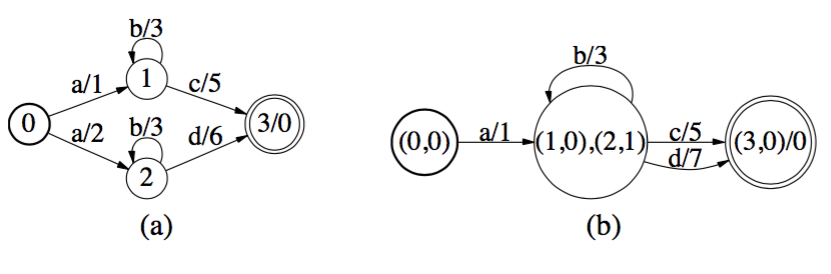
Determinization之后的FST采用(原始状态号,剩余权重)的方式表示Node。例如上图中，从(0,0)到(1,0)(2,1)的边a/1上消耗权重1，原图状态1，状态2剩余权重分别是0和1，所以用(1,0)(2,1)表示。 在输出到下一个状态时候，将剩余权重加上。比如原图中d/6,这里变成d/7。

Pushing

Pushing包括Weight Pushing和Label Pushing两种情况。

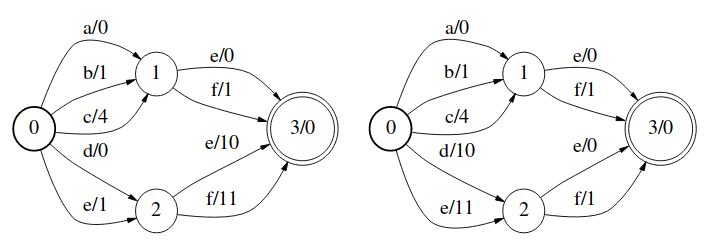
上图是Weight Pushing的例子。如果WFST不在乎权重的分布，而只在乎最终权重的大小的话，则可以将权重前推（Pushing），以利于最小化。

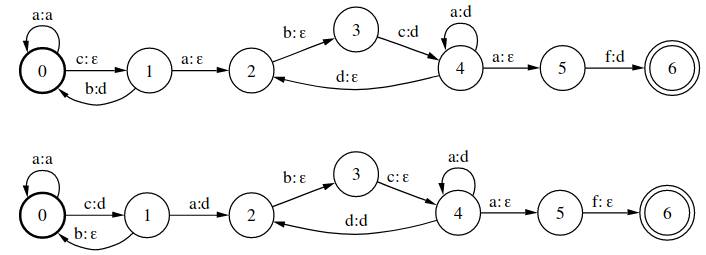
上图是Label Pushing的例子，将非\(\epsilon\)的label前推。

Kaldi中没有使用weight pushing。

Minimization

最小化的目的是减少原图中的状态数，以及转移边数。从而减少存储空间和计算时间。

最小化一般是消除相同结点。常用算法与DFA的最小化算法类似。

Pruning

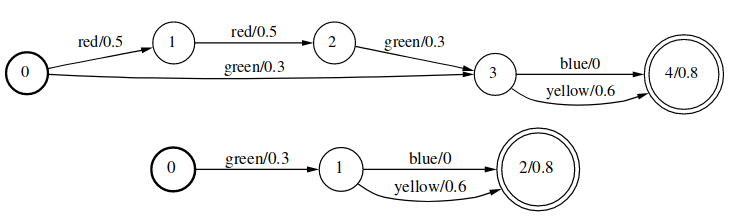
Pruning的目的是去除大于最短路径的\(\otimes\)分支。

Other

除了这些常用操作之外，还有add-self-loops和remove-disambiguation-symbols等操作。这里不再赘述。

HCLG

介绍完WFST的基本运算，这里来介绍一下WFST在语音识别上的应用——HCLG。

上图中，Language Model又名Grammar Model，Phonemic Model又名Lexicon Model，故名HCLG。

这个流程的形式化描述为：

\[H\circ C\circ L\circ G\]

直接使用这个WFST的状态空间较大，搜索效率比较低，Mohri因此提出了一个简化方案：

\[N = \pi_{\epsilon} (min(det(\tilde{H} \circ det(\tilde{C} \circ det(\tilde{L} \circ G)))))\]

参考

https://www.microsoft.com/en-us/research/wp-content/uploads/2016/11/ParallelizingWFSTSpeechDecoders.ICASSP2016.pdf

《parallelizing WFST speech decoders》

http://www.cs.nyu.edu/~mohri/pub/csl01.pdf

《Weighted Finite-State Transducers in Speech Recognition》

https://blog.csdn.net/l_b_yuan/article/category/6132477

这个专栏包含了4篇WFST的blog

http://djt.qq.com/article/view/507

定制你的语音识别-并行语音识别解码空间

https://blog.csdn.net/lucky_ricky/article/details/77511543

Kaldi WFST 构图 学习