speech » 语音识别(五)——Cepstrum Analysis, Mel-Frequency Analysis
2018-06-06 :: 5503 WordsSpectrogram(续)
Hann window
Hann window虽然是以Julius Ferdinand von Hann的名字命名,但却是Blackman和Tukey的作品。他们和同一实验室的Claude E. Shannon, Hendrik Wade Bode,合称为Information Age的四大先锋。
Julius Ferdinand von Hann,1839~1921,奥地利气象学家。现代气象学之父。
Ralph Beebe Blackman,1904~1990,美国数学家。长期供职于AT&T Bell Laboratories。二战时,参与了防空火炮控制系统的平滑研究。
\[w(n) = \sum_{k = 0}^{K} (-1)^k a_k\; \cos\left( \frac{2 \pi k n}{N-1} \right),\quad 0\le n \le N-1\]John Wilder Tukey,1915~2000,美国数学家。Princeton University博士,长期供职于AT&T Bell Laboratories。英国皇家学会会员。Cooley–Tukey FFT算法发明者。
上式是Cosine-sum windows的计算公式,令K=1,则:
\[w(n) = a_0 - \underbrace{(1-a_0)}_{a_1}\cdot \cos\left( \tfrac{2 \pi n}{N - 1} \right),\quad 0\le n \le N-1\]这类Window function有好几个特例:
Hann window:
\[w(n) = 0.5\; \left[1 - \cos \left ( \frac{2 \pi n}{N-1} \right) \right] = \sin^2 \left ( \frac{\pi n}{N-1} \right)\]Hamming window:
\[w(n) = 0.54 - 0.46\cdot \cos\left( \tfrac{2 \pi n}{N - 1}\right)\]Richard Wesley Hamming,1915~1998,美国数学家。University of Chicago本科(1937)+University of Nebraska硕士(1939)+UIUC博士(1942)。参与曼哈顿计划,后长期供职于Bell Lab。通信和计算机工程领域的宗师级人物,美国工程院院士,图灵奖得主(1968)。Hamming code 、Hamming distance等都是他的贡献。
STFT
\[\mathbf{STFT}\{x(t)\}(\tau,\omega) \equiv X(\tau, \omega) = \int_{-\infty}^{\infty} x(t) w(t-\tau) e^{-j \omega t} \, dt\]上式是STFT(Short-time Fourier transform)的定义。和FT相比,STFT将FT中的被积函数\(x(t)\),换成了\(x(t) w(t-\tau)\)。其中,w(t)是窗函数(Window function),因此STFT又叫做加窗傅立叶变换。
参考:
https://mp.weixin.qq.com/s/TsO-tope0m4sHfVmZ0_Hog
STFT极简版
Spectrogram
DTW是一种时域方法,作为信号处理自然少不了频域方法。这里我们先来了解一个叫声谱图的东西。
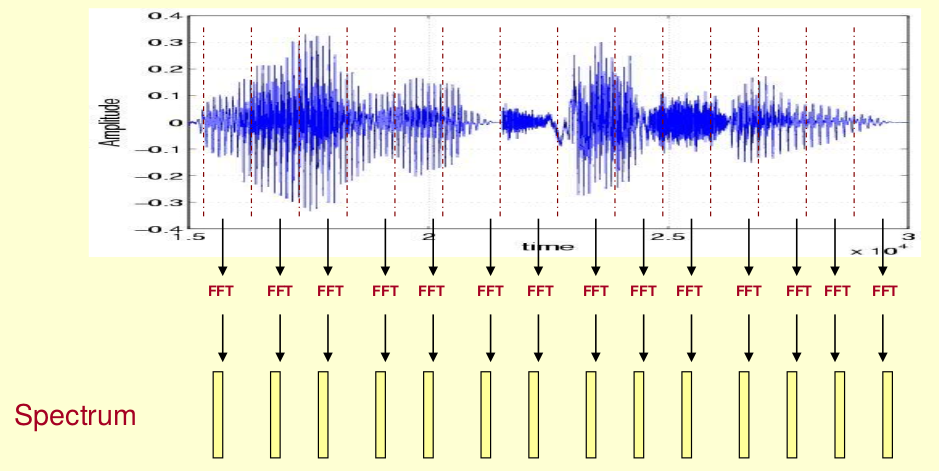
这段语音被分为很多帧,每帧语音都对应于一个频谱(通过短时FFT计算),频谱表示频率与能量的关系。在实际使用中,频谱图有三种,即线性振幅谱、对数振幅谱、自功率谱(对数振幅谱中各谱线的振幅都作了对数计算,所以其纵坐标的单位是dB(分贝)。这个变换的目的是使那些振幅较低的成分相对高振幅成分得以拉高,以便观察掩盖在低幅噪声中的周期信号)。
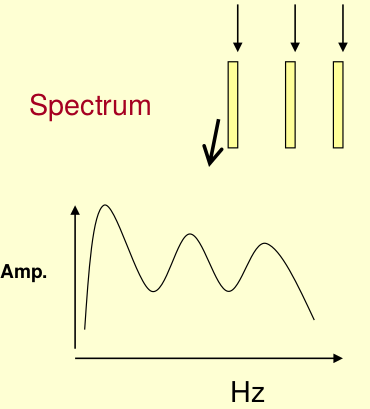
我们先将其中一帧语音的频谱通过坐标表示出来。
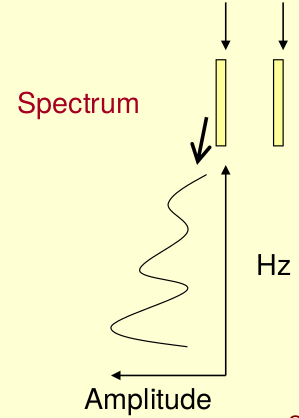
再将左边的频谱旋转90度。
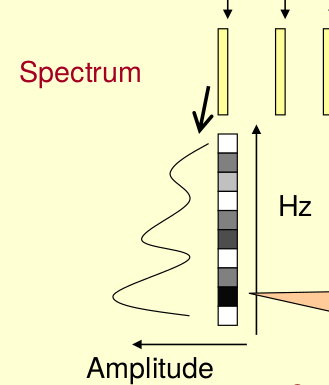
然后把这些幅度映射到一个灰度级表示的直方图。0表示白色,255表示黑色。幅度值越大,相应的区域越黑。
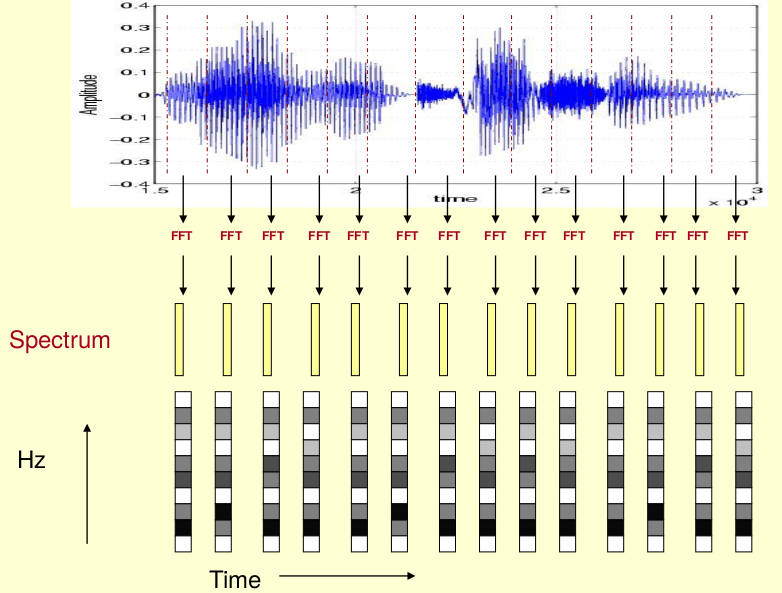
这样我们会得到一个随着时间变化的频谱图,这个就是描述语音信号的spectrogram声谱图。
Cepstrum Analysis
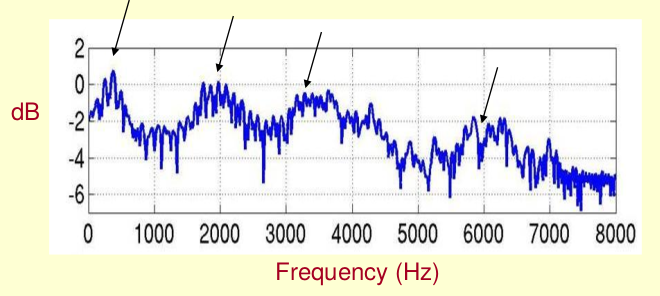
上图是一个语音的频谱图。峰值就表示语音的主要频率成分,我们把这些峰值称为共振峰(formants),而共振峰就是携带了声音的辨识属性(就是个人身份证一样)。所以它特别重要。用它就可以识别不同的声音。
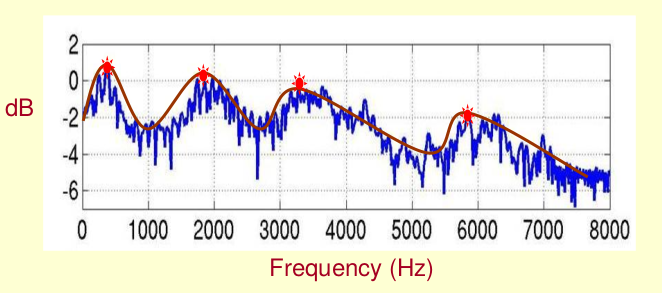
既然它那么重要,那我们就是需要把它提取出来!我们要提取的不仅仅是共振峰的位置,还得提取它们转变的过程。所以我们提取的是频谱的包络(Spectral Envelope)。这包络就是一条连接这些共振峰点的平滑曲线。
原始的频谱由两部分组成:包络和频谱的细节。这里用到的是对数频谱,所以单位是dB。
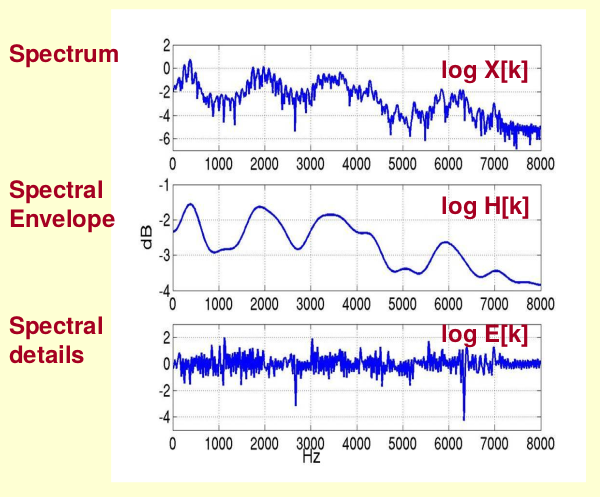
怎么把他们分离开呢?也就是,怎么在给定\(\log X[k]\)的基础上,求得\(\log H[k]\)和\(\log E[k]\)以满足\(\log X[k] = \log H[k] + \log E[k]\)呢?
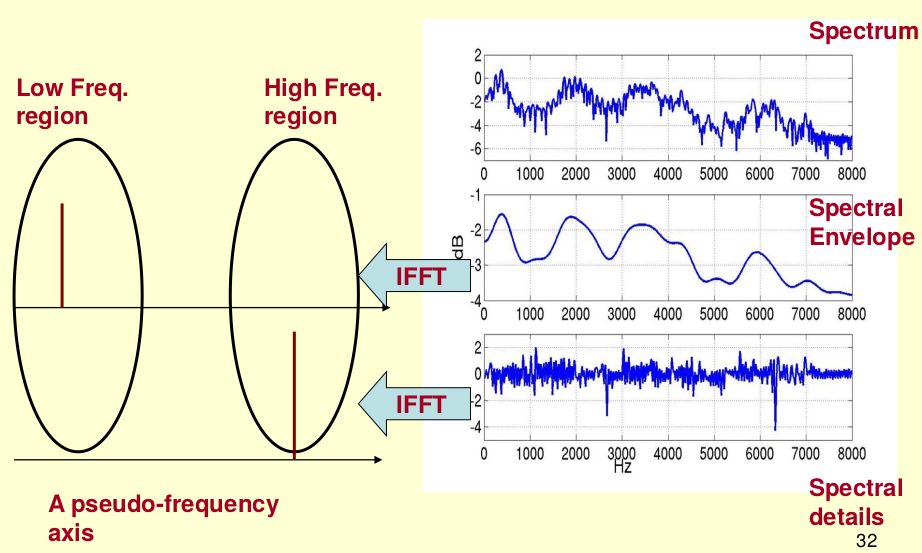
为了达到这个目标,我们需要Play a Mathematical Trick。这个Trick是什么呢?就是对频谱做FFT。
这里,我们对Fourier transform做一个简单的回顾。
设h(t)是一个时域函数,而H(f)是一个频域函数,则Fourier transform为:
\[H(f)=\int_{-\infty}^\infty h(t)e^{2\pi i ft}\mathrm{d}t\]inverse Fourier transformation为:
\[h(t)=\int_{-\infty}^\infty H(f)e^{-2\pi i ft}\mathrm{d}f\]因此,对频谱做FT,也被叫做inverse FT,简称IFT。
从上式还可以看出,FT和IFT的公式非常类似,因此从编程角度,一个FT函数既可以做FT,也可以稍作修改后,做IFT运算。因此在不强调目的性的情况下,IFT也可以直接称为FT。比如,MFCC特征最后的IDFT变换,实际上是DCT变换。
传统的IFFT的结果是一个时域函数,然而这里是对log frequency domain做IFFT,因此,它的值域只能被称作pseudo-frequency domain。
从上图可以看出,Spectral Envelope主要是低频成分,而Spectral details主要是高频成分。
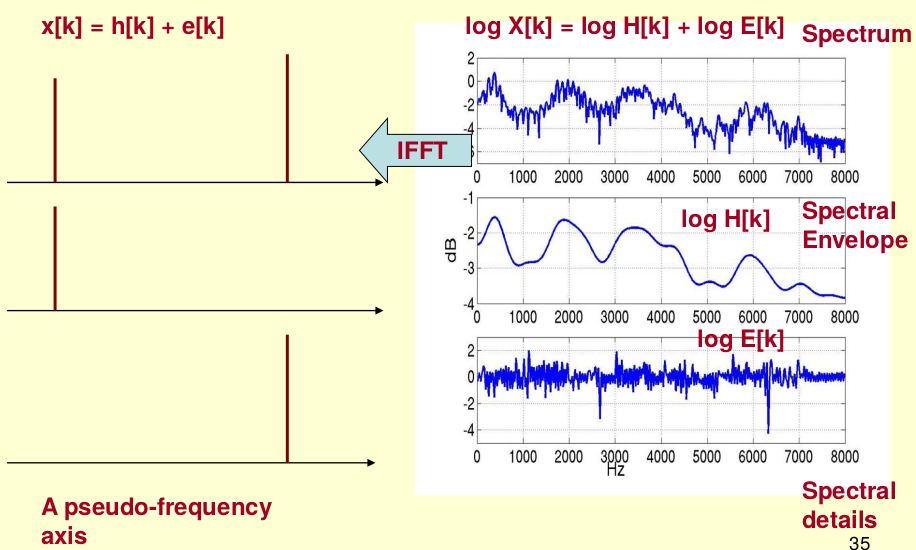
显然,如果把Spectral Envelope和Spectral details叠加起来就是原来的频谱信号了。
换句话说,我们知道了\(\log X[k]\),就可以求出\(x[k]\),经过低通滤波就可以得到\(h[k]\)。
这里的\(x[k]\)被称作倒谱Cepstrum(这个是一个新造出来的词,把spectrum的前面四个字母顺序倒过来就是倒谱的单词了)。
而我们所关心的\(h[k]\)就是倒谱的低频部分,它在语音识别中被广泛用于描述特征。
参考:
https://www.zhihu.com/answer/790986702
怎样让安卓手机均匀连续地循环播放某一频率段的声波?
Mel-Frequency Analysis
Mel scale
Mel scale是Stevens、Volkmann和Newman于1937年发明的一种主观音阶标准。
Stanley Smith Stevens,1906~1973,Harvard University心理学教授。
John E. Volkmann,1905~1980,Radio Corporation of America研究员。
Edwin B. Newman,1908~1989,Harvard University心理学教授。
声音作为一种波动,一般以Hz作为频率差异的客观标准,然而相同频率差的两组声音,在人耳听来,其频率差(也就是所谓的音阶)实际上是不同的。因此,Stevens等人采取实验的方法,确定了人耳的主观音阶标准。
该标准以Mel作为单位,规定1000Hz的声音所对应的音阶为1000Mel。
Mel scale从严格的定义上并没有一个简单的公式来表示。但一般采用如下公式进行转换:
\[m = 2595 \log_{10}\left(1 + \frac{f}{700}\right)\]从中可以看出,人耳对于高频声音的分辨率实际上是不如低频声音的。
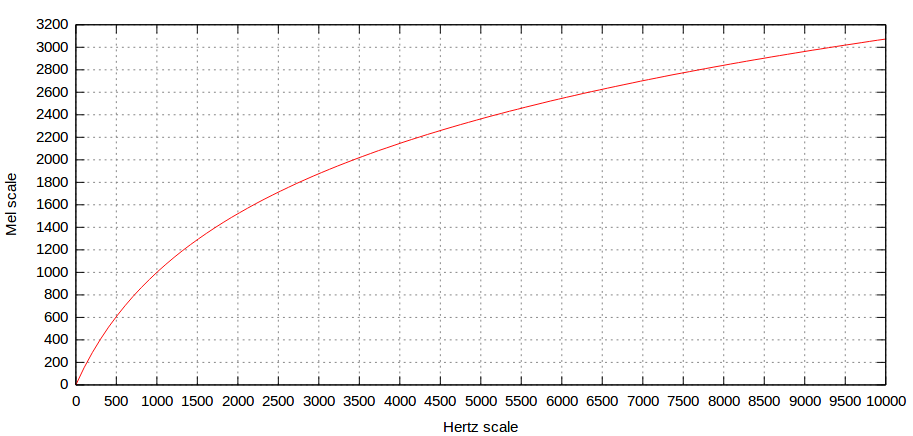
Mel是melody的别称,有的blog上说Mel是个人,他发明了MFCC,这纯粹是胡说八道。
MFCC
Mel-frequency Cepstral Coefficients是由Paul Mermelstein提出的一种音频特征。
Paul G. Mermelstein,明尼苏达大学神经科学教授。
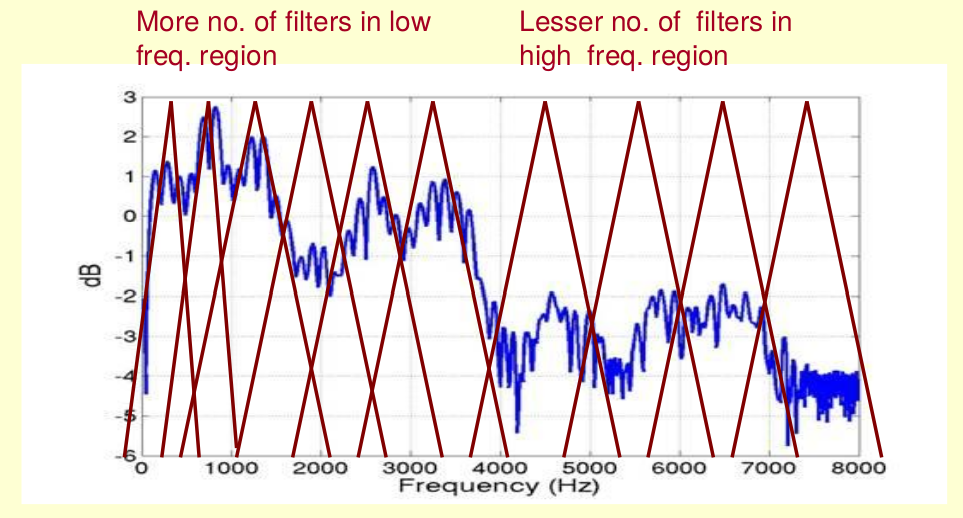
由之前对Mel scale的介绍可知:人耳对于高频声音的分辨率实际上是不如低频声音的。
因此,我们可以使用一组Triangular window对声音进行滤波(如上图所示)。这里的Triangular window不是均匀分布的,而是低频部分更密集一些。
这些Triangular window被称作Mel-Filters。被Mel-Filters过滤之后的Spectrum,被称作Mel-Spectrum。
对Mel-Spectrum执行Cepstrum Analysis,就得到了Mel-Frequency Cepstral Coefficients,也就是MFCC。
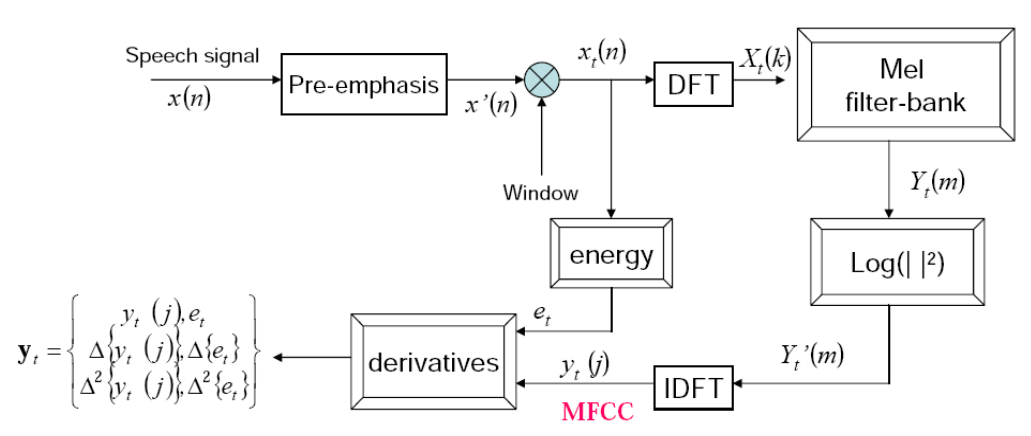
上图是MFCC的计算流程。
除了MFCC之外,delta MFCC和double-delta MFCC也是常用的特征。他们的计算过程如下所示:
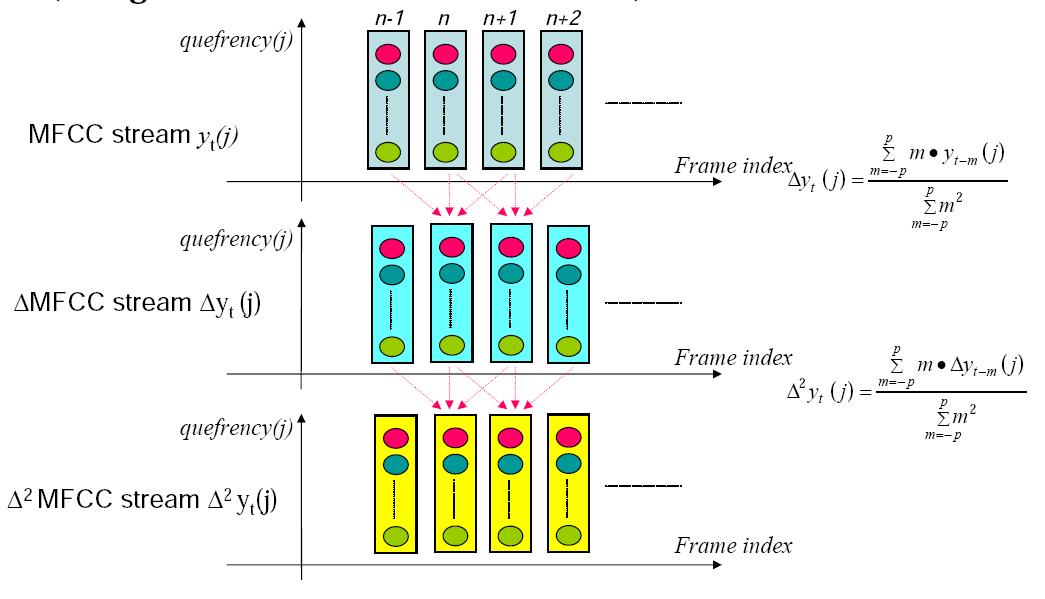
可见,delta MFCC和double-delta MFCC,实际上就是MFCC的一阶差分和二阶差分。
在实际中使用的语音特征,往往是各种特征的组合。比如,常用的39维MFCC特征,其组成如下:
12 MFCC feature
1 energy feature
12 delta MFCC features
12 double-delta MFCC features
1 delta energy feature
1 double-delta energy feature
其他的语音特征还有:
- Amplitude Envelope
- Root-Mean-Square Energy
- Zero Crossing Rate
参考:
https://mp.weixin.qq.com/s/KFBINcap3dIOVPjpBEbj6w
浅谈MFCC/HMM/GMM/EM/LM
https://mp.weixin.qq.com/s/LI-jGrG19IZH9QY9cjqQ3A
音频时域特征的提取
计算能量谱
energy的计算比较简单,无论是如上图的时域能量统计,还是在DFT之后进行频域能量统计都是可以的。参见《数学狂想曲(一)》。
需要注意的是,频域能量包含了实部能量+虚部能量。
Discrete Cosine Transform
离散傅立叶变换需要进行复数运算,尽管有FFT可以提高运算速度,但在图像编码、特别是在实时处理中非常不便。离散傅立叶变换在实际的图像通信系统中很少使用,但它具有理论的指导意义。
根据离散傅立叶变换的性质,实偶函数的傅立叶变换只含实的余弦项,因此构造了一种实数域的变换——离散余弦变换(DCT)。
通过研究发现,DCT除了具有一般的正交变换性质外,其变换阵的基向量很近似于Toeplitz矩阵的特征向量,后者体现了人类的语言、图像信号的相关特性。因此,在对语音、图像信号变换的确定的变换矩阵正交变换中,DCT变换被认为是一种准最佳变换。
相对应的还有IDCT。
DCT还有一个特点是,对于一般的语音信号,这一步的结果的前几个系数特别大,后面的系数比较小,可以忽略。比如Mel-Filters一般取40个三角形,所以DCT的结果也是40个点;实际中,一般仅保留前12~20个,这就进一步压缩了数据。
类似的,还有Discrete Sine Transform,它和DCT的区别在于:DST用于实奇对称数据,而DCT用于实偶对称数据。这里的对称指的是采样对称,而非物理数值上的对称。
除此之外,针对人耳的听觉特性,还有Constant-Q transform。它与STFT的公式基本相同,差别在于后者的filter的中心频点间隔均匀,而前者的间隔越往高频越稀疏:
\[\delta f_k = 2^{1/n} \cdot \delta f_{k-1} = \left( 2^{1/n} \right)^k \cdot \delta f_\text{min}\]上式中的\(f_k\)即为filter的中心频点。

您的打赏,是对我的鼓励
