• 声学模型
• 解码器技术
• 人类声音
• 建模单元
• DTW
• Spectrogram
  • Window function

声学模型

声学模型主要有两个问题，分别是特征向量序列的可变长和音频信号的丰富变化性。

可变长特征向量序列问题在学术上通常有动态时间规划（Dynamic Time Warping, DTW）和隐马尔科夫模型（Hidden Markov Model, HMM）方法来解决。

音频信号的丰富变化性是由说话人的各种复杂特性或者说话风格与语速、环境噪声、信道干扰、方言差异等因素引起的。声学模型需要足够的鲁棒性来处理以上的情况。

在过去，主流的语音识别系统通常使用梅尔倒谱系数（Mel-Frequency Cepstral Coefficient, MFCC）或者线性感知预测（Perceptual Linear Prediction, PLP）作为特征，使用混合高斯模型-隐马尔科夫模型（GMM-HMM）作为声学模型。

在近些年，区分性模型，比如深度神经网络（Deep Neural Network, DNN）在对声学特征建模上表现出更好的效果。基于深度神经网络的声学模型，比如上下文相关的深度神经网络-隐马尔科夫模型（CD-DNN-HMM）在语音识别领域已经大幅度超越了过去的GMM-HMM模型。

参考：

https://zhuanlan.zhihu.com/p/23567981

声学模型

解码器技术

解码器模块主要完成的工作包括：给定输入特征序列\(x_1^T\)的情况下，在由声学模型、声学上下文、发音词典和语言模型等四种知识源组成的搜索空间（Search Space）中，通过维特比（Viterbi）搜索，寻找最佳词串\([w_1^N]^{opt}=[w_1,\dots,w_N]_{opt}\)，使得满足：

\[[w_1^N]^{opt}=\mathop{\arg\max}_{w_1^N,N}p(w_1^N\mid x_1^T)\]

在解码过程中，各种解码器的具体实现可以是不同的。按搜索空间的构成方式来分，有动态编译和静态编译两种方式。

静态编译，是把所有知识源统一编译在一个状态网络中，在解码过程中，根据节点间的转移权重获得概率信息。由AT&T提出的Weighted Finite State Transducer（WFST）方法是一种有效编译搜索空间并消除冗余信息的方法。

动态编译，预先将发音词典编译成状态网络构成搜索空间，其他知识源在解码过程中根据活跃路径上携带的历史信息动态集成。

参考：

https://zhuanlan.zhihu.com/p/23648888

语音识别之解码器技术简介

人类声音

成年男性：80-140 Hz

成年女性：130-220 Hz

儿童：180-320 Hz

从信号处理的角度，人类声音的处理方式和普通的雷达信号处理并无本质差异，主要的区别在于：雷达信号经过了载波调制，而人类声音则没有这个步骤。

参考：

https://wenku.baidu.com/view/6123ba2f0066f5335a8121fe.html

人声频率范围及各频段音色效果

建模单元

建模单元是指声音建模的最小单元。从细到粗，一般有state、phoneme、character三级。

描述一种语言的基本单位被称为音素phoneme，例如BRYAN这个词就可以看做是由B, R, AY, AX, N五个音素构成的。这种模式也叫做单音素monophone模式。

然而语音没有图像识别那么简单，因为我们在说话的时候很多发音都是连在一起的，很难区分，所以一般用左中右三个HMM state来描述一个音素，也就是说BRYAN这个词中的R音素就变成了用B-R, R, R-AY三个HMM state来表示。这种模式又被称作三音素triphone模式。

character显然是个最粗的划分，尽管英语是表音文字，然而一个字母有多个发音，仍然是个普遍现象。

在GMM-HMM时代，人们倾向于细粒度建模，因为模型越细，效果越好。但DL时代，人们更倾向于粗粒度建模，因为这样做，可以加快语音识别的解码速度，从而可以使用更深、更复杂的神经网络建模声学模型。

DTW

Dynamic Time Warping是Vintsiuk于1968年提出的算法。

Taras Klymovych Vintsiuk，1939～2012，乌克兰科学家，毕业于Kyiv Polytechnic Institute。模式识别专家，语音识别领域的奠基人之一。

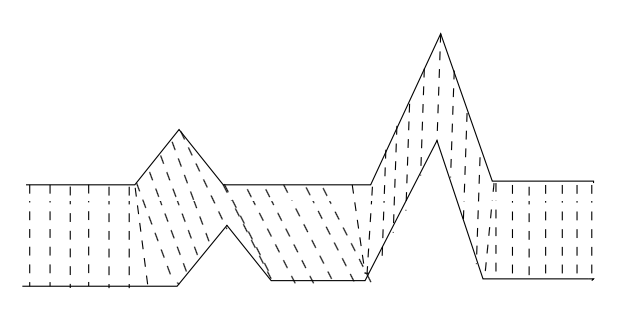
图1

如上图所示，因为语音信号具有相当大的随机性，即使同一个人在不同时刻发同一个音，也不可能具有完全的时间长度。而且同一个单词内的不同音素的发音速度也不同，比如有的人会把“A”这个音拖得很长，或者把“i”发的很短。在这些复杂情况下，使用传统的欧几里得距离，无法有效地求得两个时间序列之间的距离（或者相似性）。

回到上面的图。如果我们将两个序列中相关联的点，用上图中的虚线连接的话，就会发现这两个序列实际上是很相似的。

那么如何用数学的方式描述上述DTW算法的思想呢？

假设现在有一个标准的参考模板R，是一个M维的向量，即\(R=\{R(1),R(2)，\dots，R(M)\}\)，每个分量可以是一个数或者是一个更小的向量。现在有一个才测试的模板T，是一个N维向量，即\(T=\{T(1),T(2)，\dots，T(N)\}\)同样每个分量可以是一个数或者是一个更小的向量，注意M不一定等于N，但是每个分量的维数应该相同。

然后，将两个序列二维展开得到下图：

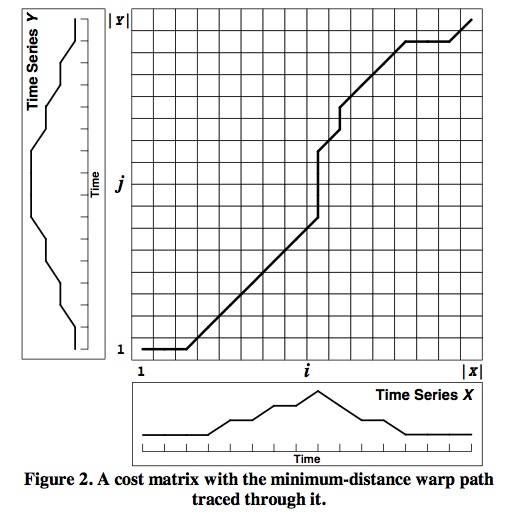
这样，两个序列中点与点之间的关联关系，就可以用这个二维矩阵W来表述。比如，可以用W(i,j)表示第1个序列中的第i个点和第2个序列中的第j个点相对应。所有这样的W(i,j)最终构成了上图中的曲线。这条曲线也被称作归整路径（Warp Path）。

显然，这个归整路径不是随意选择的，它需要满足以下几个约束：

1）边界条件：\(w_1=(1,1)\)和\(w_k=(m,n)\)。任何一种语音的发音快慢都有可能变化，但是其各部分的先后次序不可能改变，因此所选的路径必定是从左下角出发，在右上角结束。

2）连续性：如果\(w_{k-1}= (a’, b’)\)，那么对于路径的下一个点\(w_k=(a, b)\)需要满足\((a-a’) \le 1\)和\((b-b’) \le 1\)。也就是不可能跨过某个点去匹配，只能和自己相邻的点对齐。这样可以保证R和T中的每个坐标都在W中出现。

3）单调性：如果\(w_{k-1}= (a’, b’)\)，那么对于路径的下一个点\(w_k=(a, b)\)需要满足\(0\le (a-a’)\)和\(0\le (b-b’)\)。这限制W上面的点必须是随着时间单调进行的。以保证图1中的虚线不会相交。

结合连续性和单调性约束，每一个格点的路径就只有三个方向了。例如如果路径已经通过了格点\((i, j)\)，那么下一个通过的格点只可能是下列三种情况之一：\((i+1, j)\)，\((i, j+1)\)或者\((i+1, j+1)\)。

归整路径实际上就是满足上述约束的所有路径中，cumulative distances最小的那条路径，即：

\[D(i,j)=Dist(i,j)+\min(D(i-1,j),D(i,j-1),D(i-1,j-1)), D(1,1) = 0\]

这里的距离可以使用欧氏距离，也可以使用马氏距离。

DTW实例的具体计算过程可参见：

http://www.cnblogs.com/tornadomeet/archive/2012/03/23/2413363.html

从一个实例中学习DTW算法

从中可以看出，DTW实际上是一个动态规划问题。

更一般的，DTW也可用于计算两个离散的序列(不一定要与时间有关)的相似度。和《机器学习（二十二）》的EMD距离相比，DTW距离能够保持序列的形状信息。

除此之外，我们还可以增加别的约束：

全局路径窗口(Warping Window)：\(\mid \phi_x(s)-\phi_y(s)\mid \leq r\)。比较好的匹配路径往往在对角线附近，所以我们可以只考虑在对角线附近的一个区域寻找合适路径(r就是这个区域的宽度);

斜率约束(Slope Constrain)：\(\dfrac{\phi_x(m)-\phi_x(n)}{\phi_y(m)-\phi_y(n)}\leq p\)和\(\dfrac{\phi_y(m)-\phi_y(n)}{\phi_x(m)-\phi_x(n)}\leq q\)，这个可以看做是局部的Warping Window，用于避免路径太过平缓或陡峭，导致短的序列匹配到太长的序列或者太长的序列匹配到太短的序列。

上图是两种常见的约束搜索空间的方法。

DTW的缺点：

1.运算量大；

2.识别性能过分依赖于端点检测；

3.太依赖于说话人的原来发音；

4.不能对样本作动态训练；

5.没有充分利用语音信号的时序动态特性；

DTW适合于特定人基元较小的场合，多用于孤立词识别；

参考：

http://blog.csdn.net/zouxy09/article/details/9140207

动态时间规整（DTW）

https://blog.csdn.net/raym0ndkwan/article/details/45614813

DTW动态时间规整

http://www.cnblogs.com/luxiaoxun/archive/2013/05/09/3069036.html

Dynamic Time Warping动态时间规整算法

https://zhuanlan.zhihu.com/p/39450321

时间序列的搜索

https://blog.csdn.net/songbinxu/article/details/86660136

基于DTW相似度的Affinity Propagation(AP)聚类

https://zhuanlan.zhihu.com/p/72453060

动态时间规整下搜索和挖掘数万亿个时间序列子序列

https://mp.weixin.qq.com/s/ulS4lI3MZgcoDADF1sWnKA

DTW算法详解

https://mp.weixin.qq.com/s/pr-dUGaY-JxgUiu8HK5hqQ

时序数据DTW距离

Spectrogram

Window function

Fourier transform研究的是整个时间域和频率域的关系。因此它只能获取一段信号总体上包含哪些频率的成分，却对各成分出现的时刻并无所知。

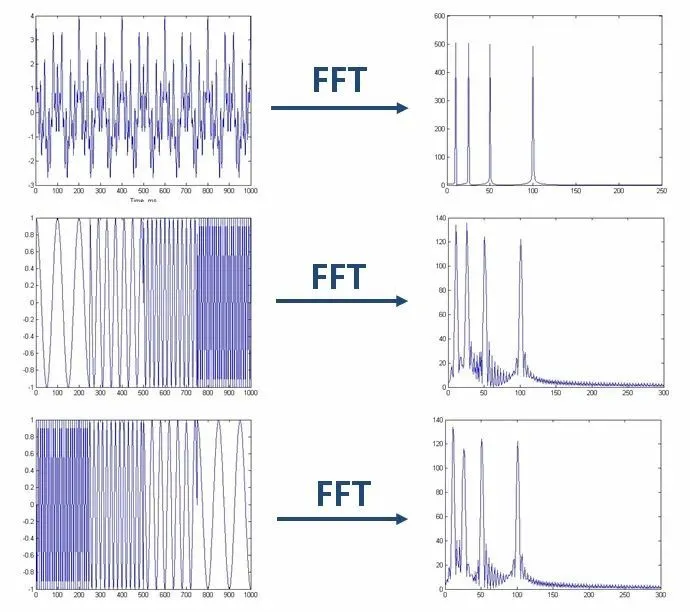
如上图所示的三个信号，虽然在时域上差异很大，但在频域上却是同一个信号。

此外，实际的信号处理过程，亦不可能对无限长的信号进行测量和运算，而是取其有限的时间片段进行分析。这时就需要从信号中截取一个时间片段，然后用截取的信号时间片段进行周期延拓处理，得到虚拟的无限长的信号，然后就可以对信号进行FT、相关分析等数学处理了。

无限长的信号被截断以后，其频谱发生了畸变，原来集中在f(0)处的能量被分散到两个较宽的频带中去了（这种现象称之为频谱能量泄漏）。

为了减少频谱能量泄漏，可采用不同的截取函数对信号进行截断，这些截断函数称为Window function。

常用的Window function有：Hann window、Rectangular window、Triangular window、Hamming window、Gaussian window等。

不同的窗函数对信号频谱的影响是不一样的。例如，Rectangular window主瓣窄，旁瓣大，频率识别精度最高，幅值识别精度最低；Blackman window主瓣宽，旁瓣小，频率识别精度最低，但幅值识别精度最高。

对Window function更详细的叙述参见：

https://en.wikipedia.org/wiki/Window_function

参考：

https://mp.weixin.qq.com/s/84f-HbQSvGPr2tD9EpdbVw

典型窗函数分析，对LFM信号进行时域和频域加窗对比

https://mp.weixin.qq.com/s/6F0cFHsHRasxNVlKty8GDQ

学好了傅立叶变换，你就能……做好一盘锅包肉