• Q-learning（续）
• Markov Decision Process
• 动态规划
  • 最优子结构
  • 重复子问题
  • RL与DP
    • Policy Iteration
    • Value Iteration

Q-learning（续）

Richard Ernest Bellman，1920～1984，美国应用数学家、控制论学家、数理生物学家。布鲁克林学院本科+威斯康星大学麦迪逊分校硕士+普林斯顿博士。二战期间曾在Los Alamos研究理论物理，后任职于美国智库RAND Corporation，南加州大学教授。美国艺术科学院、美国科学院院士。
Bellman–Ford算法的发明人之一。以他命名的奖项有Richard E. Bellman Control Heritage Award和Bellman Prize in Mathematical Biosciences。

在无监督的情况下，agent不断从一个状态转至另一状态进行探索，直到到达目标。我们将agent的每一次探索（从任意初始状态开始，经历若干action，直到到达目标状态的过程）称为一个episode。

Q-Learning算法的计算步骤如下：

Step 1：给定参数\(\gamma\)和reward矩阵R。
Step 2：初始化Q=0。
Step 3：For each episode:

3.1 随机选择一个初始状态s。
3.2 若未达到目标状态，则：

(1)在当前s的所有action中，随机选择一个行为a。
(2)利用a，得到下一个状态\(\tilde s\)。
(3)利用公式1，计算\(Q(s,a)\)。
(4)令\(s=\tilde s\)。

由马尔可夫过程的性质（参见《机器学习（二十六）》）可知，Q矩阵最终会趋于一个极限，如下所示：

上面的矩阵可用下图表示：

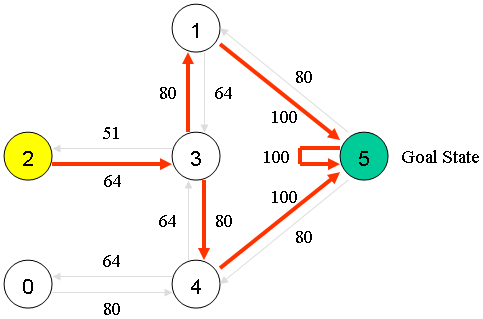
显然，沿着Q值最大的边走，就是这个探索问题的最佳答案。（如上图红线所示）即：

\[\pi (s)=\arg \max_a(Q(s,a))\]

参考：

http://blog.csdn.net/itplus/article/details/9361915

一个Q-learning算法的简明教程

http://blog.csdn.net/young_gy/article/details/73485518

强化学习之Q-learning简介

https://mp.weixin.qq.com/s/34E1tEQMZuaxvZA66_HRwA

通过Q-learning深入理解强化学习

https://mp.weixin.qq.com/s/kmk3mKASZPixA8VS9sipcA

走近流行强化学习算法：最优Q-Learning

https://mp.weixin.qq.com/s/o-IzYt62qaUhcTY33E0Ylg

基于强化学习Q-Learning模型构建算法交易策略

https://mp.weixin.qq.com/s/ePssT5BDb9KebCTehn0ugw

5分钟读懂强化学习之Q-learning

https://www.zhihu.com/question/26408259

如何用简单例子讲解Q-learning的具体过程？

Markov Decision Process

上边Q-Learning的例子中，由于action能够唯一确定状态的变换，因此又被称为Markov Reward Process：

\[<\mathcal{S},\mathcal{P},\mathcal{R},\gamma>\]

这个四元组依次代表：states、state transition probability matrix、reward function、discount factor。

实际中，执行特定的动作并不一定能得到特定的状态。

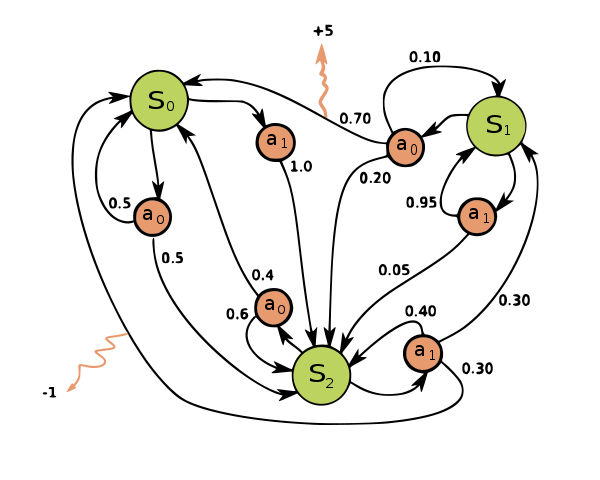
比如上图中，在状态\(S_0\)，执行\(a_0\)，只有0.5的机会，会到达\(S_2\)。这也就是之前提到过的MDP。

标准MDP中的Bellman equation可改为如下形式：

\[v = \mathcal{R} + \gamma \mathcal{P}v\]

其中,\(\mathcal{P},\mathcal{R}\)均为已知。

这里的Bellman equation是线性方程，它的直接解法如下：

\[(I-\gamma \mathcal{P})v = \mathcal{R}\] \[v = (I-\gamma \mathcal{P})^{-1}\mathcal{R}\]

然而这个方法的复杂度是\(O(n^3)\)（n是状态的个数），这对于大的MDP来说，并不好用。这种情况下，常用的解法有：Dynamic programming（动态规划）、Monte-Carlo evaluation和Temporal-Difference learning。

由于MDP对于RL任务进行了Markov假设，这属于一种建模行为，因此它也被归为一种model-based learning的算法。

MDP的扩展主要包括：

a) Observation部分可见的情况下，agent state \(\neq\) environment state，这时一般叫做partially observable Markov decision process(POMDP)。

b) Infinite and continuous MDP

c) Undiscounted, average reward MDP

扩展MDP的Bellman equation都不是线性方程，没有解析解，只有迭代解。相关解法主要使用了概念图模型，这里不再详述。

参考：

https://mp.weixin.qq.com/s/G8zmooqhSKqcLv1u7uM0bw

AlphaGo等智能体是如何炼成的？你需要懂得马尔科夫链

https://mp.weixin.qq.com/s/KQmKb5NrjgxooCnbZaiTzw

强化学习中无处不在的贝尔曼最优性方程，背后的数学原理为何？

动态规划

Dynamic programming(DP)用于解决那些可分解为重复子问题（overlapping subproblems）并具有最优子结构（optimal substructure）的问题。这里的programming和编程并无任何关系。

上世纪40年代，Richard Bellman最早使用动态规划这一概念表述通过遍历寻找最优决策解问题的求解过程。1953年，Richard Bellman将动态规划赋予现代意义，该领域被IEEE纳入系统分析和工程中。

除了Bellman之外，苏联的Lev Pontryagin也做出了很大的贡献，他和Bellman被并称为Optimal control之父。

Lev Semyonovich Pontryagin，1908~1988，苏联数学家。主要研究代数拓扑和微分拓扑。他14岁时，因为煤气爆炸事故成为盲人。苏联科学院院士，国际数学家联盟副主席。

最优子结构

最优子结构即可用来寻找整个问题最优解的子问题的最优解。举例来说，寻找图上某顶点到终点的最短路径，可先计算该顶点所有相邻顶点至终点的最短路径，然后以此来选择最佳整体路径，如下图所示：

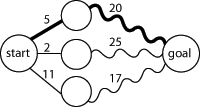
一般而言，最优子结构通过如下三个步骤解决问题：

a) 将问题分解成较小的子问题；

b) 通过递归使用这三个步骤求出子问题的最优解；

c) 使用这些最优解构造初始问题的最优解。

子问题的求解是通过不断划分为更小的子问题实现的，直至我们可以在常数时间内求解。

重复子问题

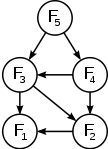
重复子问题是指通过相同的子问题可以解决不同的较大问题。例如，在Fibonacci序列中，F3 = F1 + F2和F4 = F2 + F3都包含计算F2。由于计算F5需要计算F3和F4，一个比较笨的计算F5的方法可能会重复计算F2两次甚至两次以上。

为避免重复计算，可将已经得到的子问题的解保存起来，当我们要解决相同的子问题时，重用即可。该方法即所谓的缓存（memoization）。

动态规划通常采用以下两种方式中的一种：

自顶向下：将问题划分为若干子问题，求解这些子问题并保存结果以免重复计算。该方法将递归和缓存结合在一起。

自下而上：先行求解所有可能用到的子问题，然后用其构造更大问题的解。该方法在节省堆栈空间和减少函数调用数量上略有优势，但有时想找出给定问题的所有子问题并不那么直观。

需要注意的是：动态规划更多的看作是一种解决问题的方法论，而非具体的数值算法，因此，很多不同领域的算法都可看做是动态规划算法的实例。参考文献中，就列出了不少这样的算法。显然，动态规划是一种迭代（Iteration）算法。

由前文的描述可知，MDP正好具备overlapping subproblems和optimal substructure的特性，因此也可以通过DP求解。

在继续下文之前，推荐一波资源：

David Poole，加拿大不列颠哥伦比亚大学教授。加拿大AI协会终身成就奖（2013年）。
个人主页：
http://www.cs.ubc.ca/~poole/index.html

David Poole的主页上有很多好东西：

http://www.cs.ubc.ca/~poole/demos/

该网页上有一些RL方面的用java applet做的可视化demo。由于年代比较久远，这些demo无法在目前的浏览器上运行。所以，我对其做了一些改造，使之能够使用。相关代码参见：

https://github.com/antkillerfarm/antkillerfarm_crazy/tree/master/RL

2019.10
由于appletviewer在最新的JDK中已经被移除了，因此，这次选择JS作为目标语言，并对其中的Q-Learning做了移植。
代码：
https://github.com/antkillerfarm/antkillerfarm_crazy/tree/master/nodejs/js/RL/Q

David Poole还写了一本书《Artificial Intelligence: foundations of computational agents》，目前已经是第2版了。

其中的代码资源参见：

http://artint.info/AIPython/

从该书所用编程语言的变迁，亦可感受到Poole教授不断学习的脚步。要知道Poole教授刚进入学术界的时代（1985年前后），就连Java也还没被发明出来呢。

http://uhaweb.hartford.edu/compsci/ccli/samplep.htm

Hartford大学的这个网站也有些不错的资料，偏重RL、机器人、ML for Game等领域。

RL与DP

在继续讲述之前，我们首先来明确几个概念：

\(v_{\pi}\)和\(q_{\pi}\)的定义参见《强化学习（一）》。

\[v_*(s)=\max_{\pi}v_{\pi}(s)\] \[q_*(s,a)=\max_{\pi}q_{\pi}(s,a)\]

RL领域的DP算法的主要思想是：利用value function构建搜索Good Policy的方法。这里用\(v_*(s)\)或\(q_*(s, a)\)表示最优的value function。

RL DP主要包括以下算法：（为了抓住问题的本质，这里仅列出各算法最关键的Bellman equation，至于流程参照Q-learning算法即可。）

Policy Iteration

Policy Iteration包含如下两步：

Policy Evaluation：

\[v_{k+1}(s) = \sum_{a \in \mathcal{A}}\pi(a \mid s)\left(\mathcal{R}_s^a + \gamma \sum_{s'\in \mathcal{S}}\mathcal{P}_{ss'}^a v_k(s')\right)\]

Policy Improvement：

\[\pi_{k+1}(s) = \arg \max_{a \in \mathcal{A}}\left(\mathcal{R}_s^a + \gamma \sum_{s'\in \mathcal{S}}\mathcal{P}_{ss'}^a v_k(s')\right)\]

由于\(q_*(s, a)\)对应的\(v(s)\)必是\(v_*(s)\)，反之亦然，因此Policy Iteration的过程通常如下所示：

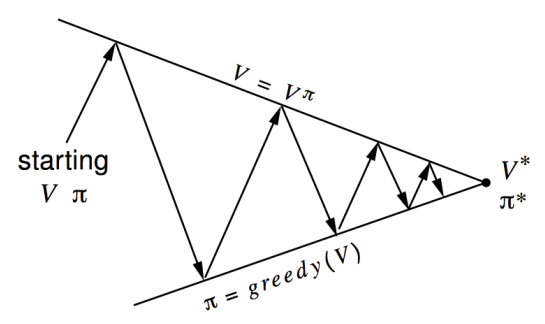
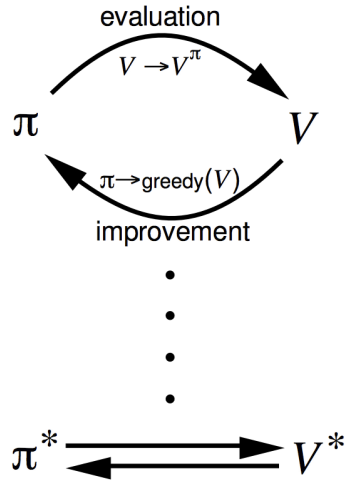
如果只需要Prediction，不需要Control的话，也可以只进行Policy Evaluation，这时也被称为Iterative Policy Evaluation。

Value Iteration

\[v_{k+1}(s) = \max_{a \in \mathcal{A}}\left(\mathcal{R}_s^a + \gamma \sum_{s'\in \mathcal{S}}\mathcal{P}_{ss'}^a v_k(s')\right)\]

state-value function迭代的复杂度是\(O(mn^2)\)，其中m为action的数量，n为state的数量。而action-value function迭代的复杂度是\(O(m^2n^2)\)

Policy Iteration与Value Iteration的区别在于：

1.Policy Iteration是在迭代过程中不断寻找最优策略。

2.Value Iteration是在迭代过程中寻找状态s下的最优value。如果所有状态的最优value都找到的话，则可通过寻找最大value路径的方式，找到最优策略。例如，之前提到的Q-Learning。

动态规划的主要局限在于：

1.它依赖于概率模型。

2.计算复杂度太高，只适合规模中等（<1M的状态数）的情况。