• Actor-Critic
  • Reducing Variance Using Baseline（续）
  • 参考
• 博弈论
  • 历史
  • 教程
  • 概述
  • 囚徒困境
  • 帕累托最优
  • 纳什均衡

Actor-Critic

Reducing Variance Using Baseline（续）

根据定义，TD误差\(\delta^{\pi_\theta}\)可以根据真实的状态价值函数\(V^{\pi_\theta}(s)\)算出：

\[\delta^{\pi_\theta} = r + \gamma V^{\pi_\theta}(s') - V^{\pi_\theta}(s)\]

因为：

\[\begin{align} E_{\pi_\theta}[\delta^{\pi_\theta} | s,a] &= E_{\pi_\theta}[r + \gamma V^{\pi_\theta}(s') | s,a] - V^{\pi_\theta}(s)\\ &= Q^{\pi_\theta}(s,a) - V^{\pi_\theta}(s) \\ &= A^{\pi_\theta}(s,a) \end{align}\]

可见\(\delta^{\pi_\theta}\)就是\(A^{\pi_\theta}(s,a)\)的一个无偏估计。

因此，我们就可以使用TD误差来计算策略梯度：

\[\nabla_\theta J(\theta)= E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a)\delta^{\pi_\theta}]\]

实际运用时，我们使用一个近似的TD误差，即用状态函数的近似函数来代替实际的状态函数：

\[\delta_v = r + \gamma V_v(s') - V_v(s)\]

这也就是说，我们只需要一套参数描述状态价值函数，而不再需要行为价值函数了。

上述方法不仅可用于TD方法，还可用于MC方法等，以下不加讨论的给出如下结论：

\[\begin{align} \nabla_\theta J(\theta) &= E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a){\color{red}{v_t}}] & \text{REINFORCE}\\ &= E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a){\color{red}{Q_w(s,a)}}] & \text{Q Actor-Critic}\\ &= E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a){\color{red}{A_w(s,a)}}] & \text{Advantage Actor-Critic}\\ &= E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a){\color{red}{\delta}}] & \text{TD Actor-Critic}\\ &= E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a){\color{red}{\delta e}}] & \text{TD(}\lambda\text{) Actor-Critic} \end{align}\]

参考

https://zhuanlan.zhihu.com/p/51652845

强化学习这都学不会的话，咳咳，你过来下！

https://mp.weixin.qq.com/s/ce9W3FbLdsqAEyvw6px_RA

Actor Critic——一个融合基于策略梯度和基于值优点的强化学习算法

https://mp.weixin.qq.com/s/BZUlUKkPMAP5r6HFJQq8-A

全面总结(值函数与优势函数)的估计方法

博弈论

博弈论（game theory）是一门单独的学科，和RL并无统属关系。然而由于RL，特别是MARL大量应用到了相关的知识，所以这里也把它写在RL系列里了。

历史

博弈论最早可追溯到“齐威王田忌赛马”，但它真正的发展是在20世纪下半叶。

RL的历史相对比较晚，因此从渊源来看，RL=博弈论+控制论+ML。

参考：

https://blog.csdn.net/sobermineded/article/details/79601986

博弈论历史、发展与应用

教程

《Game Theory: An Introduction》，Steven Tadelis著。

Steven Tadelis，经济学家。Harvard博士（1997），UCB教授。

https://mp.weixin.qq.com/s/U_vDI_PJm-buubTwJgV9pw

数学博弈论与应用，431页pdf，Mathematical Game Theory and Applications

https://github.com/cheat-sheets/game-theory-cheat-sheet

一个博弈论方面的Cheat Sheet。

概述

要理解博弈论，可以通过博弈论和决策论的区别开始。

决策论是研究局中人在给定其他环境参数条件下的最优选择问题。

博弈论研究的是当局中人充分考虑到其他局中人对其战略选择的反应后（即局中人都具有同样充分的理性时）进行最优战略的选择。

博弈论的直接目标不是找到一个玩家的最佳策略，而是找到所有玩家的最理性策略组合。我们称最理性策略组合为均衡（equilibrium）。

从宏观上可以将博弈论研究的问题分为：合作博弈和非合作博弈。现代狭义的博弈论一般是指非合作博弈。

非合作博弈根据参与博弈的参与人做决策的先后顺序可以分为：静态博弈和动态博弈。

静态博弈：参与人同时做决策，常用标准型（normal form）表述其策略。如两人零和博弈等。

动态博弈：参与人有先后顺序做决策，且后者能观察到前者所做的决策，如围棋等。常用扩展型（extensive form）来表述其策略，常用的扩展型表述为博弈树。

非合作博弈根据参与人是否已知对方的信息，可以分为：完美信息博弈和不完美信息博弈。

完美信息博弈：参与人对相关信息完全已知，如棋类游戏。玩家知道对方棋子所在的位置。

不完美信息博弈：参与人对相关信息并不完全已知。如牌类游戏，玩家并不知道对手的牌是什么。

当局中人的个数n为有限数且每个局中人的战略空间中的元素只有限个时，称博弈为有限博弈（finite game）。

决策问题的三要素：

• 行动(action): 玩家可能的选择
• 结果(outcome): 每个行动的可能后果
• 倾向(preference): 对所有可能后果，按照从最渴望到最不渴望的排列。

理智选择假设：

一个玩家完全明白决策问题：

• 所有可能的行动
• 所有可能的结果
• 了解行动如何影响结果
• 玩家的理性倾向（收益）是基于结果的

经济人(Homo economicus)：一个经济人是理智的，了解决策问题的各个因素，并且总是选择可以获得最高收益的行动。

风险态度：

• 中立风险（risk neutral）：认为同样期望回报的价值相同。
• 厌恶风险（risk averse）：倾向于一个确定性的回报，不愿意采用一个拥有同样期望回报的不确定性方案。
• 喜爱风险（risk loving）：更严格地倾向于采用拥有同样期望回报的赌注。

博弈论旨在了解游戏的动态，以优化其玩家可能获得的结果。相反的，逆博弈论（Inverse Game Theory）旨在根据玩家的策略和目标来设计游戏。逆博弈论在多智能体AI以及人机交互AI中都很有用处。

囚徒困境

上图是囚徒困境（prisoner’s dilemma）的策略矩阵。

参与者为：囚徒A和囚徒B。动作空间为：{坦白、抵赖}，回报函数由矩阵给出。即：

• 当囚徒A和囚徒B都坦白时，囚徒A被判处3年有期徒刑、囚徒B也被判处3年有期徒刑。
• 当囚徒A坦白、囚徒B抵赖时，囚徒A被当场释放、囚徒B被判处5年有期徒刑。
• 当囚徒A抵赖、囚徒B坦白时，囚徒A被判处5年有期徒刑、囚徒B当场释放。
• 当囚徒A抵赖、囚徒B抵赖时，囚徒A和B都被判处1年有期徒刑。

很明显，如果两个囚徒都选择抵赖，那么它们总的惩罚最低。然而，选择抵赖对于囚徒个人来说是理性的吗？

答案是：选择抵赖对于个人来说并不理性。因为，就个人而言，囚徒并不知道另外一个囚徒选择的策略是什么。在这种情况下，选择坦白对于个人来说是理性的，而且是最优的。

即，不管其他囚徒选择什么动作，选择坦白总比选择抵赖要优。

比如，对于囚徒A来说：

当囚徒B选择坦白时，如果囚徒A选择坦白被判处3年有期徒刑；而这时如果A选择抵赖则被判处5年有期徒刑，所以这时囚徒A选择坦白要好。

当囚徒B选择抵赖时，如果囚徒A选择坦白，则当场释放；而这时如果A选择抵赖，则被判处1年有期徒刑，所以这时囚徒A选择坦白要好。

综合这两种情况，对于囚徒A不管囚徒B如何选择，选择坦白都是最好的。

在该例中（坦白，坦白）是占优策略（dominated strategy）。所谓占优策略是指如果一方在任何情况下从某种策略中得到的回报均大于从另外一种策略得到的回报，那么我们称为这种策略为占优策略。

囚徒困境同样适于分析寡头垄断厂商合作的不稳定性。对于寡头整体而言最理性的做法是（合作，合作）。于是，诸如OPEC等组织会联手以期达到利润最大化。但同时，另外有种激励，若自己悄悄毁约、不遵守协议自己的获利会高于合作下的获利。于是（不合作，不合作）的策略组合排挤掉了（合作，合作）的策略组合，并且由于（不合作，不合作）组合还是一个占优策略均衡，所以，卡特尔经常以失败告终，也就属情理之中了。

帕累托最优

帕累托最优(Pareto Optimality)，也称为帕累托效率(Pareto efficiency)，是指资源分配的一种理想状态，假定固有的一群人和可分配的资源，从一种分配状态到另一种状态的变化中，在没有使任何人境况变坏的前提下，使得至少一个人变得更好。帕累托最优状态就是不可能再有更多的帕累托改进的余地;换句话说，帕累托改进是达到帕累托最优的路径和方法。 帕累托最优是公平与效率的”理想王国”。

Vilfredo Pareto，1848~1923，意大利经济学家、社会学家。

参考：

https://www.zhihu.com/question/414629107

帕累托最优和功利主义有区别吗?

纳什均衡

Nash equilibrium的定义：

在博弈中，如果联结策略\((\pi^*_1,\dots,\pi^*_n)\)满足：

\[V_i(\pi^*_1,\dots,\pi^*_i,\dots,\pi^*_n)\ge V_i(\pi^*_1,\dots,\pi_i,\dots,\pi^*_n),\forall \pi_i \in \Pi_i, i=1,\dots,n\]

则为一个纳什均衡。若上式严格大于，则为严格纳什均衡。

若智能体的策略对一个动作的概率分布为1，对其余的动作的概率分布为0，则这个策略为一个纯策略。

若一个策略对于智能体动作集中的所有动作的概率都大于0，则这个策略为一个完全混合策略。

介于上述两者之间的叫做混合策略。

纳什存在定理(Nash’s existence Theorem)：

任何普通形式、具有限策略集合的博弈存在一个纳什均衡的混合策略。

零和博弈中，两个智能体是完全竞争对抗关系，它只有一个纳什均衡值，即使可能有很多纳什均衡策略，但是期望的奖励是相同的。

一般和博弈是指任何类型的矩阵博弈，包括完全对抗博弈、完全合作博弈以及二者的混合博弈。在一般和博弈中可能存在多个纳什均衡点。

下图是纳什均衡的几何解释：

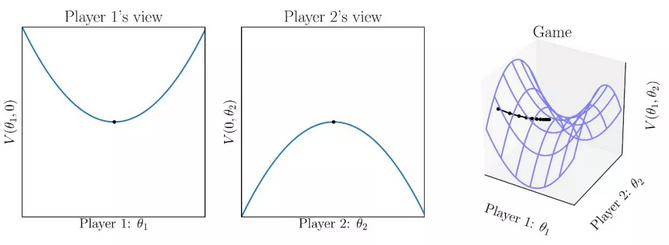
John Nash，1928～2015，数学家、经济学家。Princeton博士（1950），Princeton教授。主要研究博弈论、微分几何学和偏微分方程。诺贝尔经济学奖获得者（1994）。奥斯卡金像奖电影《美丽心灵》男主角原型。

参考：

https://mp.weixin.qq.com/s/pTGPIm8msErFCZEUz2n2Gw

鞍点问题及纳什均衡问题的新研究成果