RL » 强化学习(二)——K-摇臂赌博机, Q-learning
2018-11-23 :: 5651 Words概述(续)
Policy, Value, Transition Model
增强学习中,比较重要的几个概念:
Policy:我们的算法追求的目标,可以看做一个函数,在输入state的时候,能够返回此时应该执行的action或者action的概率分布。
\[\pi(a \mid s) = P[A_t = a \mid S_t = s]\]Value:价值函数,表示在输入state,action的时候,能够返回在state下,执行这个action能得到的Discounted future reward的(期望)值。
Value function一般有两种。
state-value function:
\[v_{\pi}(s) = E_{\pi} [G_t \mid S_t = s]\]action-value function:
\[q_{\pi}(s; a) = E_{\pi} [G_t \mid S_t = s; A_t = a]\]后者由于和state、action都有关系,也被称作state-action pair value function。
Transition model:环境本身的结构与特性。当在state执行action的时候,系统会进入的下一个state,也包括可能收到的reward。
很显然,以上三者互相关联:
如果能得到一个好的Policy function的话,那算法的目的已经达到了。
如果能得到一个好的Value function的话,那么就可以在这个state下,选取value值高的那个action,自然也是一个较好的策略。
如果能得到一个好的transition model的话,一方面,有可能可以通过这个transition model直接推演出最佳的策略;另一方面,也可以用来指导policy function或者value function的学习过程。
因此,增强学习的方法,大体可以分为三类:
Value-based RL,值方法。显式地构造一个model来表示值函数Q,找到最优策略对应的Q函数,自然就找到了最优策略。
Policy-based RL,策略方法。显式地构造一个model来表示策略函数,然后去寻找能最大化discounted future reward的策略。
Model-based RL,基于环境模型的方法。先得到关于environment transition的model,然后再根据这个model去寻求最佳的策略。
以上三种方法并不是一个严格的划分,很多RL算法同时具有一种以上的特性。
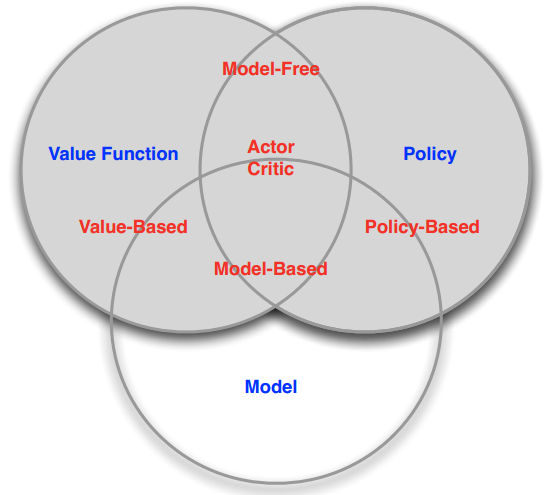
比如,Actor-Critic(演员-评判家)方法:agent既有价值函数、也有策略函数。两者相互结合解决问题。
参考
https://mp.weixin.qq.com/s/f6sq8cSaU1cuzt7jhsK8Ig
强化学习(Reinforcement Learning)基础介绍
https://mp.weixin.qq.com/s/TGN6Zhrea2LPxdkspVTlAw
穆黎森:算法工程师入门——增强学习
https://mp.weixin.qq.com/s/laKJ_jfNR5L1uMML9wkS1A
强化学习(Reinforcement Learning)算法基础及分类
https://mp.weixin.qq.com/s/Cvk_cePK9iQd8JIKKDDrmQ
强化学习的核心基础概念及实现
http://mp.weixin.qq.com/s/gHM7qh7UTKzatdg34cgfDQ
强化学习全解
https://mp.weixin.qq.com/s/B6ZpJ0Yw9GBZ9_MyNwjlXQ
构建强化学习系统,你需要先了解这些背景知识
https://zhuanlan.zhihu.com/p/146212198
强化学习经典算法理论
https://mp.weixin.qq.com/s/AKuuIJnESMmck8k210CnWg
易忽略的强化学习知识之基础知识及MDP(上)
https://mp.weixin.qq.com/s/phuCKNj_a4CPq6w51Md-9A
易忽略的强化学习知识之基础知识及MDP(下)
https://mp.weixin.qq.com/s/QHAnpGsr1sSaUgOXTJjVjQ
李飞飞高徒带你一文读懂RL来龙去脉
https://mp.weixin.qq.com/s/iN8q24ka762LqY74zoVFsg
3万字剖析强化学习在电商环境下应用
https://mp.weixin.qq.com/s/qhRxZTq0IdMonAeNj25K1Q
马尔科夫决策过程之Markov Processes
https://mp.weixin.qq.com/s/s-6utyFffAdHOkjadzXYwg
强化学习:Policy-based方法Part1
https://mp.weixin.qq.com/s/wMwqDfIAdDyeeE_ZnBh0zg
强化学习:Policy-based方法Part2
https://zhuanlan.zhihu.com/p/54985200
用有趣的文字,教你强化学习入门知识(上)
https://zhuanlan.zhihu.com/p/55671989
用有趣的文字,教你强化学习入门知识(下)
https://mp.weixin.qq.com/s/zNJ4Au_aVTxeIpn-VHt-tA
强化学习奖励函数设计与设置的几种方法
K-摇臂赌博机

k-armed Bandit(也叫Multi-Armed Bandit)是赌场里的一种赌具。它有K个摇臂,投币后摇动摇臂,会有一定的概率吐出硬币。每个摇臂的吐币概率和数量有所不同。(有的机器只有1个摇臂,但可通过按钮设置不同的方案。)赌徒的目标是通过一定的策略获得最多的奖励(硬币)。
尽管在有的赌场中,每个摇臂的吐币概率和数量是已知的,但在本问题中,吐币概率和数量都是未知的。
由于每次摇臂都是独立事件,因此k-armed Bandit问题的另一个约束是:最大化单步奖励,即不考虑未来的奖励。
此外,k-armed Bandit亦不可能无限进行下去,其尝试总数是一定的(即投币数是一定的)。这也是该问题的一个隐含约束。
这里显然有两个最简单的策略:
exploration-only:将所有尝试机会平均分配给每个摇臂。这种策略可以很好的估计每个摇臂的奖励,然而却会失去很多选择最优摇臂的机会。
exploitation-only:只按下目前最优的摇臂。这种策略下有可能选不到最优的摇臂。
显然,欲奖励最大,需要在exploration和exploitation之间达成较好的折中。
\(\epsilon\)-贪心算法
\(\epsilon\)-greedy基于概率对exploration和exploitation进行折中,即:以\(\epsilon\)进行exploration,而以\(1-\epsilon\)进行exploitation。
若摇臂奖励的不确定性较大,即概率分布较宽时,需要较大的\(\epsilon\)值,反之则小。
另外,开始时由各种信息较少,\(\epsilon\)需要设置的大一些,随着探索的深入,各摇臂的奖励基本弄清楚之后,\(\epsilon\)就可以小一些了。因此通常令\(\epsilon=1/\sqrt{t}\)。
当\(\epsilon=0\)时,该算法也被称为greedy算法,也就是之前提到的exploitation-only策略。
必须指出的是,k-armed Bandit只是真实问题的一个极度简化模型:它只有action和reward,没有input或sequentiality,也没有state。
Softmax算法
Softmax算法和\(\epsilon\)-贪心算法类似,其公式为:
\[P(k)=\frac{e^{\frac{Q(k)}{\tau}}}{\sum_{i=1}^{K}e^{\frac{Q(i)}{\tau}}}\]这实际上是一个Boltzmann分布的公式,其中\(\tau\)表示温度,\(\tau \to 0\)表示优先利用,\(\tau \to \infty\)表示优先探索。
\(\epsilon\)-greedy采用随机选择策略,因此,除了最优解之外的其他解被选择的概率相等。显然,这种策略并没有使用到历史信息。
而Softmax算法则根据回报率选择臂杆,回报率比最大值小很多的臂杆很少选中,回报率接近最大值的笔杆被选中的概率接近最大臂被选中的概率。这种策略虽然考虑了一部分历史信息,但如果最优解的臂杆第一次碰巧给了很差的回报的话,最终的结果就很难最优了。
求均值的小技巧
在k-armed Bandit问题中,一般用reward的均值来近似它的数学期望值。由于action是个序列,因此相应的算法一般是个不断迭代的过程,或者也可以说是一个增量(incremental)过程。
在增量过程中,保存所有的reward值来计算均值显然是个笨办法。这里常用的办法是:
\[Q_{n+1}=Q_n+\frac{1}{n}[R_n-Q_n]\]不光reward值可以这样更新,其他均值也可采用这个方法:
\[NewEstimate \leftarrow OldEstimate + StepSize [Target - OldEstimate]\]非平稳问题
在之前的假设中,我们认为每个摇臂的吐币概率和数量是不随时间变化的,这样的问题被称为Stationary Problem。
如果每个摇臂的吐币概率和数量随时间缓慢变化的话,则称之为Non-stationary Problem。
快速变化的系统,不光RL无能,其他方法估计也没什么好效果。所以系统保持一定的惯性,对于研究问题是很重要的。
这时一般采用如下公式滤波:
\[Q_{n+1}=Q_n+\alpha[R_n-Q_n]\]详细内容参见《数学狂想曲(十四)》的“软件滤波算法”一节的“一阶滞后滤波法”和“加权递推平均滤波法”。
Gradient-Bandit算法
Gradient-Bandit算法的定义如下:
\[Pr\{A_t=a\}=\frac{e^{H_t(a)}}{\sum_{b=1}^ke^{H_t(b)}}=\pi_t(a)\] \[H_{t+1}(a)=H_t(a)+\alpha(R_t-\overline R_t)(1\{A_t=a\}-\pi_t(a))\] \[\overline R_t=\frac{1}{t}\sum_{i=1}^tR_i\]其中,\(H_t(a)\)被称作策略偏好(preference)。这实际上是一个Softmax算法的变种。
多步强化学习
对于多步强化学习任务,虽然可以将其中的每一步看作一个k-armed Bandit问题,然而由于这种方法忽视了决策过程之间的联系,存在很多局限,因此不如MDP相关的算法。
参考
http://www.xfyun.cn/share/?p=2606
Bandit算法与推荐系统
https://mp.weixin.qq.com/s/9dXqXmRkINjwJYB4csjU5A
强化学习初探-从多臂老虎机问题说起
https://mp.weixin.qq.com/s/lN-2ORkfx5C3TiX_VMdaDA
Bandit算法在携程推荐系统中的应用与实践
https://mp.weixin.qq.com/s/6zzOU_hrtAGFPnDz2KuqVg
基于强化学习的Contextual Bandits算法在推荐场景中的应用
Q-learning
Q-learning是强化学习中很重要的算法,也是最早被引入DL领域的强化学习算法,对它的研究催生了Deep Q-learning Networks。
下面用一个例子来讲述Q-learning算法。
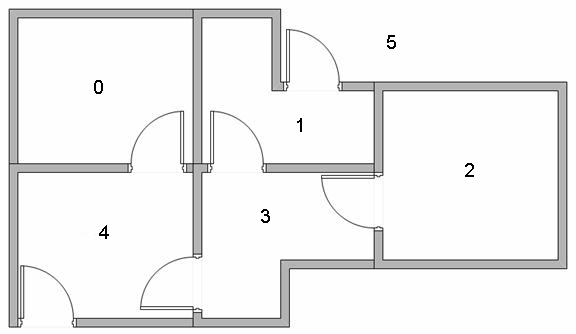
上图中有5个房间,编号为0~4,将户外定义为编号5,房间之间通过门相连,则房间的联通关系可抽象为下图:
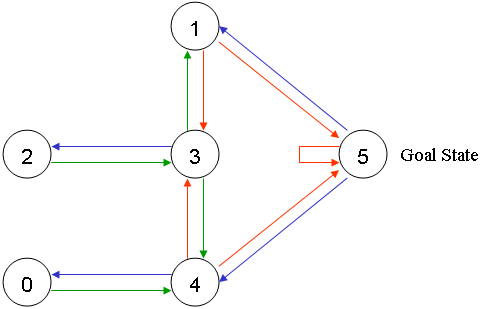
这里我们将每个房间称为一个state,将agent从一个房间到另一个房间称为一个action。
开始时,我们将agent放置在任意房间中,并设定目标——走到户外(即房间5),则上图可变为:
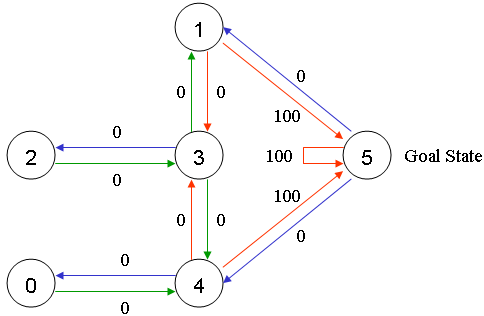
这里的每条边上的数值就是reward值。Q-Learning的目标就是达到reward值最大的state。因此当agent到达户外之后,它就停留在那里了,这样的目标被称作吸收目标。
如果以state为行,action为列,则上图又可转化为如下的reward矩阵:
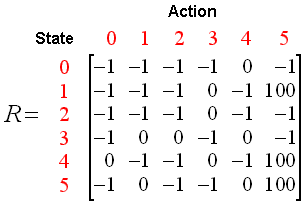
其中,-1表示两个state之间没有action。
类似的,我们可以构建一个和R同阶的矩阵Q,来表示Q-Learning算法学到的知识。
开始时,agent对外界一无所知,所以Q可以初始化为零矩阵。
Q-Learning算法的transition rule为:
\[Q(s,a)=R(s,a)+\gamma \max(Q(\tilde s,\tilde a))\tag{1}\]其中,(s,a)表示当前的state和action,\((\tilde s,\tilde a)\)表示下一个state和action,\(0 \le \gamma < 1\)为学习参数。这个公式也被称作Bellman equation。

您的打赏,是对我的鼓励
