math » 数学狂想曲(十四)——数学的深渊, Wavelet & Chirplet, Lanchester战争模型
2019-10-06 :: 5172 Words软件滤波算法(续)
限幅平均滤波法
方法:相当于“限幅滤波法”+“递推平均滤波法”,每次采样到的新数据先进行限幅处理,再送入队列进行递推平均滤波处理。
优点:融合了两种滤波法的优点,对于偶然出现的脉冲性干扰,可消弭由于脉冲干扰所惹起的采样值偏差。
缺点:比较浪费RAM。
一阶滞后滤波法
方法:取a=0~1,本次滤波结果=(1-a)本次采样值+a上次滤波结果。
优点:对周期性干扰具有良好的抑制造用,适用于波动频率较高的场合。
缺点:相位滞后,灵敏度低,滞后程度取决于a值大小,不能消弭滤波频率高于采样频率的1/2的干扰信号。
加权递推平均滤波法
方法:这是对递推平均滤波法的改进,即不同时刻的数据加以不同的权,通常是,越接近现时刻的材料,权取得越大,给予新采样值的权系数越大,则灵敏度越高,但信号平滑度越低。
优点:适用于有较大纯滞后事件常数的对象和采样周期较短的系统。
缺点:对于纯滞后事件常数较小,采样周期较长,变化缓慢的信号,不能迅速反应系统当前所受干扰的严重程度,滤波效果差。
消抖滤波法
方法:设置一个滤波计数器,将每次采样值与当前有效值比较:如果采样值等于当前有效值,则计数器清零。如果采样值不等于当前有效值,则计数器+1,并判断计数器能否>=下限N(溢出),如果计数器溢出,则将本次值交换当前有效值,并清计数器。
优点:对于变化缓慢的被测参数有较好的滤波效果,可避免在临界值附近控制器的反复开/关跳动或显示器上数值抖动。
缺点:对于快速变化的参数不宜,如果在计数器溢出的那一次采样到的值恰好是干扰值,则会将干扰值当作有效值导入系统。
限幅消抖滤波法
方法:相当于“限幅滤波法”+“消抖滤波法”,先限幅后消抖。
优点:承继了“限幅”和“消抖”的优点,改进了“消抖滤波法”中的某些缺陷,避免将干扰值导入系统。
缺点:对于快速变化的参数不宜。
IIR数字滤波
方法:确定信号带宽,滤之。
\[Y(n)=a_1*Y(n-1)+a_2*Y(n-2)+...+a_k*Y(n-k)+\] \[b_0*X(n)+b_1*X(n-1)+b_2*X(n-2)+...+b_k*X(n-k)\]优点:高通,低通,带通,带阻任意。design简单(用matlab)。
缺点:运算量大。
数学的深渊

当然,类似的还有个AI的深渊:

最近(2019.7)新出了一个加强版的数学的深渊:






















其他深渊:
https://mp.weixin.qq.com/s/l1_Met_1mCltmoJ-ISWeSg
压力太大,不想工作?那就下海摸鱼吧
https://mp.weixin.qq.com/s/UJH2vSmsRnF2zyiuAr4zmg
太震撼了!2600年数学文明画在了一张图上
一道证明题
设A、B、C为任意可数有限集合,则
\[size(A-C)\le size(A-B)+size(B-C)\]其中\(size(X)\)表示集合X中的元素个数。
证明:
\[\begin{array}\\ A-C=\{x\mid x\in A \cap x\notin C\}=\{x\mid x\in A \cap (x\in B \cup x\notin B)\cap x\notin C\}\\ =\{x\mid (x\in A \cap x\notin B \cap x\notin C) \cup (x\in A \cap x\in B \cap x\notin C) \}\\ \subseteq \{x\mid (x\in A \cap x\notin B) \cup (x\in B \cap x\notin C) \}=(A-B)\cup (B-C) \end{array}\]又因为:\(size(X\cup Y)\le size(X)+size(Y)\),所以
\[size(A-C)\le size((A-B)\cup (B-C))\le size(A-B)+size(B-C)\]莫比乌斯反演
August Ferdinand Möbius,1790~1868,德国数学家、天文学家。University of Leipzig毕业后,曾在University of Göttingen访学,导师Gauss。University of Leipzig教授,Leipzig天文台台长。
http://blog.csdn.net/acdreamers/article/details/8542292
莫比乌斯反演
http://blog.csdn.net/litble/article/details/72804050
初涉莫比乌斯反演
http://blog.csdn.net/u013632138/article/details/52250567
莫比乌斯反演讲解
http://blog.csdn.net/Ripped/article/details/70263965
莫比乌斯反演详解
http://blog.csdn.net/hzj1054689699/article/details/51659994
莫比乌斯反演入门
http://blog.csdn.net/outer_form/article/details/50588307
莫比乌斯反演定理证明
https://zhuanlan.zhihu.com/p/36390998
Möbius inversion and Dirichlet convolution
Mobius Band可能是Mobius更著名的发现。
类似的还有Klein bottle。
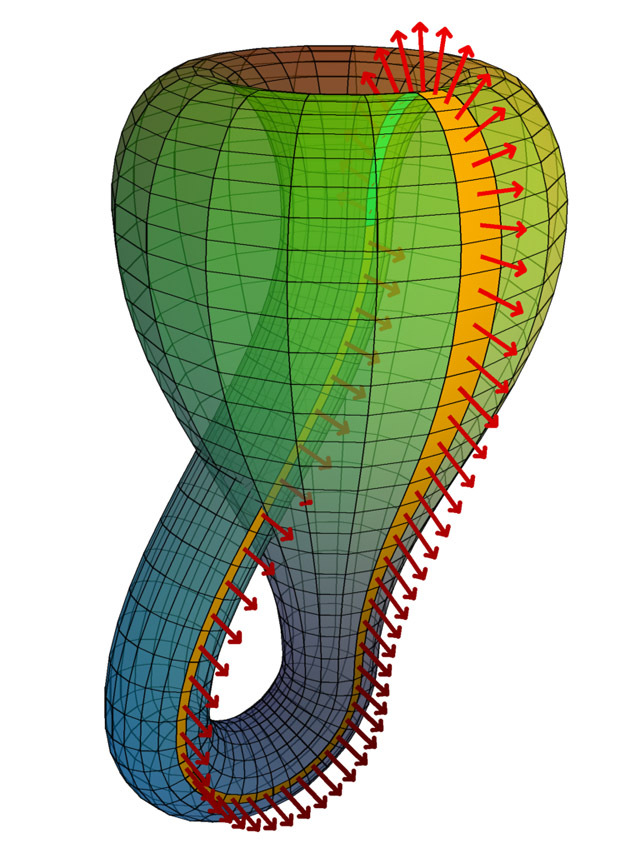
Felix Christian Klein,1849~1925,德国数学家。University of Bonn博士(1868),先后执教于Institute of Technology in Munich、Universities of Leipzig、Göttingen。
需要注意的是,Mobius Band一种2维变换,所以可以映射到3维空间,而Klein bottle本身是3维变换,只有在4维空间才能看到它的真面目,所以克莱因瓶实际上是造不出来的。
https://www.zhihu.com/question/23922861
克莱因瓶能否制造出来?
参考:
https://mp.weixin.qq.com/s/E-I_3C-3m0KTI1XjYaKWcA
陶哲轩挑战失败的百年数学问题,被两名在家隔离的数学家破解了。(任何简单闭合环路,是否总能在其上找到四个点形成一个任意长宽比矩形?)
Wavelet & Chirplet
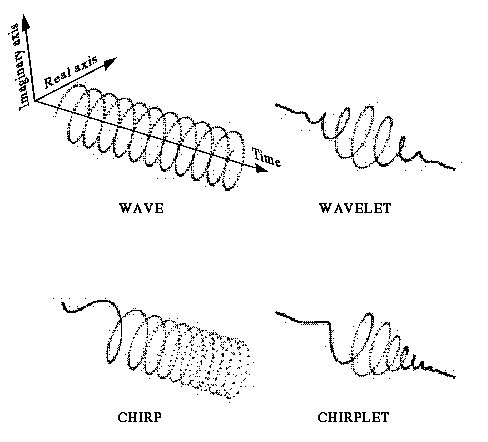
除了Fourier Transform之外,Wavelet Transform和Chirplet Transform也是信号处理中常见的变换。
| 名称 | 基函数 |
|---|---|
| Fourier Transform | 正弦波 |
| Wavelet Transform | 平方可积函数 |
| Chirplet Transform | 频率随时间变化的函数 |
Chirplet Transform在音频处理方面用的较多,因为人声和无线电通信不同,没有低频信号调制到高频信号的过程。
参考:
https://blog.csdn.net/sinat_26545113/article/details/78835038
什么是chirp信号
https://zhuanlan.zhihu.com/p/66189212
从傅立叶变换进阶到小波变换(一)
https://zhuanlan.zhihu.com/p/66246381
从傅立叶变换进阶到小波变换(二)
https://zhuanlan.zhihu.com/p/68323379
从傅立叶变换进阶到小波变换(三)
https://zhuanlan.zhihu.com/p/69956002
从傅立叶变换进阶到小波变换(四)
https://zhuanlan.zhihu.com/p/22450818
小波变换
Lanchester战争模型
第一次世界大战期间,英国工程师Lanchester针对战争问题建模,以预测战争的结果。
Frederick William Lanchester,1868~1946,被誉为英国三大最杰出的汽车工程师之一。英国皇家学会会员。
该模型包含了两个子模型:
Lanchester’s linear law:假设双方的装备能力相当,则单位时间内的损失,和战线的长度成正比,且双方损失的数量相等。这个模型主要适用于远程兵器威力有限的古代战争,古代战争以短兵相接的肉搏战为主。而肉搏战的特点就是一对一。
Lanchester’s square law:现代战争越来越立体化,因此是个多对多的模型。
首先,我们假设A军在战斗开始后的t时刻有\(x(t)\)人,B军在战斗开始后的t时刻有\(y(t)\)人,且每支军队的减员均由敌方攻击造成,减员速率与敌方人数成正比。忽略增员部队与非战斗减员,我们可以根据双方的减员速率列出如下的微分方程组:
\[\frac{\mathrm{d}x}{\mathrm{d}t}=-by\tag{1}\] \[\frac{\mathrm{d}y}{\mathrm{d}t}=-cx\tag{2}\]在上述微分方程组中,b与c分别代表B军与A军的单兵作战效率,即每个战士在单位时间内干掉的敌军数量。我们可以用这个量来代表士兵的“质量”或“效率”,显然这个量与军队的武器水平,指挥员的指挥水平与战士的单兵素质有关。
用公式2除以公式1,得:
\[\cfrac{\cfrac{\mathrm{d}y}{\mathrm{d}t}}{\cfrac{\mathrm{d}x}{\mathrm{d}t}}=\frac{-cx}{-by}\] \[\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{cx}{by}\] \[by\mathrm{d}y=cx\mathrm{d}x\]两边同时求t的定积分:
\[\int_{t_0}^t by(t)\mathrm{d}y(t)=\int_{t_0}^t cx(t)\mathrm{d}x(t)\] \[b\int_{y_0}^y y\mathrm{d}y=c\int_{x_0}^x x\mathrm{d}x\] \[by^2-by_0^2=cx^2-cx_0^2\] \[by^2-cx^2=by_0^2-cx_0^2=K\]我们可以由b,c,与双方初始人数\(y_0,x_0\)计算出K值。显然:
当K=0时,A、B平手。
当K>0时,B胜。
当K<0时,A胜。
Lanchester模型是一个连续模型,但实际战斗,尤其是海战,一般是离散模型,这时就要用到Salvo combat model了。
比如中途岛战役,美国在击沉日本3艘航母之后,遭到日本飞龙号的反击,损失了约克城号,直到第二波攻击,才最终将飞龙号击沉。
参考:
https://mp.weixin.qq.com/s/npprTz_GRgdv3BK7ff2grg
Lanchester战争模型:用可分离变量的微分方程占卜战事
https://scienceasdf.gitee.io/programming/2015/11/02/tank/
红警坦克作战效能模拟平台
数学杂谈

日心说这个东西,现在的人总觉得古人脑子怎么不开窍,老以自己为中心,而没有想到地球围绕太阳转。
其实日心说,古代就有。之所以不流行,是因为遇到了托勒密这个大牛,这哥们对球面几何和三角函数都研究的很深,发明了最早的三角函数表。
托勒密的著作中不但建立了地心说模型,而且还有数学推导。这也使得他的反对者,长期以来搞不定他。
就是哥白尼,其实也没有能翻案。真正搞定托勒密,要等到开普勒时代了。
参考:
https://mp.weixin.qq.com/s/jIlE6VDlgOgoIpUBiGzF5w
他(Claude Ptolemy)是被埋没了1300年的超级学霸,却凭一己之力,影响世界,改变人类文明!
https://www.zhihu.com/question/660377763
开普勒当时是如何计算出行星轨道是椭圆的呢?

您的打赏,是对我的鼓励
