math » 数学狂想曲（十七）——自适应滤波器, 三门问题, 平面几何
2021-04-23 :: 5498 Words自适应滤波器
《自适应滤波器原理（Adaptive Filter Theory）》，Simon Haykin著。
基本估计
三种基本的信息处理运算：
滤波（Filter）：利用\([0,t]\)的数据，来估计t时刻信息的运算过程。
平滑（Smoothing）：利用\([0,t]\)的数据，来估计\(t'(t'<t)\)时刻信息的运算过程。
预测（Prediction）：利用\([0,t]\)的数据，来估计\(t+\tau(\tau>0)\)时刻信息的运算过程。
可见，滤波和预测是实时运算，而平滑是非实时运算。
Optimal Wiener Filters
Norbert Wiener，1894～1964，美国数学家，控制论之父。18岁获得Harvard博士。MIT教授。
Wiener Filter主要用于平稳状态下的线性滤波。该滤波器在均方误差意义上是最优的。误差信号均方值相对于线性滤波器可调参数的曲线，称为误差性能曲面。该曲面的极小点即为Wiener solutions。
根据滤波器的记忆能力，可将线性滤波器分为Finite Impulse Response和Infinite Impulse Response，分别代表有限记忆和无限长但衰减的记忆。
FIR：
\[y(k)=\sum_{k=0}^M b_k x(n-k)\]IIR：
\[y(k)=\sum_{k=0}^N a_k y(n-k) + \sum_{k=0}^M b_k x(n-k)\]由于IIR的当前输出受到以前输出值的影响，所以它是有反馈的，或者说其输出值是递归的；相对应的，FIR就是无反馈、非递归的。
从Z域的角度看：
\(H(z)\)有分母的就是IIR，因为有自环，一个冲激响应会一直在系统里循环；
\(H(z)\)没有分母的就是FIR，因为没有自环，一个冲激响应不会在系统里一直循环。
在非平稳环境下，误差性能曲面随时间变化而变化，但只要输入数据的变化与算法学习率相比是慢的，则滤波器就能跟踪住。
参考：
https://blog.csdn.net/bluecol/article/details/46242355
图像去模糊（维纳滤波）
三门问题
https://www.zhihu.com/question/26709273/
蒙提霍尔问题（又称三门问题、山羊汽车问题）的正解是什么？
https://zhuanlan.zhihu.com/p/21461266
数学杂谈——“三门问题”：Monty Hall Problem
https://zhuanlan.zhihu.com/p/23338174
蒙提霍尔问题/三门问题（Monty Hall problem）
https://mp.weixin.qq.com/s/xHm4AjopGKSUE0-uAk5IHg
用概率论告诉你：直觉到底有多不靠谱。包括了三门问题和本福特定律。
Harmonic Number
调和级数：
\[H_n=\sum_{k=1}^n \frac{1}{k}\]这是一个增长极其缓慢（前一万亿项相加约为28），但却最终发散的级数。
欧拉给出了近似计算公式：
\[H_n \approx ln(n) + \gamma + \frac{1}{2n}\]这里的\(\gamma\)被称为Euler-Mascheroni Constant。
https://mathworld.wolfram.com/HarmonicNumber.html
Harmonic Number
https://baike.baidu.com/item/调和级数
调和级数
Lie Groups
《State estimation for Robotics: A Matrix Lie Group Approach》
Marius Sophus Lie，1842～1899，挪威数学家。University of Christiania博士（1871），University of Leipzig教授。当时德国的大学，一个系只有一个教授，所以这里的教授相当于现在的系主任或者院长。Lie接的是Felix Klein的班，后者跑到University of Göttingen当教授去了。
Galois建立群论后，一元n次方程的求解解决了，人们希望能继续前进，能够用群论求解牛顿的微分方程。
李发现，连续群是一个空间，每一个元素都可以用矩阵表示，由于连续，所以矩阵相当一个函数。正如一个抽象曲线（曲面）上的一个点，每个点的导数都具有特别的性质。
进一步，李发现矩阵（函数）的导数等于系数乘以它本身，这个系数具有特殊的性质，李将之命名为李代数。李群的问题便转为李代数的问题，因为一个元素的导数等于一个李代数乘以元素本身。
参考：
https://zhuanlan.zhihu.com/p/33156814
李群和李代数
https://zhuanlan.zhihu.com/p/76959511
李群和李代数（一）：刚体的三维运动
https://zhuanlan.zhihu.com/p/77576417
李群和李代数（二）：矩阵李群基础
https://zhuanlan.zhihu.com/p/80663767
李群和李代数（三）：优化基础
https://zhuanlan.zhihu.com/p/87438999
李群和李代数（四）：姿态估计小结
https://mp.weixin.qq.com/s/xGVvlVg6MxI5YjEF1giyWA
机器人状态估计中的简明李群理论(一)
https://mp.weixin.qq.com/s/7WebKui-so9YloZgovNsAg
机器人状态估计中的简明李群理论(二)
Sophus
Sophus是一个C++写的Lie Groups的库。显然，它得名自Marius Sophus Lie。
代码：
https://github.com/strasdat/Sophus
平面几何
共线向量定理
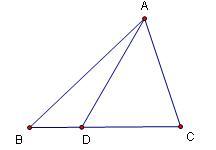
\(\triangle ABC\)中，点D在直线BC上的充要条件是:
\[\overrightarrow{AD}=\frac{\overline{DC}}{\overline{BC}}\cdot\overrightarrow{AB}+\frac{\overline{BD}}{\overline{BC}}\cdot\overrightarrow{AC}\]其中，\(\overrightarrow{AD}\)表示向量，\(\overline{DC}\)表示向量的数量。
Ceva’s Theorem
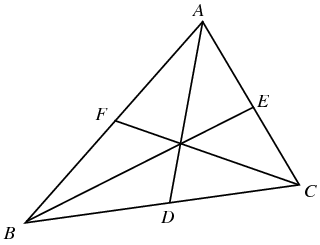
Giovanni Ceva，1647～1734，意大利数学家。Ceva’s Theorem是Ceva于1678年提出的。
Archimedes’ Theorem of the Broken Chord
阿基米德中点定理/阿基米德折弦定理：
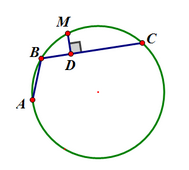
AB和BC是圆的两条弦（即ABC是圆的一条折弦），BC>AB，M是弧ABC的中点，则从M向BC所作垂线之垂足D是折弦ABC的中点，即CD=AB+BD。
定义：从圆周上任一点出发的两条弦，所组成的折线，我们称之为该图的一条折弦。
拓扑学
《Topopogy Without Tears》，University of New South Wales的Sidney A. Morris著。
该书的中文版：
http://www.topologywithouttears.net/topbookchinese.pdf
参考：
https://mp.weixin.qq.com/s/QmDCFY0SP3cl71HvwvthJQ
如果高斯没有故意“坑”黎曼，估计这门神奇的学科就不会出现了……（拓扑学（Topology）是一门研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。）
https://mp.weixin.qq.com/s/H6QV5L-Ewdb1NkMKZrNK9w
一杯咖啡背后的拓扑
https://mp.weixin.qq.com/s/zoMJpYQeAAt6GmjPDx863Q
这个“橡皮泥几何”，竟然解决了城中村难题！实在是太牛了！
数学杂谈
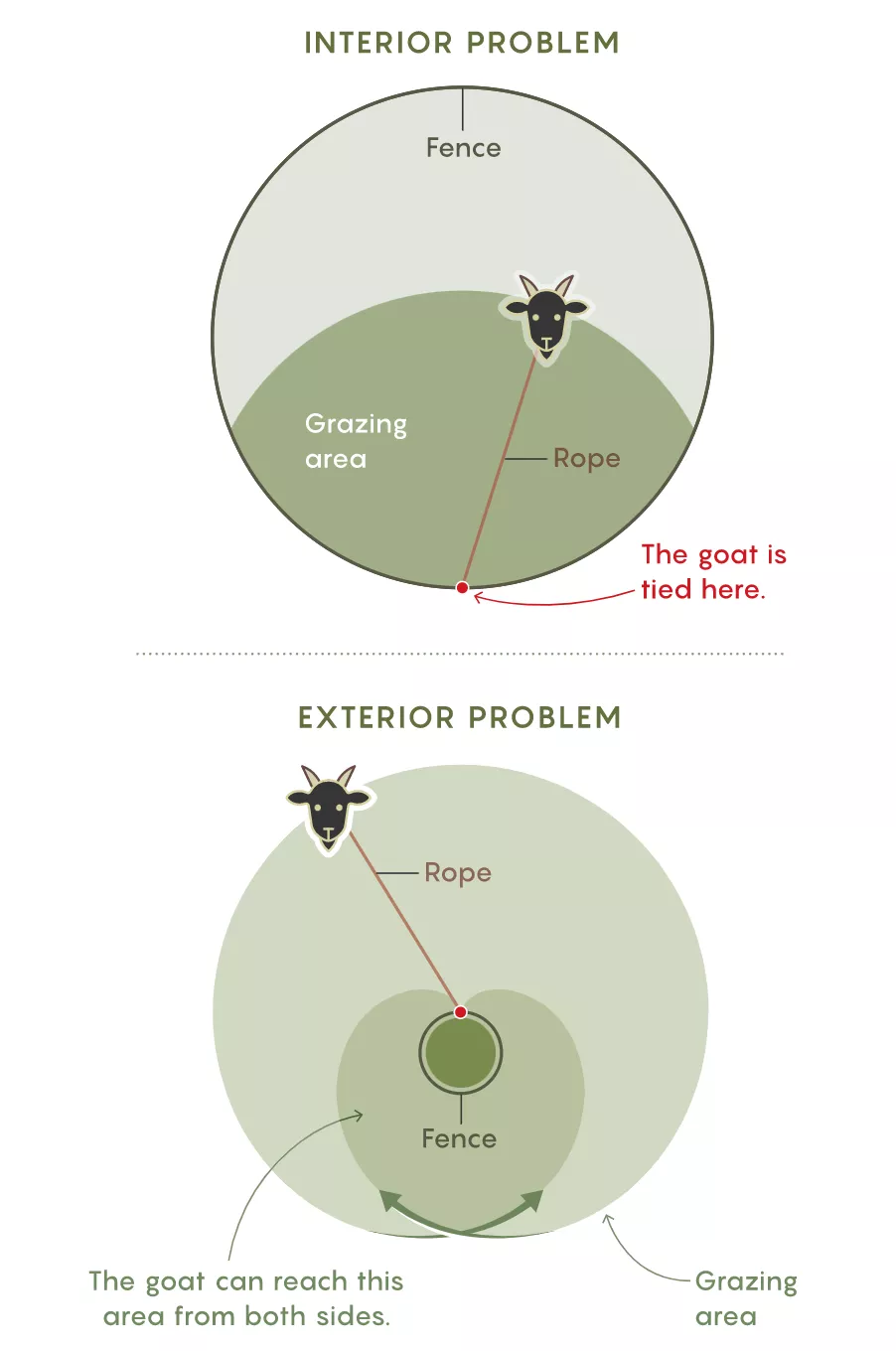
山羊吃草问题有两种形式。内部问题是给出吃草面积求绳长，外部问题是给出绳长和篱笆周长求吃草面积（绳长等于篱笆周长）
https://mp.weixin.qq.com/s/OCTifPIZHVjYWjuxyQQWbA
诞生272年后，这个看似简单的数学问题终求得闭式解（山羊问题）
https://mp.weixin.qq.com/s/ydYVWnsEQ5QFLWmiDxeSTg
两圆重叠问题你会求解吗？
从研究数学和物理的角度，牛顿的《自然哲学的数学原理》其实并不适合今天的读者阅读。
比如牛顿的第二定律和引力定律，今天主要是以代数的方式求解。即使要运用到真实空间的运动上，也是以解析几何的形式出现。
但牛顿时代，解析几何才刚出现，更早的开普勒时代，还没有这东西。当时的科学家采用什么方法解决运动问题呢？
答案是：古希腊流传下来的几何方法。代表作：《几何原本》、《阿基米德全集》和《圆锥曲线论》。尤其阿波罗尼奥斯的《圆锥曲线论》堪称希腊古典时代的巅峰之作。
微积分不是牛顿的发明，他既不是首创者，也非终结者，但却是一个重要的里程碑人物。
微积分的思想首先来源于古希腊哲学家芝诺提出的芝诺悖论，到欧几里得手上，总结得到“穷竭法”，并提出了左右极限的夹逼准则。事实上，高中阶段的极限思想的结论，绝大多数在希腊古典时代已经被得出。
阿基米德应用穷竭法得到了球体积和球表面积公式。
阿波罗尼奥斯更在解析几何出现前1800年，就求解了几乎所有的圆锥曲线性质。《圆锥曲线论》后面几卷的一些命题，难度远超高中奥数题。
所以今天的读者如果没有那三本古书的基础，实际上是很难看懂《自然哲学的数学原理》的。
PS：1.《几何原本》不代表欧几里得的最高水平，那是欧几里得写给学生的教材。他的最高成就体现在《阿基米德全集》和《圆锥曲线论》中。后两书的作者都曾在亚历山大图书馆留学，受到过欧几里得及其门徒的教导，而且他们在书中也提到，某些命题归功于欧几里得。
2.解析几何中的坐标轴是阿波罗尼奥斯的发明，只是当时代数不发达，不然解析几何的发明者轮不到笛卡尔。阿波罗尼奥斯的天分之高，比笛卡尔强多了。
3.莱布尼茨说过，读过阿基米德和阿波罗尼奥斯的书之后，就知道世上并没有什么更天才的人物了。
Introspective Neural Networks
http://www.cnblogs.com/cyjb/p/UnionFindSets.html
并查集（Union-find Sets）
高斯背景
laurent series
方差分析(Analysis of Variance，简称ANOVA)
Partial Least Squares Discriminant Analysis
Wavenumber
当我在32岁成为哈佛大学终身教授的时候，终于有时间学习如何运算了——是如坐针毡地和一群年龄仅仅是我的一半多点的大学小鬼们一起上课。他们中的一些人还在上我执教的进化生物学。我将自尊搁置一边，来学习微积分。当在追赶中学习时，成绩拿C都费劲。—By Edward Osborne Wilson
Edward Osborne Wilson，1929年生，美国生物学家，以研究蚂蚁著称，被称为生物社会学之父。同时也是一名杰出的科普作家，两获Pulitzer Prize。
Yau Shing-Tung=姚兴腾
6世纪末，弗朗索瓦·韦达（Francois Viete）的出现，强化了法国人破解密码的技能。
韦达特别以破解西班牙的密码为乐。西班牙的密码专家，似乎比欧洲其他地方的对手天真。当他们发现法国人可以看透他们的信息时，竞不愿正视这件事实。西班牙国王菲利普二世甚至向梵蒂冈陈情，宣称韦达之所以能破解西班牙密码的唯一解释是：他是“与撒旦结盟的魔王”。菲利普诉请枢机法庭审判韦达的恶魔勾当。
教皇深知自己的密码分析家多年来也一向能破解西班牙的密码，于是驳回他的陈情。这则新闻很快就传到各国专家的耳朵里，西班牙的密码专家顿时成为全欧的笑柄。
https://mp.weixin.qq.com/s/SlbWkTrO3UlWd15jrKYvdg
史上最强律师，用代数暴力破解军事密码，无情吊打荷兰数学家，被誉为“代数学之父”（弗朗索瓦·韦达）
https://www.sohu.com/a/284210653_161479
日本大学生把数学“玩坏”：为了画好一只乳房，也是拼了！
https://www.zhihu.com/question/20866833
为什么正多面体只有5种？
https://mp.weixin.qq.com/s/qfbfzToypKTxh7CxJ0ifHw
正十二面体的一个最基本谜题被破解了
您的打赏，是对我的鼓励
