• 阴影面积
• 勾股定理
• Menelaus’ Theorem

阴影面积

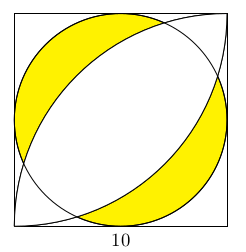
题如上图，已知正方形边长为10，求阴影面积。

解：

旋转图形建立坐标系如下图：

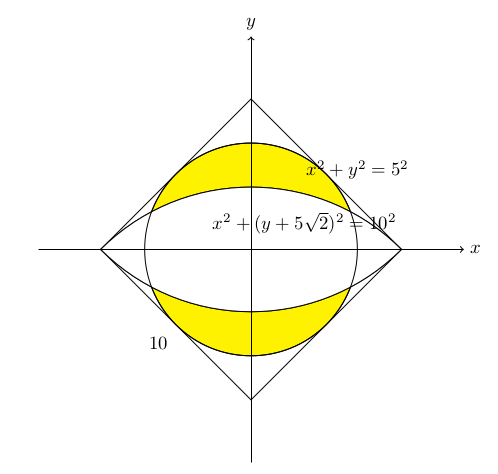
阴影部分上下曲边公式如下：

\[\begin{cases} x^2+y^2=5^2 \\ x^2+(y+5\sqrt{2})^2=10^2 \end{cases}\]

求解交点坐标：

\[(y+5\sqrt{2})^2-y^2=75 \to 10\sqrt{2}y+50=75\] \[\begin{cases} y=\frac{5\sqrt{2}}{4} \\ x=\sqrt{\frac{175}{8}} \end{cases}\]

用积分法求解阴影面积：

\[\begin{align} \frac{S}{4} & =\int_0^{\sqrt{\frac{175}{8}}}\sqrt{(5^2-x^2)}-(\sqrt{(10^2-x^2)}-5\sqrt{2})\mathrm{d}x \\ & = \int_0^{\sqrt{\frac{175}{8}}}\sqrt{(5^2-x^2)}\mathrm{d}x - \int_0^{\sqrt{\frac{175}{8}}}\sqrt{(10^2-x^2)}\mathrm{d}x + 5\sqrt{2} \cdot \sqrt{\frac{175}{8}} \end{align}\]

查常用积分表，可得：

\[\int \sqrt{a^2 - x^2}\mathrm{d}{x} = \frac12 \left(x\sqrt{a^2 - x^2} + a^2\arcsin\frac xa\right) + C\] \[\begin{align} \frac{S}{4} & =\left[\frac{25}{16}\sqrt{7} + \frac{25}{2}\arcsin(\frac{\sqrt{\frac{7}{2}}}{2})\right] - \left[\frac{125}{16}\sqrt{7} + 50\arcsin(\frac{\sqrt{\frac{7}{2}}}{4})\right] + \frac{25}{2}\sqrt{7} \\ & = \frac{25}{4}\sqrt{7} + \frac{25}{2}\arcsin(\frac{\sqrt{\frac{7}{2}}}{2}) - 50\arcsin(\frac{\sqrt{\frac{7}{2}}}{4}) \end{align}\] \[S=25\sqrt{7} + 50\arcsin(\frac{\sqrt{\frac{7}{2}}}{2}) - 200\arcsin(\frac{\sqrt{\frac{7}{2}}}{4})\approx 29.27625\]

本答案使用Tikz绘图，相关文件地址：

https://github.com/antkillerfarm/antkillerfarm_crazy/blob/master/helloworld/tikz/gnuplot/p1.tex

参考：

https://www.zhihu.com/question/60697114

网传无锡小升初题，求阴影面积

http://wuli.wiki//online/ITable.html

积分表

http://wuli.wiki//online/

小时物理百科

---

https://zhuanlan.zhihu.com/p/699224923

交圆公式

勾股定理

勾股定理在西方被称为Pythagorean theorem。它的命题本身并不复杂，也就是初中几何的内容，但是内涵非常丰富。即使大学数学也未必能穷尽其中的奥妙。这里仅罗列一二。

Pythagoras of Samos，约570 BC～约495 BC，古希腊哲学家。那时候的哲学家比现在牛多了，通常都是兼通数门学科的宗师级人物。

使用勾股定理定义的距离，也就是通常的Euclidean Distance。之所以用Euclid命名是因为：勾股定理实际上和Euclid几何的平行公理是等价的。

空间拓扑结构对于定理的影响不仅于此。以下就是欧氏空间的一些有意思的等价结论：

Euclidean Distance（2范数） => 最小二乘法 => 正态分布

由于GMM隐含使用了Euclidean Distance，所以K-Means聚类可以采用任意距离，但GMM只能采用欧氏距离。

同理，为什么多数误差都符合正态分布？因为我们生活的空间是Euclidean space，多数的物理定律都是各向同性的，也只有Euclidean space才满足这种对称性。

不对称的空间也有，例如：

Manhattan Distance（1范数） => 拉普拉斯分布

不满足勾股定理的几何，也就是非欧几何。但实际上，Euclid对于其中的特例——球面几何，也有一定的研究。比如，著名的“球面三角形相似必全等”，就是他发现的。

参考：

https://mp.weixin.qq.com/s/Z3WVdFwDGqikWcLnM0zTOQ

颠覆认知！关于\(c^2=a^2+b^2\)，你不知道的N个事实

https://mp.weixin.qq.com/s/h_BjRGiNFV0V511RUumR0w

L1, L2 范数以及高斯，拉普拉斯分布

Menelaus’ Theorem

\[AD\cdot BE\cdot CF=BD\cdot CE\cdot AF\]

Menelaus of Alexandria，公元70～140年，古希腊数学家、天文学家。青年时期求学于Alexandria，后定居于Rome。他第一个认识到曲面上的测地线（geodesics）可以类比于平面上的直线。

不要和荷马史诗中，美女Helen的前老公，那个也叫Menelaus的国王搞混了。

上图是这个定理的平面几何版本，相关的证明过程，网上已经很多了，这里不再赘述。

让我感兴趣的实际上是以下球面几何版本：

\[\frac{Crd \; arc \; 2BZ}{Crd \; arc \; 2AB} = \frac{Crd \; arc 2HZ}{Crd \; arc 2H \Theta} \cdot \frac{Crd \; arc \; 2E \Theta}{Crd \; arc \; 2AE}\]

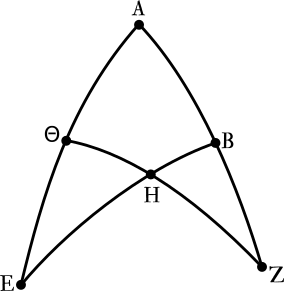
最早的三角术没有使用\(\sin\)之类的现代符号和现代定义，而是用两倍的弧长对应的弦长来定义正弦。

证明过程：

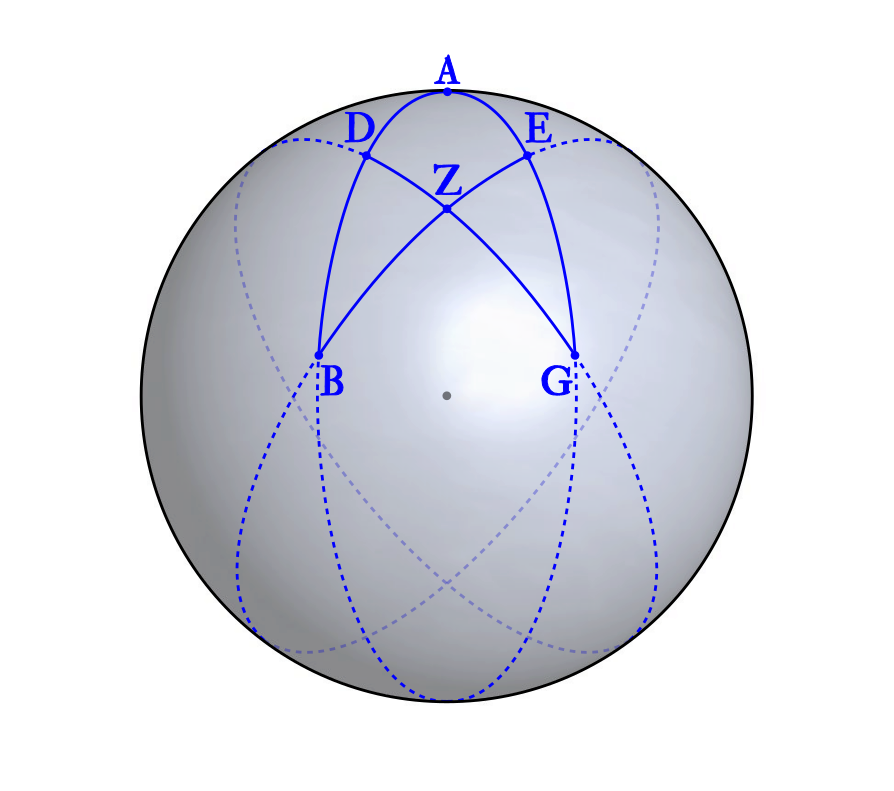
添加辅助线：

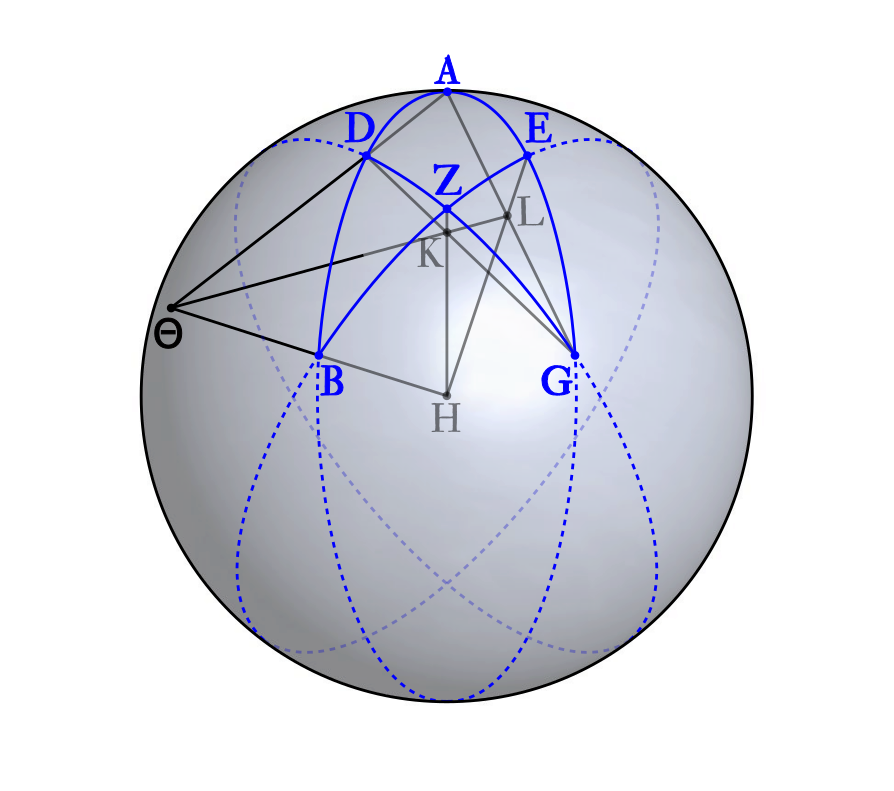
去掉无关的线之后，得到一个平面版本：

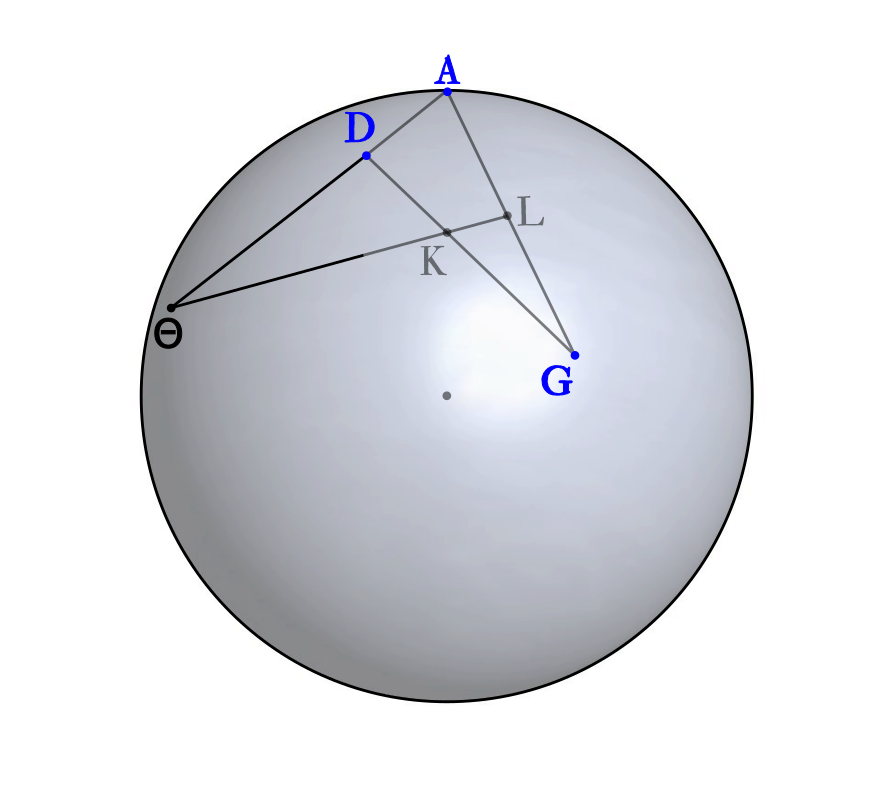
弦的比例关系确定了，对应圆弧的比例也就定了：

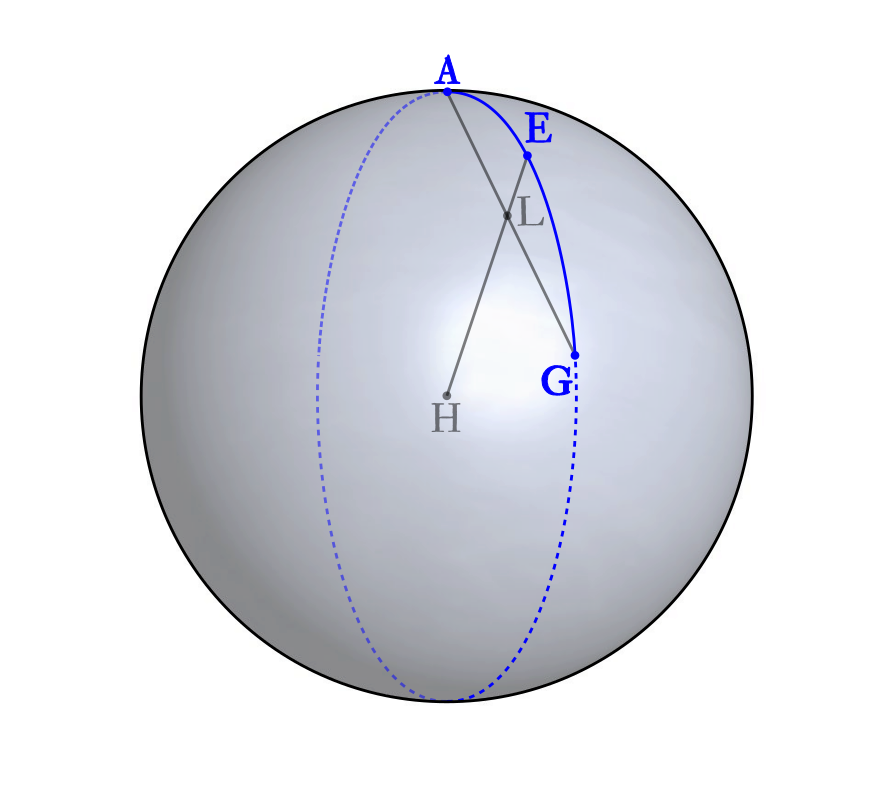
Menelaus’ theorem现存最早的记录是Menelaus的著作《Spherics》。书中将平面版本的Menelaus’ theorem作为引理引入，并将之推广到球面三角形。按照当时的写作习惯，引理一般记述的是前人的成果，因此，Menelaus’ theorem的平面三角版本的发现者应该另有其人，只有球面三角版本才是他的原创。

Menelaus的贡献不止于此。还有下图：

\[\frac{\sin AD}{\sin DC} \cdot \frac{\sin BC}{\sin AB} = \frac{\sin A'D'}{\sin D'C'} \cdot \frac{\sin B'C'}{\sin A'B'}\]

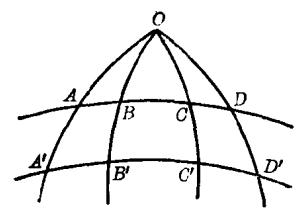
当然这个也是作为引理引入的，多半也是前人的发现。这实际上就是后世的射影几何学中的cross ratio。

从这里还可以得到一个学习曲面几何的小技巧或者说是直觉：圆弧=平面版本+正弦，双曲弧=平面版本+双曲正切。

此外还有球面三角形全等的AAA条件。这也是唯一的一个三角形全等条件中，球面三角形和平面三角形不同的地方。

当然了，考虑到这个条件和欧式几何平行公理的密切联系，那么这个结论可能仍然还是前人的发现，而发现者极大可能就是Euclid本人。

和人们通常的想法不同，三角术从一开始就是球面三角学，因为它的几个最初的奠基人（Hipparchus、Menelaus、Ptolemy）都是天文学家。。。平面三角学反而是很后来的事情了。。。大地测量对于Ptolemy这样的神兽来说，显然太low了。。。

类似的，Euclid的真正本事，其实并不在《几何原本》中，而是在稍后时代相关数学家的记述中。一般认为几何原本只是Euclid给自己弟子编写的入门书籍，完全显不出Euclid的真正水平。

最后，再稍微从现代的角度解释一下，为什么弦的比例关系确定了，对应圆弧的比例也就定了。以及这个比例为什么是正弦。

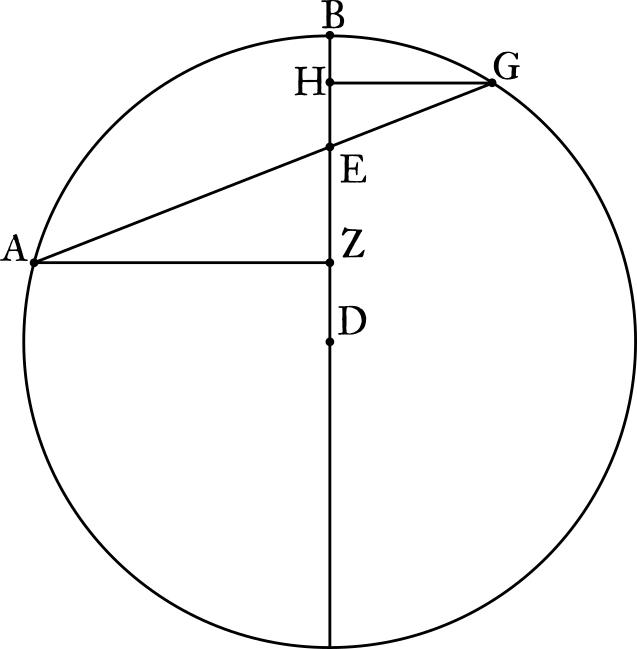
假设上图是个单位圆，那么从弧度制的角度来看，\(arc AB\)实际上就等价于\(\angle{ADB}\)。

所以：

\[AZ = \sin (\angle{ADB}) = \sin (arc AB)\]

但是从正弦定义的角度出发，要求AZ垂直于BD，这在实际的应用中是非常不方便的。好在根据相似三角形的性质，我们有以下推论：

\[\frac{AZ}{GH} = \frac{AE}{GE}\]

所以：

\[\frac{AE}{GE} = \frac{\sin (arc AB)}{\sin (arc GB)}\]

从上图不难看出，Menelaus’ Theorem的平面版本的证明或者不需要三角术，但球面版本是一定要三角术的。

这也可以从另一个角度解释平面三角学为何出现的晚。大地测量界并非没有高手，比如有小Archimedes之称的Heron，其咖位尚在Ptolemy之上。然而平面几何的那些问题，对于Heron来说过于简单，不值得发明新的工具。而普通的大地测量员，显然又没有能力发明三角术这样的工具。

Heron算的上是上古神兽中的异类了。他是那个时代少有的代数和几何都很溜，证明题和数值计算全精通，同时还点了物理、机械方面的技能树的全能骑士。可惜的是，在他之前已经有了全能骑士Archimedes，而且Archimedes在各方面的贡献都比他略胜半筹。所以Heron也就只能被称为小Archimedes了。

如果给上古神兽排个名的话，Archimedes肯定在前三名，Heron在5～10名中找个位置也不难，Ptolemy虽然顶着天文学之父的名头，但无奈高手太多，能不能进前10，就见仁见智了。

这里索性给一下我自己的上古神兽排名。

第一档：Euclid、Archimedes。

第二档：

Pythagoras，勾股定理。Pythagoras学派是古希腊最有数学传统的学派。

Apollonius，古希腊几何最高成就者，《圆锥曲线论》将圆锥曲线的性质网罗殆尽，几乎使后人没有插足的余地。

第三档：

Thales，古希腊七贤之一。三角形全等和相似三角形。贡献了《几何原本》差不多一卷的内容。

Eudoxus。这个名字虽然现在不太出名，但在当时是公认的天下第一大数学家，Euclid也没有他的名气大。直到妖孽一般的Archimedes横空出世，才把天下第一的名头抢下来。《几何原本》有差不多五卷的内容都是他的成果。从某种意义上来说，他才是《几何原本》的真作者。

Heron。

第四档：

Eratosthenes，地理学之父，亚历山大里亚图书馆馆长。

Hipparchus、Ptolemy，这两人都有天文学之父的称号。前者有开创之功，后者号称天文学的集大成者。

Diophantus，代数之父。

第五档：

Pappus，这个人本身的水平一般。但是他的书里收录了很多前人的成果。正是通过他，我们才知道之前的那些上古神兽有多么厉害。他也是古希腊最后一个知名的数学家了。

番外篇：

Plato，虽然他的学院立了个“不懂几何者，不得入内!”的牌子，但是他本人在数学上真的只是个菜鸡。

Aristotle，比他的老师Plato略强一些，贡献了逻辑推理，以及著名的反证法，此外还有几个小的数学命题。但在数学上，还达不到神兽的级别。

尽管有这些缺点，但必须承认的是，这两人是当时科学界的中心。他们的老师、同学、朋友、同事、学生中，一大把的数学家。。。

参考：

https://zhuanlan.zhihu.com/p/27355643

三角术

http://jonvoisey.net/blog/2018/05/almagest-index/

Almagest(天文学大成, Ptolemy著)

https://www.math.csi.cuny.edu/~ikofman/Polking/The%20Geometry%20of%20the%20Sphere.html

The Geometry of the Sphere

https://mathstat.slu.edu/escher/index.php/Spherical_Geometry

Spherical Geometry

https://zhuanlan.zhihu.com/p/97346034

球面三角学基础