math » 数学狂想曲（十）——熵
2018-09-27 :: 5503 Words熵
经典热力学定义（续）
由Carnot’s theorem可以容易的得到如下结论：
1.冷热温度是热机效率的关键因素。但是低温热源降温是件很麻烦的事，需要设计基于Carnot逆循环的热机。这实际上就是现代空调的原理。
2.提高高温热源温度。比如内燃机就比蒸汽机热效高。
3.Carnot逆循环还表明，没有外界做功，低温热源不可能降温。这实际上揭示了热的不可逆特性，也就是热力学第二定律。
必须指出的是，Carnot时代，科学界主流的理论还是热质说。虽然当今课本介绍Carnot’s theorem时，一般基于热力学第二定律进行讲解，但后者的发现实际上是30年之后的事了。
到了1850年代，Rudolf Clausius深入研究Carnot cycle之后，发现如果用负号表示放热的话，公式9可改写为：
\[\frac{Q_1}{T_1}+\frac{Q_2}{T_2}=0\tag{11}\]这表明Carnot cycle中的路径积分：
\[\oint \frac{Q}{T} = 0\]然而Carnot cycle是理想状况，真实热机不可能达到。因此：
\[W<\left(1-\frac{T_C}{T_H}\right)Q_H\tag{12}\] \[Q_H-Q_C<\left(1-\frac{T_C}{T_H}\right)Q_H\]即：
\[Q_C>\frac{T_C}{T_H}Q_H\]也就是：
\[\oint \frac{Q}{T} \le 0\tag{13}\]Clausius意识到
\[dS = \frac{Q}{T}\tag{14}\]是一个很重要的物理量，于是将之命名为Entropy。En表示energy，tropy是希腊文中transformation的意思。当这个颇有来历的名称被1923年到南京讲学的普朗克介绍给中国物理学家时，胡刚复教授在翻译时灵机一动，创造了一个新词汇“熵”。
Rudolf Julius Emanuel Clausius，1822～1888，德国物理学家和数学家。University of Halle博士（1847）+ETH Zürich教授。经典热力学的集大成者。普法战争期间，上战场获得了一枚铁十字勋章。
胡刚复，1892～1966，物理学家。哈佛大学博士（1918），历任南京大学、上海交通大学、浙江大学、南开大学教授。他和兄弟姐妹胡敦复、胡明复、胡范若、胡芷华等创办了上海大同大学，是上海乃至全国私立大学中的翘楚，素有“北有南开、南有大同”之说。
从公式13可以看出，如果没有外界能量注入，热机是无法完成循环的，但由热力学第一定律可知，系统的能量总量是不变的，因此这意味着系统的一部分能量成为了无法利用的能量，而这部分能量正好可以用Entropy进行度量。
参考：
http://galileo.phys.virginia.edu/classes/152.mf1i.spring02/CarnotEngine.htm
Heat Engines: the Carnot Cycle
统计热力学定义
Entropy的统计热力学定义，相对就比较复杂了。这里仅列出推导的要点，不细讲了。
首先是两个假设：
1.统计物理量的加和性。（刘维尔定理）
2.概率分布的乘积性。（不相关变量的概率分布公式）
设系统有两部分，其熵为\(S_1,S_2\)，其概率分布为\(\Omega_1,\Omega_2\)，则根据上述假设可得：
\[S=S_1+S_2\] \[\Omega=\Omega_1\times \Omega_2\]令\(S=f(\Omega)\)，则：
\[S_1=f(\Omega_1),S_2=f(\Omega_2),S=f(\Omega_1)+f(\Omega_1)=f(\Omega_1\times \Omega_2)\] \[\begin{cases} \frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega_1} = \frac{\mathrm{d}f(\Omega_1\times\Omega_2)}{\mathrm{d}(\Omega_1\times\Omega_2)}\mathrm{d}\Omega_2 \\ \frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega_2} = \frac{\mathrm{d}f(\Omega_1\times\Omega_2)}{\mathrm{d}(\Omega_1\times\Omega_2)}\mathrm{d}\Omega_1 \\ \end{cases} \Rightarrow \begin{cases} \Omega_1\frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega_1} = \frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega}\Omega \\ \Omega_2\frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega_2} = \frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega}\Omega \\ \end{cases}\] \[\Omega_1\frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega_1} =\Omega_2\frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega_2}=\frac{\mathrm{d}f(\Omega)}{\mathrm{d}\Omega}\Omega = K\] \[\mathrm{d}f(\Omega)=K\frac{\mathrm{d}\Omega}{\Omega}\Rightarrow f(\Omega) = K\ln \Omega + C\]根据热力学第三定律，使用绝对零度作为原点，则：
\[S=K\ln \Omega\]上式就是Boltzmann’s entropy formula。这里隐含的另一个假设是：分子随机运动没有偏好性，即各状态的概率相等。
如果状态概率不等的话，则：
\[S = K \cdot E[\ln \Omega] = K \sum \Omega_i \ln \Omega_i\]上式被称作Gibbs entropy。
参考：
https://wenku.baidu.com/view/a90518a37c1cfad6185fa746.html
热力学中的熵
信息熵
信息熵和热力学熵的假设相同，因此有类似结论不足为奇，毕竟数学上都是同一个微分方程。
信息熵：编码方案完美时，最短平均编码长度的是多少。
交叉熵：编码方案不一定完美时（由于对概率分布的估计不一定正确），平均编码长度的是多少。平均编码长度=最短平均编码长度+一个增量
\[H(p, q) = -\sum_x p(x)\, \log q(x)\]相对熵：编码方案不一定完美时，平均编码长度相对于最小值的增加值。（即上面那个增量）
\[D_{\mathrm{KL}}(P\|Q) = - \sum_i P(i) \, \log\frac{Q(i)}{P(i)}\]参考：
https://www.zhihu.com/question/41252833
如何通俗的解释交叉熵与相对熵?
https://zhuanlan.zhihu.com/p/74075915
交叉熵、相对熵（KL散度）、JS散度和Wasserstein距离（推土机距离）
https://mp.weixin.qq.com/s/sglAI17L5NvZLvPg1P2ZSA
熵、交叉熵和KL散度的基本概念和交叉熵损失函数的通俗介绍
https://mp.weixin.qq.com/s/V8yeWoVM_HU1OnhgXOk6Vg
听说你还不知道条件熵是什么?
http://blog.csdn.net/luo123n/article/details/48574123
PMI（Pointwise Mutual Information）
Landauer’s Erasure Principle
在量子力学中，如同电荷、质量、时间有最小单位一样，热力学熵也有最小单位。Landauer’s Erasure Principle指出这个单位为\(K_B\ln(2)\)，其中\(K_B\)为玻尔兹曼常数。
Rolf Landauer，1927～1999，美国物理学家。出身于一个德国的犹太人家庭，1938年为躲避纳粹，全家移民美国。Harvard University本科（1945）+博士（1950）。IBM研究员。美国科学院、美国工程院院士。
需要指出的是：Landauer原理中虽有“信息”一词，但仍是物理学的概念，对应了物质/能量的转移。而信息熵是数学概念，对应的是抽象的对象。因此，前者的公式中还有一个\(K_B\)的存在。
参考：
https://mp.weixin.qq.com/s/Gmfu9iLC71XmfQ5qyraIpQ
信息的物理性：从麦克斯韦妖到兰道尔擦除
https://mp.weixin.qq.com/s/vlhgdxjVJaiD6VbX1u3how
新·麦克斯韦妖
https://mp.weixin.qq.com/s/G-PCyPVqoH77-4Gt_BhS8Q
一个经典热力学思想实验的量子版本（吉布斯佯谬）
焓
焓（hán，enthalpy）是一个和熵经常一起出现的概念。由于和信息论关系不大，这里仅作简要通俗的介绍，而非严格定义。
上面提到的热力学过程，只涉及气体的PVT变换，气体本身的其他状态并没有改变。而实际情况要复杂的多，比如气体会发生化学反应，也会发生相变（变成液态/固态），而这些变化本身，会吸收/释放热量，这时系统的内能就不再守恒了。焓就是用来度量这种变换的。
例如：
对于等温下的化学反应，若反应吸热，产物的焓高于反应物的焓；若反应放热，产物的焓应低于反应物的焓。
类似“焓”这样生造出的汉字还有：
㶲，yòng，Exergy，可以全部转换为任何其他能量形式的那部分能量。
㷻，wú，Anergy，不能够转化和利用的能量。
朗肯循环
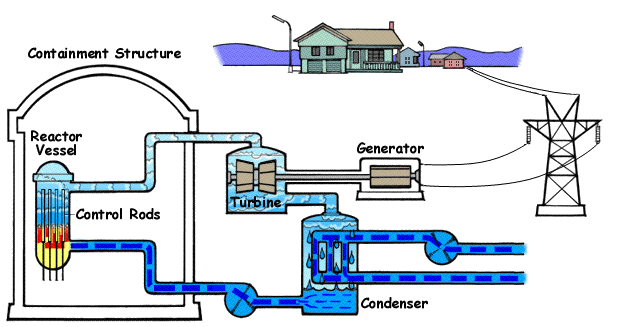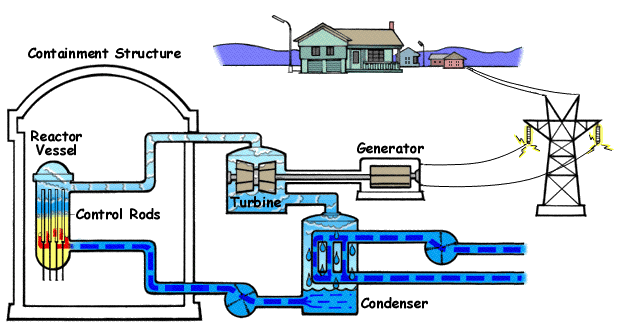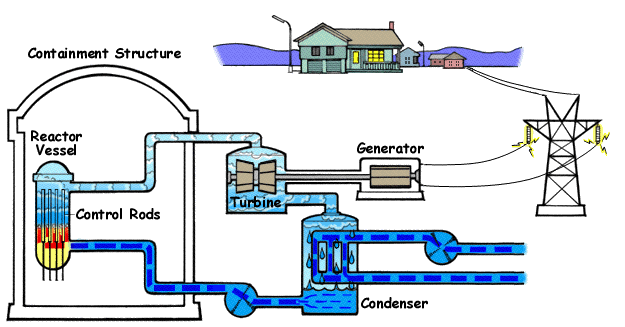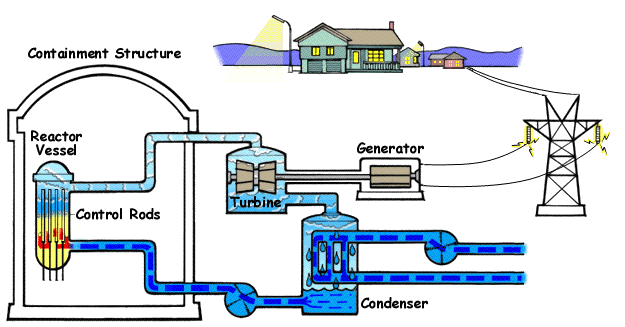
上图是核电站的原理结构图。可以看到，其中有一个冷却蒸汽的过程。
好容易被加热的蒸汽，为什么要冷却呢？
术语：释放出热势能的蒸汽从汽轮机下部的排汽口排出，被称为乏汽。
单纯的热蒸汽膨胀做功，是可以将热能完全转换为机械能的。然而，如果没有循环的话，这就成了一次性的买卖。而一个能够循环做功的热机，才是有实际用处的。这也是卡诺和朗肯为什么都要研究循环的原因。
乏汽的温度和蒸汽差不多，但气压却低的多，如果不加压的话，根本进不了锅炉加热。然而，压缩空气是一个耗费机械能的过程，由卡诺循环可知，它耗费的能量要大于蒸汽对汽轮机做的功，两者的差值就是所谓的熵。
而乏汽冷却之后变成了水，由于液体的不可压缩特性，它可以很方便的被压入锅炉，从而进入下一轮的循环。
朗肯循环就是用来研究以水为热机工质的循环的。这中间由于水发生了相变，因此是一个焓变过程。
和卡诺循环与热力学第二定律等价不同，朗肯循环的损耗并无定数，使用更优良的工质（比如低沸点有机物）可以提升热机的效率。
William John Macquorn Rankine，1820~1872，英国科学家。University of Edinburgh肄业（读了两年，家里没钱了）。University of Glasgow教授。
https://www.zhihu.com/question/26163433
为什么不能将乏汽直接送入锅炉，而要经过冷却后再送入锅炉？效率不是下降了吗？
数学杂谈
《素数之恋》这本书不错，黎曼猜想的最佳科普读本。
Sir Michael Francis Atiyah，1929年生，英国籍黎巴嫩裔数学家。剑桥大学博士（1955），英国皇家学会会长（1990～1995），获得过Fields Medal(1966)和Abel Prize(2004)。
Atiyah的高中在埃及读的（1941～1945），当时欧洲很多人为了躲避战乱，逃到了那里。
2019.1.11 Atiyah去世。
有种素数叫做“工业级素数（Industrial-grade primes）”，定义是没有经过严格数学证明、但是通过了“可能素数判定法”（比如米勒-拉宾判定法）的整数。用这种方法判定大整数是否是素数不是完全准确，但速度非常快，而且不会漏掉任何素数。RSA加密法所需的大素数生成方式就很明显了：随机生成大整数，如果判断这个数可能是素数，再用精确但速度慢的素数判定法来判断这个数是否真的是素数。
https://www.zhihu.com/question/54779059
RSA生成公私钥时质数是怎么选的？
https://mp.weixin.qq.com/s/zozViMoimcL6nJvyBnTQtQ
八岁小孩眼里的欧拉公式
这里讲的是拓扑学中的欧拉公式：V−E+R=2，然而成年人的世界里没有Easy这个词，V−E+R会不会等于其他数呢？于是就有了Euler characteristic。
您的打赏，是对我的鼓励
