math » 数学狂想曲（九）——随机过程, Bézier curve
2018-08-01 :: 6191 Words核弹当量问题（续）
https://futureoflife.org/background/us-nuclear-targets/
美国核弹目标清单（1959年）
https://nuclearsecrecy.com/nukemap/
一个核弹效果的评估网站
https://nuclearsecrecy.com/missilemap/
上述网站还有一个评估导弹的网页
https://www.zhihu.com/question/36188584
“大伊万”到底有多强？
https://baijiahao.baidu.com/s?id=1672436291069334638
纳粹德国为什么没有造出原子弹？就因为这个醉汉（醉汉回家问题）
随机过程
随机变量序列的收敛性
弱收敛：\(F_n(x)\xrightarrow{W}F(x)\)
依分布收敛：\(X_n\xrightarrow{L}X\)
依概率收敛：\(X_n\xrightarrow{P}X\)
r阶收敛：\(X_n\xrightarrow{r}X\)
几乎处处收敛（almost everywhere convergent）：\(X_n\xrightarrow{a.e.}X\) or \(X_n\xrightarrow{a.s.}X\)
一致收敛（uniform convergence）：\(X_n\xrightarrow{u.c.}X\)
以上概念实际上都是测度论的内容。具体到这里，弱收敛针对分布函数F，而其他收敛针对随机变量X。
收敛严格性：
\[X_n\xrightarrow{P}X \supseteq X_n\xrightarrow{L}X\] \[X_n\xrightarrow{r}X \supseteq X_n\xrightarrow{P}X\] \[X_n\xrightarrow{a.s.}X \supseteq X_n\xrightarrow{P}X\]大数定律：
依概率收敛->弱大数定律
几乎处处收敛->强大数定律
随机过程常用公式或符号
| 名称 | 公式或符号 |
|---|---|
| 期望 | \(EX=\int_{-\infty}^{+\infty}x\mathrm{d}F(x)\)，若存在密度函数则\(EX=\int_{-\infty}^{+\infty}xf(x)\mathrm{d}x\) |
| 方差 | \(DX=Var(X)=E(X-EX)^2\) |
| 协方差 | \(Cov(X,Y)=E\{\overline{[X-E(X)]}[Y-E(Y)]\}\) |
| 相关系数 | \(\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\) |
| 协方差矩阵 | \(\left[\begin{array}{ccc} Cov(X_1,X_1)&Cov(X_1,X_2)&\cdots&Cov(X_1,X_n)\\Cov(X_2,X_1)&Cov(X_2,X_2)&\cdots&Cov(X_2,X_n)\\ \vdots&\vdots&&\vdots \\Cov(X_n,X_1)&Cov(X_n,X_2)&\cdots&Cov(X_n,X_n)\end{array}\right]\) |
| 相关函数 | \(R(X,Y)=E[\overline{X}Y]\) |
| 均方极限 | \({l.i.m}_{n \to +\infty}X\) |
https://mp.weixin.qq.com/s/46NrpIako2lJ2ZitAQs8Sw
划重点！通俗解释协方差与相关系数
http://pinkyjie.com/2010/08/31/covariance/
浅谈协方差矩阵
平稳过程
严平稳过程：有限维分布。
宽平稳过程：二阶矩。
不要被名字迷惑了，由于两者关注的东西不同，一般情况下，严平稳过程不一定是宽平稳过程，宽平稳过程也不一定是严平稳过程。
只有以下特例：
1.对于二阶矩过程，严平稳过程一定是宽平稳过程。
2.对于正态过程，严平稳过程和宽平稳过程是等价的。
大数定律与中心极限定理
大数定律
切比雪夫大数定律：用统计方法来估计期望的理论依据。
\[E(X)\approx \frac{1}{n}\sum_{k=1}^{n}x_k\]贝努利大数定律：事件A发生的频率\(\frac{n_A}{n}\)依概率收敛于事件A的概率p。当n很大时，事件发生的频率与概率有较大偏差的可能性很小：\(p\approx \frac{n_A}{n}\)
中心极限定理
中心极限定理：研究何种条件下独立随机变量之和的极限分布为正态分布的一系列命题的统称。它是数理统计学和误差分析的理论基础，指出了大量随机变量积累分布函数逐点收敛到正态分布的积累分布函数的条件。自然界与生产中，一些现象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作是服从正态分布的。
独立同分布的中心极限定理
设相互独立的随机变量\(X_1,X_2,\dots,X_n\)具有相同的概率分布，且有有限的数学期望和方差：\(E(X_k)=\mu,D(X_k)=\mu ^2\neq 0(k=1,2,\dots,n)\)，则随机变量：
\[Y_n=\frac{\sum\limits_{k=1}^nX_k-n\mu}{\sqrt n\sigma}\]的分布函数\(F_n(x)\)对于任意实数x，都有：
\[lim_{n\rightarrow \infty}F_n(x)=\int_{-\infty}^x\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt\]由以上定理可知：
当n很大时，\(Y_n\)近似地服从标准正态分布N(0,1)。 令\(\overline{X}=\frac{1}{n}\sum_{k=1}^nX_k\)，则当n很大时，\(\overline{X}\)近似服从正态分布\(N(\mu,\frac{\sigma ^2}{n})\)。
由此可见：在独立同分布的情况下，无论\(X_1,X_2,\dots,X_n\)的分布函数为何，它们的平均数\(\overline{X}\)当n充分大的时候总是近似地服从正态分布。
独立不同分布的中心极限定理
若随机变量\(X_1,X_2,\dots,X_n\)相互独立，有有限的数学期望和方差，且满足林德贝格(Lindeberg)条件（每个随机变量都均匀小），则当n充分大时，这些变量之和的概率分布近似于正态分布。
我们可以这样理解大数定律和中心极限定理：
1、大数定律和中心极限定理可以看做随机变量的零阶和一阶“泰勒展开”，其中大数定律是随机变量的“零阶估计”，中心极限定理是在大数定律成立下的“一阶导数”，在极限下高阶小量可忽略。
2、大数定律负责给出估计——期望，中心极限定理负责给出大数定律的估计的误差——标准差乘以标准正态分布。
3、其实我们还可以进行更高阶的展开，貌似三阶展开对应的统计量叫做skewness，wiki上常用分布的词条都会给出这一数值。不过，在实际应用中，中心极限定理已经足够，所以通常也就不需要了。
参考：
https://mp.weixin.qq.com/s/LlAul8AoAUGUCgFP-qPvrA
中心极限定理通俗介绍
https://mp.weixin.qq.com/s/lc1oTETReXevVjK3NarbGg
大数定律和中心极限定理的区别和联系
https://blog.csdn.net/dawnranger/article/details/52950873
大数定律与中心极限定理
https://www.zhihu.com/question/22913867
怎样理解和区分中心极限定理与大数定律？
https://mp.weixin.qq.com/s/Prfc7biv2VJBcgNIMbn7Ow
如果数据分布是非正态的怎么办？用切比雪夫不等式呀！
https://mp.weixin.qq.com/s/SEXU8_SXXZ6OZkwK77OjQQ
随机矩阵的中心极限定理
Bézier curve
Bézier curve在数学界发现的时间很早——它是1912年由Sergei Natanovich Bernstein提出的。然而，真正将之发扬广大的，却是法国工程师Pierre Étienne Bézier。
Sergei Natanovich Bernstein，1880～1968，苏联数学家。University of Paris博士（1904），先后执教于University of Paris、University of Goettingen、University of Kharkiv、Leningrad University、Steklov Institute of Mathematics等名校和研究所。解决了Hilbert的第19个问题。
Pierre Étienne Bézier，1910～1999，École nationale supérieure d’arts etmétiers本科（1930）。终身供职于法国雷诺汽车公司。开发了最早的CAD/CAM系统（1960），被称为CAD/CAM之父。退休后，获得Pierre-and-Marie-Curie University博士学位（1977）。注意，这可不是荣誉学位，人家可是有重量级的博士论文的。
Bézier curve的数学公式比较复杂，但是实际的绘制方法却很简单。
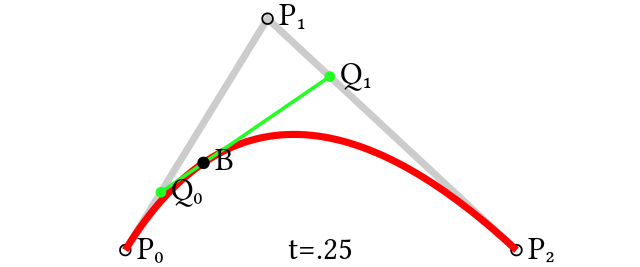
如上图所示。假设我们要绘制曲线\(C_{P_0P_2}\)上0.25位置上的点，那么可以在线段\(L_{P_0P_1}\)上找到0.25位置点\(Q_0\),在线段\(L_{P_1P_2}\)上找到0.25位置点\(Q_1\)，最后在线段\(L_{Q_0Q_1}\)上找到0.25位置点B，即为所求。
这个过程连续起来，就如下图所示：
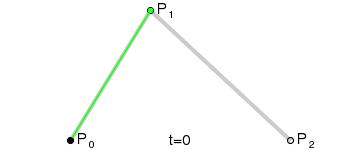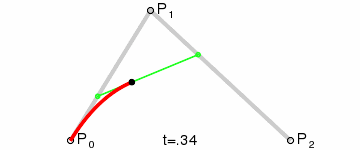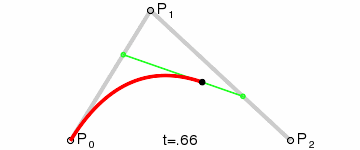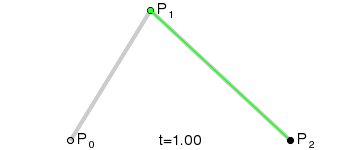
可见Bézier curve具有良好的数值稳定性，可产生类似皮筋的图像效应，是拟合光滑曲线的利器，因此被广泛应用于CAD/CAM领域。
Bézier curve也可用于超参数的search。
设\(f(X)=Y\)，其中X为超参数，Y为结果。则search的步骤如下：
1.为了得到特定的Y值，可以用Bézier curve插值得到相应的X值。
2.计算新的Y，将这个(X,Y)作为新的插值点，生成新的Bézier curve。
3.重复1，2步，直到收敛。
https://zhuanlan.zhihu.com/p/22679966
OpenGL实现贝塞尔曲线变幻屏保效果
熵
在《数学狂想曲（四）》的“玻尔兹曼分布”一节，我们提到了Shannon entropy的公式。然而，这个公式是如何推导出来的呢？
经典热力学定义
1803年，Lazare Carnot发现热机不能将所有的热量转换为机械能。1824年，其子Sadi Carnot在此基础上提出了理想热机的Carnot cycle。
Lazare Nicolas Marguerite, Count Carnot，1753～1823，法国政治家、数学家和物理学家。虽然他在热机方面作出了重大贡献，但他的名声主要还是在政治领域。他当过国民会议主席（法国大革命期间的国家元首），曾力排众议启用拿破仑作为远征意大利的主帅，算是拿破仑政治上的恩师。1793年法国共和政府推行征兵法之后，由Carnot一手组训出来的77万新军，开始投入战场并频获捷报，他因此被称为“胜利的组织者”，是极其优秀而成功的军备与后勤天才。在他的魔术棒下，无数平民出身的将才，如群星一样喷涌而出。
Nicolas Léonard Sadi Carnot，1796～1832，法国工程师和物理学家，被誉为“热力学之父”。Lazare Carnot之子。他的侄子Marie François Sadi Carnot后来成为了法国总统。
上图是一个理想热机的示意图，其中,\(T_H\)是高温热源温度，\(T_C\)是低温热源温度，\(Q_H\)是热机吸收的热量，而\(Q_C\)是热机释放的热量。W是热机产生的机械能。
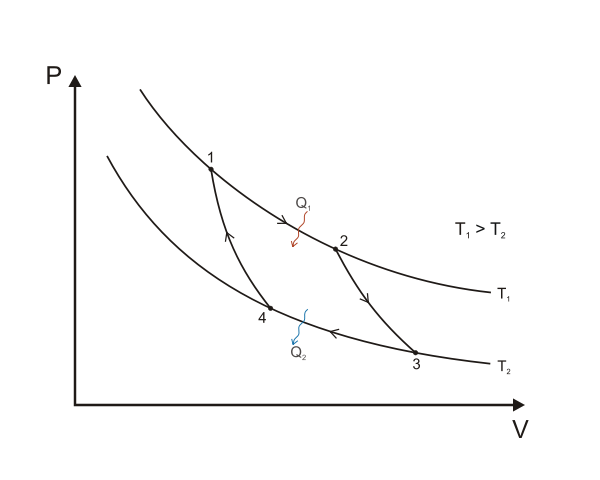
上图是Carnot cycle的PV图，其中，1->2（吸热）和3->4（放热）是等温过程，而2->3和4->1是绝热过程。
P-V图，是由James Watt发明的。
由热力学第一定律可得：
\[W=Q_H-Q_C\tag{1}\]理想气体方程：
\[pV=nRT\tag{2}\]等温过程：
\[p_1V_1=p_2V_2\tag{3}\]等温过程的作功公式为：
\[W=\int_{V_1}^{V_2}pdV=\int_{V_1}^{V_2}\frac{p_1V_1}{V}dV=p_1V_1\ln \frac{V_2}{V_1}=p_1V_1\ln \frac{p_1}{p_2}=nRT\ln \frac{p_1}{p_2}\tag{4}\]因为等温过程，内能不变，因此：
\[W=Q\]即：
\[Q_1=nRT_1\ln \frac{V_2}{V_1}\tag{5}\] \[Q_2=nRT_2\ln \frac{V_3}{V_4}\tag{6}\]绝热过程：
\[\left(\frac{V_2}{V_1}\right)^{\gamma-1}=\left(\frac{V_3}{V_4}\right)^{\gamma-1}\tag{7}\]由公式6、7可得：
\[Q_2=nRT_2\ln \frac{V_2}{V_1}\tag{8}\]由公式5、8可得：
\[\frac{Q_1}{T_1}=\frac{Q_2}{T_2}\tag{9}\]理想热机的效率：
\[\eta=\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1}=1-\frac{T_2}{T_1}\tag{10}\]公式10就是所谓Carnot’s theorem。Carnot发现所有热机的效率都不可能高于\(\eta\)。
您的打赏，是对我的鼓励
