• 函数连续性
  • Weierstrass Function（续）
  • 函数连续性和神经网络
  • KAN
  • 参考
• 莱洛三角形
• hinged dissections
• 核弹当量问题

函数连续性

Weierstrass Function（续）

上图是Weierstrass Function图像。它是一类处处连续而处处不可导的实值函数，其表达式为：

\[f(x)=\sum_{n=0} ^\infty a^n \cos(b^n \pi x)\]

其中，\(0<a<1\)，b是奇数，且\(ab > 1+\frac{3}{2} \pi\)。最小的满足该条件的值是\(b=7\)。

一般人会直觉上认为连续的函数必然是近乎可导的。即使不可导，所谓不可导的点也必然只占整体的一小部分。根据Weierstrass在他的论文中所描述，早期的许多数学家，包括高斯，都曾经假定连续函数不可导的部分是有限或可数的。这可能是因为直观上想象一个连续但在不可数个点上不可导的函数是很困难的事。

Weierstrass Function的出现（1872年）说明了所谓的“病态”函数的存在性，改变了当时数学家对连续函数的看法。

Weierstrass Function也被视为第一个分形函数（尽管分形（Fractal）的概念出现的相当晚（1973年），差不多过了整整一个世纪。）：将Weierstrass Function在任一点放大，所得到的局部图都和整体图形相似。因此，无论如何放大，函数图像都不会显得更加光滑，也不存在单调的区间。

参考：

https://wenku.baidu.com/view/21877fea551810a6f524868c.html

一个反例处处连续处处不可导的函数

https://mp.weixin.qq.com/s/ZwrWOZOlSibmM2vlfz1g6g

z = z^2 + c

函数连续性和神经网络

理论上说，多层神经网络只要有足够的深度和宽度，就可以任意逼近任意连续函数。（严格的说，这里的连续函数必须是Borel可测函数。）

然而从网络训练的角度来说，只有Lipschitz连续的函数才一定会收敛，否则的话，可能会出现梯度爆炸的情况。

此外，不同函数的收敛速度也不一样：

	GD	SGD
Lipschitz	\(\frac{1}{\sqrt{k}}\)	\(\frac{1}{\sqrt{k}}\)
+smoothness	\(\frac{1}{k}\)	\(\frac{1}{\sqrt{k}}\)
+strong convexity	\(\frac{1}{k}\)	\(\frac{1}{k}\)
+smoothness and strong convexity	\(\exp^{-k}\)	\(\exp^{-k}\)

KAN

Kolmogorov-Arnold representation theorem：

\[f(x) = f(x_1,...,x_n)=\sum_{q=1}^{2n+1}\Phi_q(\sum_{p=1}^n \phi_{q,p}(x_p))\]

KART是另一类函数逼近的方法。

Vladimir Igorevich Arnold，1937～2010，俄国数学家。莫斯科大学博士（1963），导师Kolmogorov。俄罗斯科学院院士，斯塔克罗夫数学研究所研究员。

https://www.zhihu.com/question/654782153

如何看待新网络架构KAN，它是否能取代MLP？

https://zhuanlan.zhihu.com/p/33570218

阿诺德：从“低能儿”到“奇异数学家”

参考

https://www.zhihu.com/question/32201415

函数连续和一致连续有什么区别？开区间上的连续函数不一定是一致连续的，为什么？

http://www.cnblogs.com/flywithyou/p/4135562.html

Lipschitz连续

https://www.zhihu.com/question/62554985

神经网络的上同调理论

http://tech.scichina.com:8082/sciE/CN/abstract/abstract404403.shtml

神经网络的本质逼近阶

http://www.doc88.com/p-2337088655000.html

神经网络的函数逼近理论

https://zhuanlan.zhihu.com/p/25590725

神经网络为什么能够无限逼近任意连续函数？

https://max.book118.com/html/2015/0401/14126427.shtm

浅谈Borel可测函数及其性质

https://mp.weixin.qq.com/s/jrNIhSlTiXsO2sGWmzcFfg

Michael I. Jordan最新清华授课笔记！

https://mp.weixin.qq.com/s/hDRLyOFpLUSW6ZDamwPiAg

相较神经网络，大名鼎鼎的傅里叶变换，为何没有一统函数逼近器？

莱洛三角形

定宽曲线（Curve of constant width），或称恒宽曲线，定义：平面上一凸形封闭曲线，不论如何转动，其宽度永远不变，则称之定宽曲线或恒宽曲线。这里所称的“宽度”是指平行线“夹住”某封闭曲线时，平行线间的距离，所谓”夹住”是指每个平行线与凸形封闭曲线相交至少一点且与凸形封闭曲线围起来的内部区域（interior）不相交。

或者可以说，将一个闭合曲线放在两条平行线中间，使之与这两平行线相切，则可以做到：无论这个闭合曲线如何运动，只要它仍与原平行线中的一条直线相切，就必与另一条直线线相切，那么此闭合曲线为定宽曲线。

上图是定宽曲线的一个直观的解释。平板下方的两个轮子转动的过程中，平板和桌面的距离保持不变。

这两个轮子一个是圆形，另一个就是本篇的主角——莱洛三角形（Reuleaux triangle）。

Franz Reuleaux，1829～1905，德国人。这个人可谓是全才。
在教育界，当过ETH和柏林工业大学的教授和校长，当然了那个时代这两所学校还不叫现在的名字。
在工业界，他发明了300多种机械模型，被誉为动力学（kinematics）之父。 在政界，他是1876年世界工业博览会德国代表团的主席，参与创立了德国的专利体系。

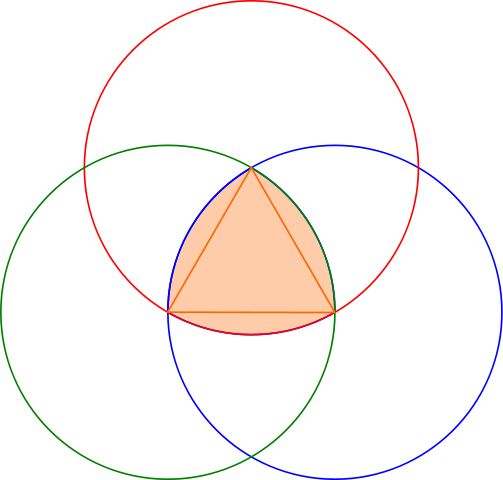
上图是Reuleaux triangle的尺规做图方法。

Reuleaux triangle是“除了圆形以外，还有什么形状的下水道盖不会掉入下水道？”这个问题的一个答案。这也是所有定宽曲线的特性。但Reuleaux triangle的特殊之处在于：它是定宽曲线所能构成的面积最小的图形。因此它做的井盖非常省铁。

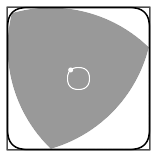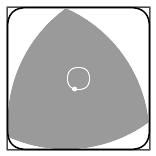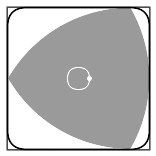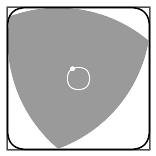
上图展示了零件上的方孔是如何钻出来的。类似的还有：

后者叫做delta curves，不过它并不是个定宽曲线。

动力学是一门研究机械以及组成机械的各个部件之间的运动关系的科学，被广泛应用于机械设计领域。比如：

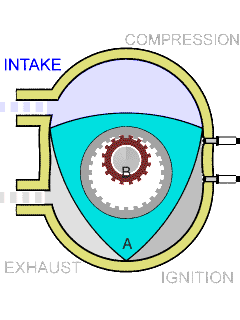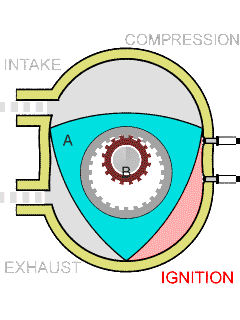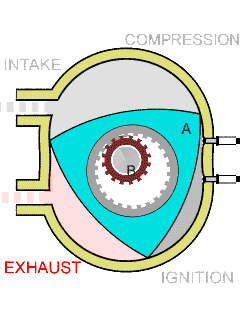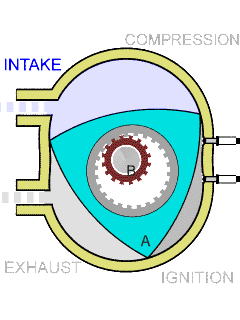
上图是一个没有活塞的发动机气缸，转子的形状就是类Reuleaux triangle的。

这里由于汽缸不是方形的，因此只是一个类Reuleaux triangle。

当然，Reuleaux triangle也有它的问题：

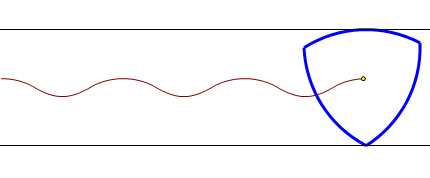
Reuleaux triangle形状的轮子，在上面铺板子跑，当然毫无问题。但如果安装车轴的话，那就蛋碎了…

所以，又有了下面这样的逆问题：

如何让方轮车平稳地行驶呢？只要让波浪轨道符合一段一段的悬链线方程。

参考：

https://en.wikipedia.org/wiki/Curve_of_constant_width

https://en.wikipedia.org/wiki/Reuleaux_triangle

https://en.wikipedia.org/wiki/Reuleaux_tetrahedron

http://www.cnblogs.com/hxsyl/archive/2012/07/05/2578448.html

莱洛三角形和定宽曲线

http://twistedsifter.com/2012/11/animated-gifs-that-explain-how-things-work/

20 Animated Gifs that Explain How Things Work

https://mp.weixin.qq.com/s/uUUhQ6tJMrn3J5Ko2u1Hiw

三角形中惊现叛徒！自己胖的像个球，却能成就世界上最快的赛车引擎……

https://mp.weixin.qq.com/s/463KqrYA968HjaBBlsdmow

小伙打造一辆奇葩自行车，走路上百分百的回头率

hinged dissections

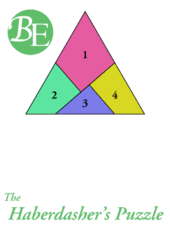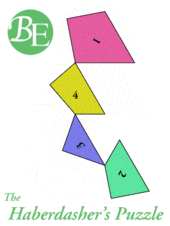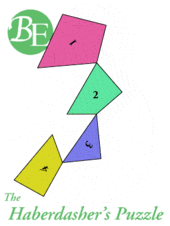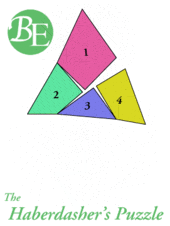
Henry Ernest Dudeney，1857～1930，英国上世纪最知名的数学科普作家。

核弹当量问题

核弹爆炸由于是个复杂的过程，因此就有了爆炸火球半径、辐射半径、冲击波半径以及热辐射半径等不同的威力评价标准。

具体的介绍可参见：

https://www.zhihu.com/question/20134458

一颗核弹的破坏性有多大？

这里给出几组数据：

名称	当量	火球半径	冲击波半径
1945年胖子	20kt	200m	1.91km
1966年B61	340kt	630m	4.91km
1986年W87	300kt	600m	4.71km

“另外再帮你算算哦，把B61的34万和胖子的2万都开根号，两者比值是4.11，然而，胖子的火球半径200米乘4.1貌似是820米，怎么B61才630米呢？5psi的冲击波半径1.91千米乘4.1貌似是7.83千米哦，怎么B61才4.91呢？不是说好了技术进步威力更大的吗”

上面是贴吧某博主用以佐证自己观点的论据。然而，这显然错误的。

冲击波是空气被压缩导致的。而空气可以看做麦克思韦子，它的压力是由单位体积内的粒子能量决定的。因此，如果当量E可以产生R半径的空气压缩球的话，要产生2R的压缩球，势必需要将E提升8倍才行。

而火球半径就要麻烦一些了。

一方面，辐射的光子是玻色子，它不占空间，能量可叠加，且不改变传播方向。从点光源的波动模型可以知道，波前能量如果没有衰减的话，R球面的能量和2R球面的能量相等，但2R球面的面积是前者的4倍，因此如果要维持能量密度的话，E提升4倍即可。

另一方面，辐射源需要维持一定的温度才能释放可见光，而温度也就是粒子平均动能，正如上面冲击波半径的推导，E和R的立方成正比。

所以，火球半径中E和R的关系，显然在2和3之间。实际上，它的理论值就是2.5，其推导过程如下：

http://www.applet-magic.com/fireball.htm

The Expansion of the Fireball of an Explosion

推导主要用到了物理学的等式两边量纲齐次的原则，并不是很复杂。

实测值2.46和理论值符合的非常好。

这里的推导和热力学统计其实没多大关系，算是本人学习玻尔兹曼分布的副产品吧。

以下来几个实际爆炸的例子：

https://mp.weixin.qq.com/s/VOeBV4gufdeV1FQ1ol2whA

爆炸的能量（当量）有多大？

---

1947年4月16日，美国得克萨斯州得克萨斯城一艘停泊在加尔维斯敦湾内的法国货轮起火，致使船上运载的约2300吨硝酸铵爆炸，进而引发附近船只与储油设施爆炸。这也是人类历史上最大的一次意外非核（工业）爆炸！

https://www.zhihu.com/question/412103180

黎巴嫩首都发生巨大爆炸，或由存放的2700吨硝酸铵引起，目前情况如何？

https://mp.weixin.qq.com/s/V5gymAXJBMmN0Nqbwte2hQ

黎巴嫩港口大爆炸到底有多厉害？