数学狂想曲（七）——双曲函数和悬链线, 函数连续性
2017-09-22概率分布（2）
KS检验（续）
上图的红线是某随机变量假设分布的CDF，而蓝线是该随机变量样本的累积分布曲线，即ECDF（Empirical Distribution Function）。
显然若假设正确的话，两条曲线应该是基本重合的。反之，若两条曲线差异较大，则该假设检验不成立。这就是KS检验的基本原理。
KS检验的统计量定义如下：
\[D_n= \sup_x |F_n(x)-F(x)|\]其中\(\sup\)表示最小上界，
\[F_n(x)={1 \over n}\sum_{i=1}^n I_{[-\infty,x]}(X_i)\] \[I_{[-\infty,x]}(X_i)=\begin{cases} 1, & X_i \le x \\ 0, & \text{otherwise} \\ \end{cases}\]KS检验更深入的解释，涉及到布朗运动和维纳过程，这里不再赘述。
参考：
https://mp.weixin.qq.com/s/YMKHw3qgWvhEz4f8nPw7Cg
5种数据同分布的检测方法
Pearson distributions
Pearson distributions是1895年左右由英国统计学家卡尔·皮尔逊提出的一组频率分布。它打破了“正态分布是全能的”传统观念，在数理统计发展史上是一个重大突破。
偏态分布：“正态分布”相对，分布曲线左右不对称的数据次数分布，是连续随机变量概率分布的一种。可以通过峰度和偏度的计算，衡量偏态的程度。可分为正偏态和负偏态，前者曲线右侧偏长，左侧偏短；后者曲线左侧偏长，右侧偏短。
概率密度\(f(x)\)决定于微分方程：
\[\frac{\mathrm{d}f(x)}{\mathrm{d}x}=\frac{(a_0+a_1x)f(x)}{b_0+b_1x+b_2x^2}\]https://variation.com/wp-content/distribution_analyzer_help/hs130.htm
Pearson Family of Distributions
百年一遇
Gumbel distribution是一种根据频率曲线来计算“多年一遇”海洋水文气象要素的常用方法。Gumbel分布以Emil Julius Gumbel（1891-1966）命名。
https://www.zhihu.com/question/21315165
为什么所谓五十年一遇、百年一遇的自然灾害几乎年年发生？
双曲函数和悬链线
悬链线 (Catenary) 是一种曲线，因其与两端固定的绳子在均匀引力作用下下垂相似而得名。适当选择坐标系后，悬链线的方程是一个双曲余弦函数。
悬链线背后的故事和推导，百度百科已经比较详细了，不再赘述。参见：
http://baike.baidu.com/view/45656.htm
然而对于实际工程中的悬索结构，由于悬索自身的重量较其所提拉的跨度结构要轻得多，在力学简单计算中可以忽略，结构受力模式成为在水平长度范围内的均布荷载。这种荷载模式与拱结构相同，因此可以推导出在该荷载模式下的悬垂线为一抛物线，线型与拱结构相同，但内力为拉力。
在工程中完全按照悬链线进行设计的结构，恐怕只有高压输电线了。由于不承担任何自重以外的附加荷载，输电线的数学曲线会与悬链线完全一致。
双曲函数的性质，参见：
https://zhuanlan.zhihu.com/p/20042215
可能是最好的讲解双曲函数的文章
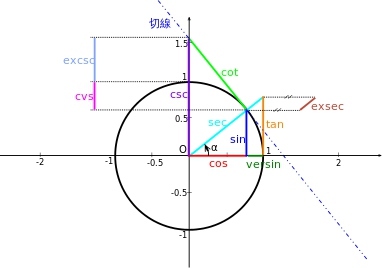
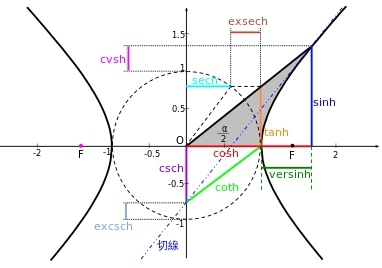
参考：
https://mp.weixin.qq.com/s/VOPis0wgmi-U-uM3Vnapbw
这根链子什么来头？
数学杂谈
当年洛伦茨求解这3个变量的方程组用的是一台Royal McBee LGP-30计算机，放置在MIT第24号楼第五层。这台机器比书桌还大，重约260公斤，可是速度极其缓慢，连今天的笔记本电脑都比它快上一百万倍。
当年，计算机程序是由两位年轻女助手艾伦·费特（Ellen Fetter）和玛格丽特·哈密顿（Margaret Hamilton）负责编写的。她们都是来到洛伦茨实验室工作后才开始学习编写计算机程序。
这位Margaret Hamilton就是后来编写阿波罗登月程序的女主。
https://mp.weixin.qq.com/s/REiUxKrLCRWeRCusVlooYQ
蝴蝶效应和混沌故事（Edward Norton Lorenz）
如果你往高尔顿板里倒入很多小球，一个惊人的规律就出现了：在底部堆积的小球的上边缘总是会形成一个近似钟形的曲线。在最接近中心的插槽中，小球会堆得高高的，插槽中的球数从中间向两侧递减，直至为零。
https://mp.weixin.qq.com/s/BwMAiziWQuyKaru8xB9tHw
一文读懂因果推断的起源
函数连续性
函数连续性本质上是刻画函数在自变量变化的情况下，函数值变化的稳定程度。
连续函数（Continuous function）
\[\forall x \in I \; \forall \epsilon > 0 \; \exists \delta > 0 \; \forall y \in I ; \, |x - y|<\delta \, \Rightarrow \, |f(x) - f(y)| < \epsilon\]连续函数有很多种等价定义，为了方便和之后的一致连续进行对比，这里选用量词（Quantifier）逻辑的定义。
这个定义实际上是个Nest定义。以\(\exists\)为界，整个Quantifier被分成3部分：定值、存在变量、变量。上边的例子实际上是说：在给定\(x, \epsilon\)的情况下，存在\(\delta\)，对所有y，结论都成立。
因为x不变，所以这实际上是个定点连续的条件。因此，这种连续又叫做Pointwise continuity。
通俗的说法：f的函数曲线在区间内没有断点。
一致连续（Uniform continuity）
\[\forall \epsilon > 0 \; \exists \delta > 0 \; \forall x, y \in I ; \, |x - y|<\delta \, \Rightarrow \, |f(x)-f(y)|<\epsilon\]Uniform continuity比Pointwise continuity要严格一些，因为x,y都是变量。
Uniform continuity的形象解释如下所示：
上图中蓝框和红框的顶部和底部用粗线表示，在方框的运动过程中，红线始终没有穿过方框的顶部或底部，所以它是Uniform continuity的，而蓝线不是。
\(f(x)=\frac{1}{x}\)不是Uniform continuity的最大原因在于\(x\to 0,f(x)\to \infty\)，由于值域没有上界，因此，对于给定的\(\delta\)，\(\epsilon\)也是没有上界的。
但如果定义域限定为闭区间，则值域必有界。这时，Uniform continuity和Pointwise continuity是等价的。
绝对连续（Absolute continuity）
\[\forall \varepsilon > 0 \; \exists \delta > 0 \; \forall (x_k, y_k) \in I ; \, \sum_k (y_k - x_k) < \delta \, \Rightarrow \, \sum_k | f(y_k) - f(x_k) | < \varepsilon\]Absolute continuity不仅要求整个函数满足Uniform continuity，而且任意子区间也要满足该条件。因此，Absolute continuity比Uniform continuity更严格。
Lipschitz连续
\[\forall x_1,x_2 \in I ;\mid f(x_1) - f(x_2)\mid \le K \mid x_1 - x_2\mid , K>0\text{ is const}\]注：Rudolf Otto Sigismund Lipschitz，1832～1903，德国数学家，先后就读于柯尼斯堡大学和柏林大学，导师Dirichlet。波恩大学教授。
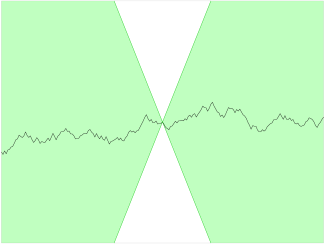
Lipschitz连续的直观图示如上所示。该曲线上的所有点的切线斜率的绝对值\(\le K\)。
易知，Lipschitz continuity比Absolute continuity更严格。
上式中的K被称为该函数的Lipschitz常数，因此,也可说\(f(x)\)是K-Lipschitz连续的。
连续可微
这个的定义比较简单：函数的导数是连续的。直观来说就是：函数曲线光滑，没有尖。
由“闭区间的连续函数必有界”可知，闭区间的Continuously differentiable一定是Lipschitz continuity的。
综上：
\[\text{Continuously differentiable} \subseteq \text{Lipschitz continuous} \subseteq \text{Absolute continuity} \subseteq \text{uniformly continuous} = \text{continuous}\]需要注意，这些结论只在闭区间成立。比如\(f(x)=x^2\)是连续可微的，但却不是一致连续的。因此又有Local Uniform continuity之类的说法。
\((1/\gamma)\)-smooth
如果\(f(x)\)是可微的，且\(\nabla f(x)\)是\((1/\gamma)\)-Lipschitz的，则如果
\[f(b)\le f(a)+\nabla f(a)^{\top}(b-a)+\frac{1}{2\gamma}\|b-a\|_2^2\]那么，\(f(x)\)是\((1/\gamma)\)-smooth的。
\(\lambda\)-strongly convex
\[f(b)\ge f(a)+\nabla f(a)^{\top}(b-a)+\frac{\lambda}{2}\|b-a\|_2^2\]Weierstrass Function
Karl Theodor Wilhelm Weierstrass，1815～1897，德国数学家，被誉为“现代分析之父”。
青年时代，Weierstrass被父亲送到波恩大学学习法律和商业，然而他对此根本不感兴趣，精力都花到数学上了，这直接导致他离开大学时，没有拿到学位。
此后经过努力，他获得了一份中学数学教师的职位。他30～40岁的时光，就是在两所不知名的中学度过的。
所幸，他的努力没有白费。1854年，他获得格尼斯堡大学荣誉博士学位。此后先后任教于柏林工业大学和柏林洪堡大学。
他的博士学生知名的有：集合论创始人Georg Cantor，世界历史上第一位数学女博士Sofia Kovalevskaya和Hermann Schwarz（没错就是提出Cauchy–Schwarz inequality的那位）。
事实上，本文中使用的\(\varepsilon - \delta\)定义，就是Weierstrass的成果。Weierstrass首次采用数学的方式定义极限，取代了之前Newton的物理或几何式的极限定义。
物理或几何式的极限定义有着直观的优势，但不够严格，Weierstrass Function就是最好的反例。
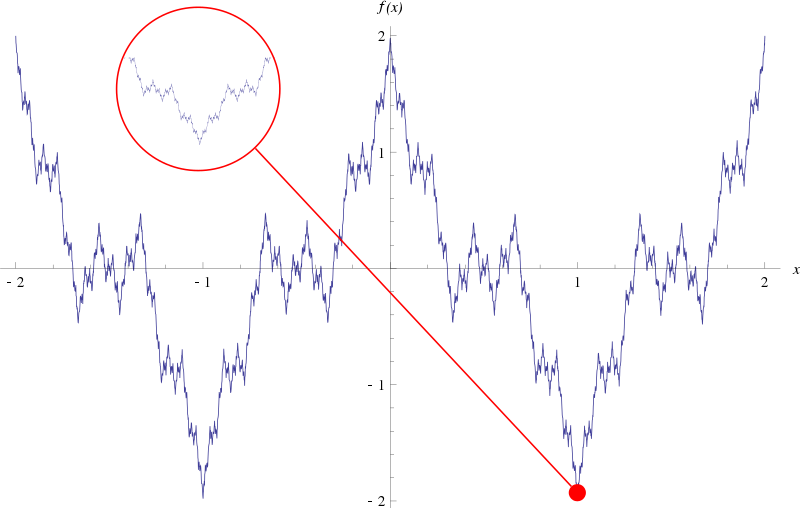
上图是Weierstrass Function图像。它是一类处处连续而处处不可导的实值函数，其表达式为：
\[f(x)=\sum_{n=0} ^\infty a^n \cos(b^n \pi x)\]其中，\(0<a<1\)，b是奇数，且\(ab > 1+\frac{3}{2} \pi\)。最小的满足该条件的值是\(b=7\)。
一般人会直觉上认为连续的函数必然是近乎可导的。即使不可导，所谓不可导的点也必然只占整体的一小部分。根据Weierstrass在他的论文中所描述，早期的许多数学家，包括高斯，都曾经假定连续函数不可导的部分是有限或可数的。这可能是因为直观上想象一个连续但在不可数个点上不可导的函数是很困难的事。
Weierstrass Function的出现（1872年）说明了所谓的“病态”函数的存在性，改变了当时数学家对连续函数的看法。
Weierstrass Function也被视为第一个分形函数（尽管分形（Fractal）的概念出现的相当晚（1973年），差不多过了整整一个世纪。）：将Weierstrass Function在任一点放大，所得到的局部图都和整体图形相似。因此，无论如何放大，函数图像都不会显得更加光滑，也不存在单调的区间。
参考：
https://wenku.baidu.com/view/21877fea551810a6f524868c.html
一个反例处处连续处处不可导的函数
https://mp.weixin.qq.com/s/ZwrWOZOlSibmM2vlfz1g6g
z = z^2 + c
