math » 数学狂想曲(六)——概率分布(2)
2017-03-05 :: 6837 Words玻尔兹曼分布(续)
参考
http://wenku.baidu.com/view/ccb7956db84ae45c3b358ca7.html
波尔兹曼统计分布律的推导的新方法
http://www.cnblogs.com/tianchi/archive/2013/03/14/2959716.html
Boltzmann machine
https://mp.weixin.qq.com/s/Z1_ujG7iP_AFUD0gVO8HXQ
信息熵、交叉熵和相对熵
https://mp.weixin.qq.com/s/2_ZkKrwPhaS31JnyYXyfrQ
简单的交叉熵损失函数,你真的懂了吗?
http://blog.csdn.net/shijing_0214/article/details/51116046
理解最大熵模型
https://mp.weixin.qq.com/s/yUJDMSU1Fmf36vN2Q2y1TA
最大熵模型原理小结
https://mp.weixin.qq.com/s/a3TlUFwSm9aIptfhy6MnGA
机器学习是如何借鉴物理学思想的?从伊辛模型谈起
https://mp.weixin.qq.com/s/_DxdlaJahSscXe4O2fw1uA
伊辛模型百年小史:最经典的复杂系统模型,却险些被科学界遗忘
https://zhuanlan.zhihu.com/p/39241895
深度学习与物理,有效场论,重整化群
https://mp.weixin.qq.com/s/7NrB0UtmELXD3UNO3C6jGA
我就不信看完这篇你还搞不懂信息熵
https://mp.weixin.qq.com/s/_s8kxlzcL5Nt2ILUIfAuNQ
不要把所有的鸡蛋放在一个篮子里–谈谈最大熵模型
概率分布(2)
上一篇《概率分布(1)》写的意犹未尽,这里继续写。本篇主要关注\(\chi^2\)分布、t分布和F分布,也就是统计学的三大祖师爷各自的看家本领。
\(\chi^2\)分布
设\(X_1,\dots,X_n\)是来自总体\(N(0,1)\)的样本,则称统计量
\[\chi^2=X_1^2+\dots+X_n^2\tag{1}\]服从自由度为n的\(\chi^2\)分布(chi-squared distribution),记作\(\chi^2\sim \chi^2(n)\)。其PDF为:
\[f(x;\,n) = \begin{cases} \dfrac{x^{(n/2-1)} e^{-x/2}}{2^{n/2} \Gamma\left(\frac n 2 \right)}, & x > 0; \\ 0, & \text{otherwise}. \end{cases}\]t分布
设\(X\sim N(0,1),Y\sim\chi^2(n)\),并且X、Y独立,则称随机变量
\[t=\frac{X}{\sqrt{Y/n}}\tag{2}\]服从自由度为n的t分布(t distribution),记作\(t\sim t(n)\)。其PDF为:
\[f(t) = \frac{\Gamma(\frac{n+1}{2})} {\sqrt{n\pi}\,\Gamma(\frac{n}{2})} \left(1+\frac{t^2}{n} \right)^{\!-\frac{n+1}{2}}\]F分布
设\(U\sim \chi^2(d_1),V\sim\chi^2(d_2)\),并且U、V独立,则称随机变量
\[F=\frac{U/d_1}{V/d_2}\tag{3}\]服从自由度为\((d_1,d_2)\)的F分布(F distribution),记作\(F\sim F(d_1,d_2)\)。其PDF为:
\[\begin{align} f(x; d_1,d_2) &= \frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}} {(d_1\,x+d_2)^{d_1+d_2}}}} {x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)} \\ &=\frac{1}{\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)} \left(\frac{d_1}{d_2}\right)^{\frac{d_1}{2}} x^{\frac{d_1}{2} - 1} \left(1+\frac{d_1}{d_2}\,x\right)^{-\frac{d_1+d_2}{2}} \end{align}\]显然:
\[\frac{1}{F}\sim F(d_2,d_1)\]参考:
https://mp.weixin.qq.com/s/X0nSqiQoJpEur7PM1tM-0A
每个数据科学专家都应该知道的六个概率分布
https://www.zhihu.com/question/26991510
卡方独立性检验和卡方齐性检验的区别是什么?
https://mp.weixin.qq.com/s/vcgZ2ncZDlXp4SAExyptnQ
Distribution is all you need:这里有12种做ML不可不知的分布
假设检验
假设检验就是根据样本对所提出的假设\(H_0\)作判断。
如果\(P\{拒绝H_0\mid H_0为真\}\le \alpha\),则接受\(H_0\)。
这里的\(\alpha\)被称作显著性水平。假设检验\(H_0\)所涉及的统计量被称作检验统计量。
在英国的Rothamsted实验站,Fisher给一位名叫Muriel Bristol的女士倒了一杯茶,但是Bristol表示,自己更喜欢先将牛奶倒入杯中,再倒入茶。这位女士号称能够分辨先倒茶和先倒牛奶的区别。
作为实验设计的鼻祖,Fisher当然想用实验检验一下:这位女士的味觉是否有这么敏锐?Fisher倒了8杯奶茶:其中4杯“先奶后茶”,其余4杯“先茶后奶”。随机打乱次序后,Fisher请Bristol品尝,并选出“先奶后茶”的4杯,看她是否能分辨奶和茶的顺序。
Bristol完全答对了。这是一个小概率事件,概率小于0.05(通常的统计显著性水平)。所以,她“没有任何分辨能力”这个假设就和数据不太相容,可以拒绝这个假设。
下表是正态总体均值、方差的检验法表格:
| \(H_0\) | 检验统计量 | \(H_0\)为真时的统计量分布 |
|---|---|---|
| \(\mu=\mu_0(\sigma^2已知)\) | \(z=\frac{\overline x-\mu_0}{\sigma/\sqrt n}\) | \(N(0,1)\) |
| \(\mu=\mu_0(\sigma^2未知)\) | \(t=\frac{\overline x-\mu_0}{s/\sqrt n}\) | \(t(n-1)\) |
| \(\mu_1-\mu_2=\delta(\sigma_1^2,\sigma_2^2已知)\) | \(Z=\frac{\overline x-\overline y-\delta}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\) | \(N(0,1)\) |
| \(\mu_1-\mu_2=\delta(\sigma_1^2=\sigma_2^2=\sigma^2未知)\) | \(t=\frac{\overline x-\overline y-\delta}{s_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}},s_w^2=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}\) | \(t(n_1+n_2-2)\) |
| \(\sigma^2=\sigma_0^2(\mu未知)\) | \(\chi^2=\frac{(n-1)s^2}{\sigma_0^2}\) | \(\chi^2(n-1)\) |
| \(\sigma_1^2=\sigma_2^2(\mu_1,\mu_2未知)\) | \(F=\frac{s_1^2}{s_2^2}\) | \(F(n_1-1,n_2-1)\) |
| \(\mu_d=0(成对数据)\) | \(t=\frac{\overline d-0}{s/\sqrt n}\) | \(t(n-1)\) |
上面这些和\(\chi^2\)分布、t分布、F分布有关的假设检验,又被称作\(\chi^2\)检验、t检验和F检验。对均值的假设检验,被称为\(\mu\)检验。
一元线性回归的显著性检验
假设y关于x的回归具有形式\(a+bx\),则\(H_0:b=0\)。
这里使用t检验法进行假设检验。
首先,不加证明的给出如下结论:
推论1:\(\overline y\sim N(a+b\overline x,\sigma^2/n)\)
推论2:\(\hat b\sim N(b,\sigma^2/S_{xx})\)
推论3:\(\hat y_0=\hat a+\hat b x_0=\overline y+\hat b(x_0-\overline x)\sim N\left(a+bx_0,\left[\frac{1}{n}+\frac{(x_0-\overline x)^2}{S_{xx}}\right]\sigma^2\right)\)
推论4:\(Q_e/\sigma^2\sim \chi^2(n-2)\)
推论5:\(\overline y,\hat b,Q_e\)相互独立。
推论6:若\(y_0=a+bx_0+\epsilon_0\)与\(y_1,\dots,y_n\)独立,则\(y_0,\hat y_0,Q_e\)相互独立。
其中,\(\overline y\)表示y的均值,而\(\hat y\)表示y的估计值,\(S_{xx}\)表示方差,\(Q_e\)为残差平方和\(\sum_{i=1}^n(y_i-\hat y_i)^2\)。
由推论4可得:
\[E(Q_e/\sigma^2)=n-2\]即:
\[Q_e=\hat\sigma^2(n-2)\tag{4}\]由推论2和5、公式2和4,可得:
\[\frac{\hat b-b}{\sqrt{\sigma^2/S_{xx}}}\bigg /\sqrt{\frac{(n-2)\hat \sigma^2}{\sigma^2}\bigg /(n-2)}\sim t(n-2)\]即:
\[\frac{\hat b-b}{\hat \sigma}\sqrt{S_{xx}}\sim t(n-2)\]当假设\(H_0\)被拒绝时,认为回归效果是显著的,反之就认为回归效果不显著。
不显著的原因可能有以下几种:
1.影响y取值的,除了x,还有其他不可忽略因素。
2.y与x的关系不是线性的,存在其他的关系。
3.y与x不存在关系。
上面这些都是正态样本的参数检验。
对于非参数检验或者非正态样本检验,其他的检验方法还有Wilcoxon signed-rank test、Kruskal–Wallis test、Friedman test等。
Frank Wilcoxon,1892~1965,美国化学家。康奈尔大学博士。先后供职于几家美国化工企业的研究机构。
William Henry (“Bill”) Kruskal,1919~2005,美国数学家。哥伦比亚大学博士,芝加哥大学教授。
Milton Friedman,1912~2006,美国经济学家。哥伦比亚大学博士,芝加哥大学教授。1976年获诺贝尔经济学奖。芝加哥学派第二代的领军人物。
Wilson Allen Wallis,1912~1998,美国经济学家。先后就读于明尼苏达大学和芝加哥大学,但是没有博士学位。罗彻斯特大学校长。从艾森豪威尔到里根的历届共和党总统的顾问。Milton Friedman的至交。其父Wilson Dallam Wallis为美国人类学家,明尼苏达大学教授。
参考:
https://mp.weixin.qq.com/s/xd2Xw093Wp7O7yQLZHSL4Q
一文学会统计学中的显著性概念
https://mp.weixin.qq.com/s/9-sWv5QDcNYSSYOfuEIcQg
“假设”家族大起底!如何正确区分科学假设、统计假设和机器学习假设?
https://mp.weixin.qq.com/s/pCDSyFOd7D_pKYYvxEkqwQ
女士品茶的实验、假设和检验
https://mp.weixin.qq.com/s/u30ikol5V9t4eRUNhYtoQg
p值是什么?数据科学家用最简单的方式告诉你
https://mp.weixin.qq.com/s?__biz=MjM5NDQ3NTkwMA==&mid=2650144001&idx=1&sn=10b9fc6e066ce85dcb7a8836947aea87
常见统计检验的本质是线性模型
https://mp.weixin.qq.com/s/LEfTGM2uliZA99ngTomCdw
使用假设检验分析PS4,XBox,Switch谁是最好的游戏主机
https://mp.weixin.qq.com/s/FZeTUkPBOonAk3VEZK-zWQ
常见分布与假设检验
KS检验
Kolmogorov–Smirnov test用于对样本是否属于某种分布进行假设检验。
Andrey Nikolaevich Kolmogorov,1903~1987,二十世纪俄国最伟大的数学家之一。莫斯科州立大学博士和教授。俄罗斯科学院院士,挪威科学院和英国皇家学会外籍院士。沃尔夫奖获得者(1980年)。他在数学的许多领域都有重要贡献,以他的名字命名的理论竟有30项之多。
https://mp.weixin.qq.com/s/uJKXvp-qtMH-PNNLieUdTg
现代概率论之父:柯尔莫哥洛夫的“随机”人生
Nikolai Vasilyevich Smirnov,1900~1966,俄国数学家。莫斯科大学博士,斯塔克罗夫数学研究所研究员。
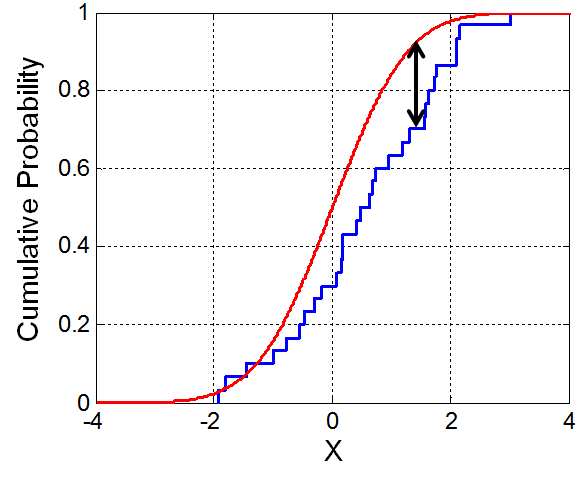
上图的红线是某随机变量假设分布的CDF,而蓝线是该随机变量样本的累积分布曲线,即ECDF(Empirical Distribution Function)。
显然若假设正确的话,两条曲线应该是基本重合的。反之,若两条曲线差异较大,则该假设检验不成立。这就是KS检验的基本原理。
KS检验的统计量定义如下:
\[D_n= \sup_x |F_n(x)-F(x)|\]其中\(\sup\)表示最小上界,
\[F_n(x)={1 \over n}\sum_{i=1}^n I_{[-\infty,x]}(X_i)\] \[I_{[-\infty,x]}(X_i)=\begin{cases} 1, & X_i \le x \\ 0, & \text{otherwise} \\ \end{cases}\]KS检验更深入的解释,涉及到布朗运动和维纳过程,这里不再赘述。
参考:
https://mp.weixin.qq.com/s/YMKHw3qgWvhEz4f8nPw7Cg
5种数据同分布的检测方法
Vladimir Andreevich Steklov,1864~1926,俄国数学家、物理学家。哈尔科夫大学博士,其导师是圣彼得堡学派第二代人物中,仅次于Andrey Markov的Aleksandr Lyapunov。哈尔科夫大学和圣彼得堡大学教授,1919年创建斯塔克罗夫数学研究所。
斯塔克罗夫数学研究所是一家专职研究没有教学任务和科研任务的研究机构。Grigori Perelman在这里,曾有6年时间没有发表一篇论文。二十世纪俄罗斯绝大多数的数学发现都源自这里。

您的打赏,是对我的鼓励
