• 抛物线
• 肺炎版《黄冈密卷》
• 玻尔兹曼分布
  • 信息熵
  • 最大信息熵原理
  • 相关名词辨析
  • 玻尔兹曼分布的推导

抛物线

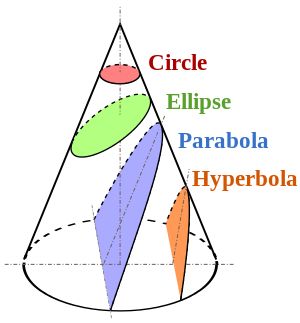
我们都知道抛物线只有一个焦点，而椭圆、双曲线有两个焦点，但是对于真正天体的运行来说，其实只有一个焦点是有意义的，就是中心恒星的位置；另一个焦点没有实在的意义。这两个焦点中任取一个就可以构成这条圆锥曲线，而取哪一个作为恒星位置都是一样的。因为对于椭圆、双曲线来说，这两个焦点是对称的。

那么抛物线呢？实际上抛物线是椭圆和双曲线的临界状态，它的另一个焦点在无穷远的地方。对于绕恒星的抛物线轨道来说，取的是那个通常说的焦点位置作为恒星位置；对于地面上的斜抛运动来说，取的是无穷远处的那个焦点位置作为恒星位置。

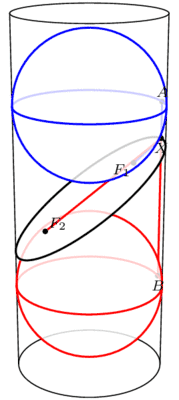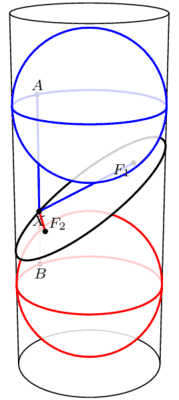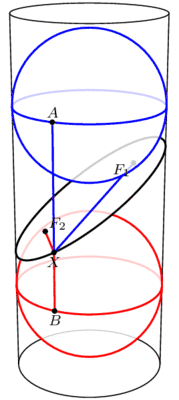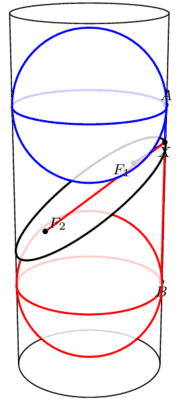
我们从斜面的上方和下方分别塞进一个球，它们与圆柱、截面均相切，然后，两个球与截面相切的点就是椭圆的两个焦点。

https://mp.weixin.qq.com/s/BmSdlLTZ8PxD_b27TzFWlw

如何让8岁表妹了解数学到底是什么

https://mp.weixin.qq.com/s/p-EVuaPfLusq01Jw8KcQdQ

六一礼物：这些有趣的动图送给孩子们！了解数学能做什么？电路如何工作？

肺炎版《黄冈密卷》

问题由来：

https://mp.weixin.qq.com/s/dR7fg6PTCVAnezlW6gTY2w

新冠病毒最“强”管控，《黄冈密卷》数学题到底有多难

---

1.设\(\sqrt{3+\sqrt{2}+\sqrt{3}+\sqrt{6}}=\sqrt{x}+\sqrt{y}+\sqrt{z}\)，且x、y、z为有理数，则\(xyz\)=?

解：

\[3+\sqrt{2}+\sqrt{3}+\sqrt{6} = x+y+z+2\sqrt{xy}+2\sqrt{xz}+2\sqrt{yz}\]

由x、y、z为有理数可得：

\[4xy=2, 4xz=3, 4yz=6\]

由于x、y、z在原式中是对称的，所以上式中选择哪个等于2、3、6，都是无所谓的。

三式相乘可得：

\[4^3 \cdot (xyz)^2 = 36\] \[(xyz)^2 = 9/16\] \[xyz = 3/4\]

---

2.设二次函数\(f(x)=ax^2+ax+1\)的图像开口向下，且满足\(f(f(1))=f(3)\)，则\(2a=?\)

解：

令\(y=2a\)，则\(f(1)=2a+1=y+1\)

\[f(f(1))=f(y+1)=f(3)\] \[a(y+1)^2+a(y+1)+1=9a+3a+1\] \[(y+1)^2+(y+1)=12\] \[y^2+3y-10=0\] \[(y+5)(y-2)=0\]

因为图像开口向下，所以\(2a=-5\)。

---

最近，黄冈再次因数学题而火爆网络。

以下是2020黄冈中考数学第16题：

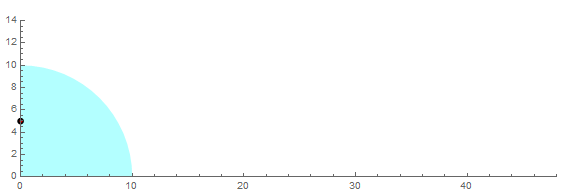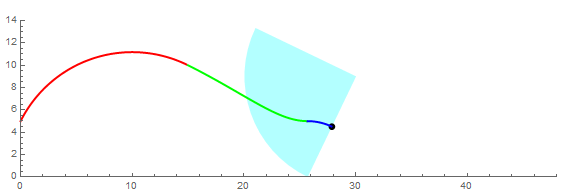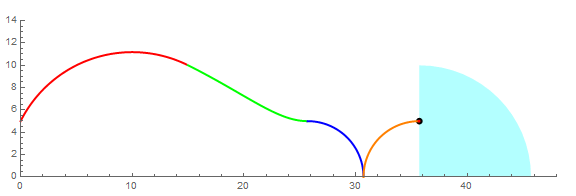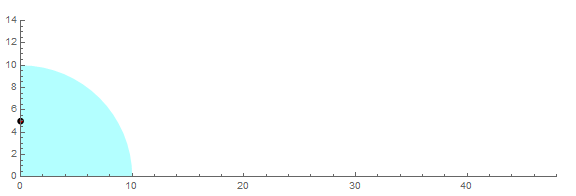
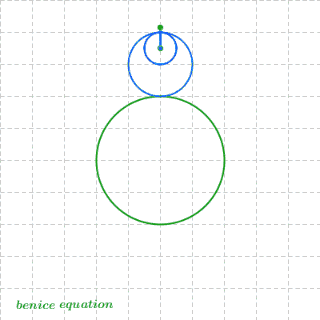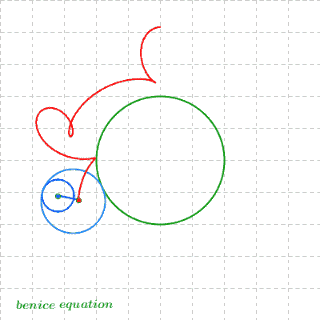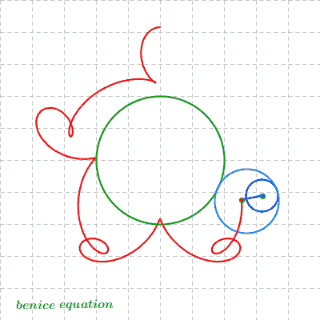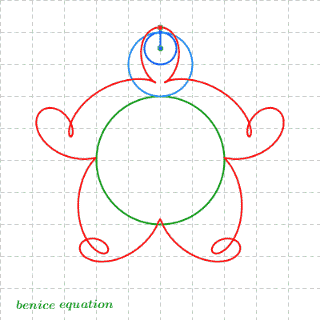
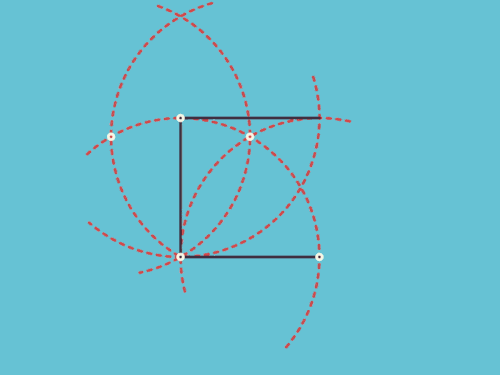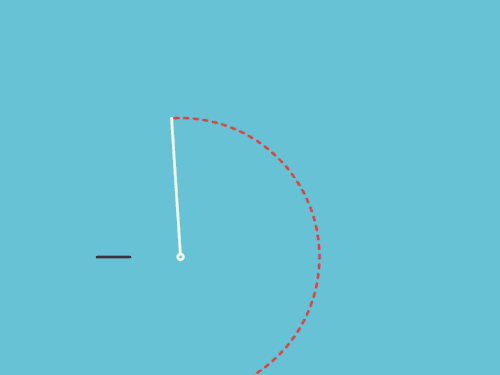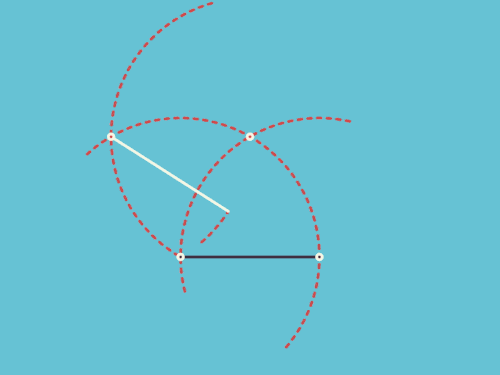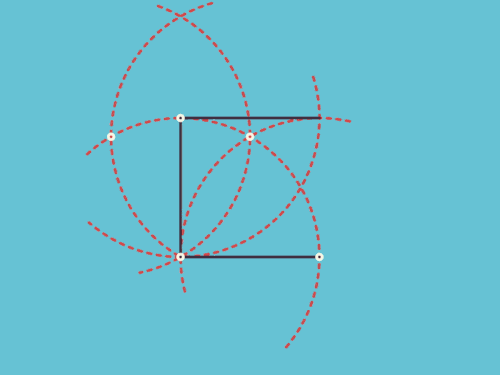
求上图扇形一边的中点P，在扇形滚动一周的过程中，所经历的路径的长度。

显然，第1，3，4段都是圆弧，难就难在第2段（绿色）了。这条曲线可不是那么好求的，普通的本科高数都搞不定它。必须出动椭圆积分才行。

https://www.zhihu.com/question/408523403

如何解答2020黄冈中考数学第16题？

小学能接受1/3这种无限循环小数，初中能接受根号，高中能接受ln(2)，那大学的精确解为什么不能接受椭圆函数。

https://mathworld.wolfram.com/EllipticIntegraloftheSecondKind.html

Elliptic Integral of the Second Kind

这里有个上面动图的GeoGebra版本：

https://github.com/antkillerfarm/antkillerfarm_crazy/blob/master/geogebra/huanggang.ggb

《椭圆函数及其应用》 高本庆 著

---

https://mp.weixin.qq.com/s/FdHstCxJqQ4wYXSRDyqm5A

不敢相信！这份民国时期大学入学考试试卷，竟让170位院士头疼！

玻尔兹曼分布

Boltzmann distribution（又叫Gibbs distribution）本来是脱胎于热力学和统计力学的分布，但在量子力学和机器学习领域也得到了广泛的应用。

Ludwig Eduard Boltzmann，1844～1906，奥地利物理学家，统计力学的奠基人之一。维也纳大学博士，先后执教于格拉茨大学、维也纳大学、慕尼黑大学和莱比锡大学。英国皇家学会会员。

信息熵

设概率实验X有n个可能的独立结局，即n个随机事件\(A_1,\dots,A_n\)，每个随机事件的概率为\(p_1,\dots,p_n\)。则信息熵的定义为：

\[H_n=-k\sum_{i=1}^{n}p_i\ln p_i\tag{1}\]

其中k为一正常数。可以看出\(H_n\)实际上是\(p_i\)的泛函。

以下我们主要从信息熵的角度出发研究玻尔兹曼分布。但不能忽视的是，玻尔兹曼分布最早脱胎于热力学，而信息熵与热力学统计物理中的熵，虽然数学形式一致，但本质是不同的。两者相差一个玻尔兹曼常数。参见：

https://www.zhihu.com/answer/50458123

信息熵与热力学统计物理中的熵有什么区别和联系？

信息熵的定义有多种，公式1给出的是Shannon熵的定义，除此之外还有von Neumann熵、Renyi熵等。以下如无特殊指出，信息熵均指Shannon熵。

参考：

https://mp.weixin.qq.com/s/LGyNq3fRlsRSatu1lpFnnw

机器学习各种熵：从入门到全面掌握

https://mp.weixin.qq.com/s/6I2-5zWbpAUSgoHRUEkj3Q

通俗理解信息熵

最大信息熵原理

事实上，有些随机事件其概率往往不可能直接计算，平常我们对具体问题作出处理时，掌握的仅仅是一些与随机事件有关的随机变量的统计平均值，以及某些其他制约条件。而当一个随机变量的平均值给定时，还可以有多种概率分布与之相容。现在的问题是如何从这些相容的概率分布中挑选出“最可几”的分布来作为实际上的分布。显然，要做到这点，必须有个挑选标准，最大信息熵原理就可作为这种挑选标准。

最可几分布（Most Probable Distribution），又称最概然分布。它表征在特定系统的特定状态下，出现概率最大的分布。从它的定义可以看出，它实际上并不是某种具体的分布，而更像是符合某一特定目标的分布。
比如，麦克斯韦-玻尔兹曼分布、费米-狄拉克分布和玻色-爱因斯坦分布，是热力学常见的三种最可几分布。但它们所处的系统，以及系统的状态各不相同。

基本粒子中所有的物质粒子都是费米子，是构成物质的原材料(如轻子中的电子、组成质子和中子的夸克、中微子)；而传递作用力的粒子(光子、介子、胶子、W和Z玻色子)都是玻色子。

最大熵原理是1957年由E.T.Jaynes提出的，其主要思想是，在只掌握关于未知分布的部分知识时，应该选取符合这些知识但熵值最大的概率分布。其实质就是，在已知部分知识的前提下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断，这是我们可以作出的唯一不偏不倚的选择，任何其它的选择都意味着我们增加了其它的约束和假设，这些约束和假设根据我们掌握的信息无法作出。

Edwin Thompson Jaynes，1922～1998，美国统计学家。普林斯顿大学博士，华盛顿大学教授。

假定系统涉及的M个随机变量\(f_i^{(j)}(j=1,\dots,M)\)的期望值\(F_j\)已知，即：

\[F_j=\sum_{i=1}^{n}f_i^{(j)}p_i\tag{2}\]

其中\(f_i^{(j)}\)表示第j个随机变量在状态i中的取值。\(p_i\)满足归一化条件：

\[\sum_{i=1}^{n}p_i=1\tag{3}\]

将公式2和公式3所述的两个约束，代入公式1，可得如下Lagrange乘子：

\[\begin{array}\\ J(p_i)=H_n/k-\alpha(\sum_{i=1}^{n}p_i-1)-\sum_{j=1}^{M}\beta_j(\sum_{i=1}^{n}f_i^{(j)}p_i-F_j)\\ =-\sum_{i=1}^{n}p_i\ln p_i-\alpha\sum_{i=1}^{n}p_i+\alpha-\sum_{j=1}^{M}\sum_{i=1}^{n}\beta_jf_i^{(j)}p_i+\sum_{j=1}^{M}\beta_jF_j \end{array}\]

对\(p_i\)求导，可得：

\[\frac{\partial J(p_i)}{\partial p_i}=-\ln p_i-1-\alpha-\sum_{j=1}^{M}\beta_jf_i^{(j)}\]

令上式等于0，可得：

\[p_i=\exp(-1-\alpha-\sum_{j=1}^{M}\beta_jf_i^{(j)})\tag{4}\]

公式4就是一般情况下的最大信息熵公式。

相关名词辨析

这里有三个非常容易混淆的名词需要解释。

Maxwell–Boltzmann statistics是研究热平衡状态下无相互作用的物体粒子的能量均值分布的统计学分支。

Boltzmann distribution表征一个包含各种能量状态的系统中粒子的概率分布。

Maxwell-Boltzmann distribution表征粒子的能级和速度的分布。

简而言之，Maxwell–Boltzmann statistics是基于特定假设的统计学分支。而后两者则是具体情况下的概率分布。

与Maxwell–Boltzmann statistics相对应的概念是Bose–Einstein statistics和Fermi–Dirac statistics。后两者分别对应玻色子和费米子的热力学统计。

参考：

https://en.wikipedia.org/wiki/Maxwell–Boltzmann_statistics

https://en.wikipedia.org/wiki/Boltzmann_distribution

https://en.wikipedia.org/wiki/Maxwell–Boltzmann_distribution

玻尔兹曼分布的推导

Maxwell–Boltzmann statistics研究的对象是一个由N（N很大）个微观粒子组成的近独立体系，体系的总能量E等于各个粒子能量之和。通常微观粒子的状态和能量是量子化的（即所谓能级），每一能级上又具有若干个量子态。为此，可引入下列符号：

名称	符号
单粒子状态编号	\(1,\dots,n\)
能级	\(E_1,\dots,E_n\)
量子态数	\(g_1,\dots,g_n\)
微观粒子数	\(N_1,\dots,N_n\)

令\(m=g_1+\dots+g_n\)，\(p_s\)为任何一个确定的微观粒子处于第s个量子态上的概率。因此，相应的信息熵和概率分布的归一化条件为：

\[H_m=-k\sum_{s=1}^{m}p_s\ln p_s\tag{5}\] \[\sum_{s=1}^{m}p_s=1\tag{6}\]

由于N是个大数，可以认为第s个量子态上的微观粒子数为\(N_s=Np_s\)，体系的总能量为：

\[E=\sum_{s=1}^{m}E_sN_s=\sum_{s=1}^{m}E_sNp_s\tag{7}\]

和公式4的推导过程类似，Maxwell–Boltzmann statistics条件下的信息熵最大值的概率分布为：

\[p_s=\exp(-1-\alpha-\beta E_s)\tag{8}\]

由\(p_s\)的归一化条件可得：

\[p_s=\frac{1}{Z}e^{-\beta E_s}\tag{9}\]

其中：

\[Z=\sum_{s=1}^{m}e^{-\beta E_s}\]

于是，当体系处于热平衡状态时，第s个量子态上的粒子数可表为：

\[N_s=Np_s=\frac{N}{Z}e^{-\beta E_s}\tag{10}\]

考虑到同一单粒子能级\(E_i\)上的\(g_i\)个量子态均具有相同的能量\(E_i\)，因此：

\[N_i=N_sg_i\tag{11}\]

由气体分子的速度分布可得：

\[\beta=\frac{1}{kT}\tag{12}\]

其中，k是Boltzmann常数，T是热力学温度。

将公式11、12代入公式10可得：

\[N_i=\frac{Ng_ie^{-E_i/kT}}{\sum_{i=1}^{n}g_ie^{-E_i/kT}}\]

上式就是Boltzmann distribution的PDF。