math » 数学狂想曲(二)——傅立叶变换, DFT, 拉普拉斯变换
2016-12-15 :: 6299 Words欧拉公式
参考(续)
https://mp.weixin.qq.com/s/vdxfzuGEMoiwGARYYzXbKg
最伟大的数学公式:欧拉公式
https://mp.weixin.qq.com/s/cy5U6in3QQSy7yAXkDjvqA
欧拉:1分钟解决\(e^\pi\)和\(\pi^e\)谁大的问题!
https://mp.weixin.qq.com/s/G7eZMTQbQZBjJf4HfDk21A
虚数到底有什么意义?从i说起
傅立叶变换
正弦波的叠加(傅立叶级数):
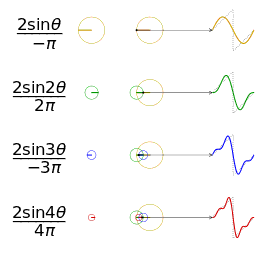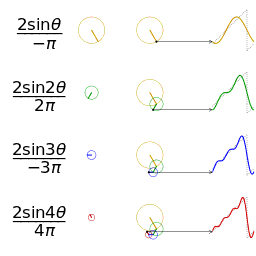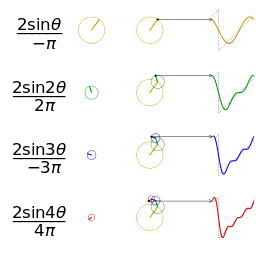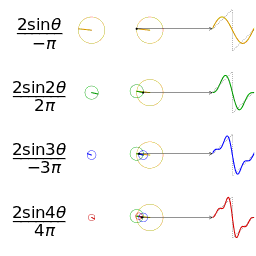
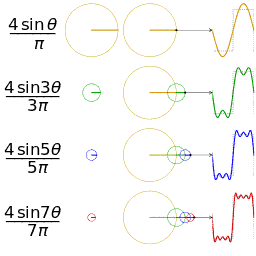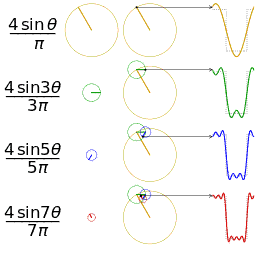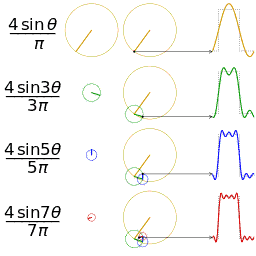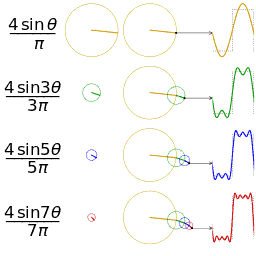
时域、频域、相位:
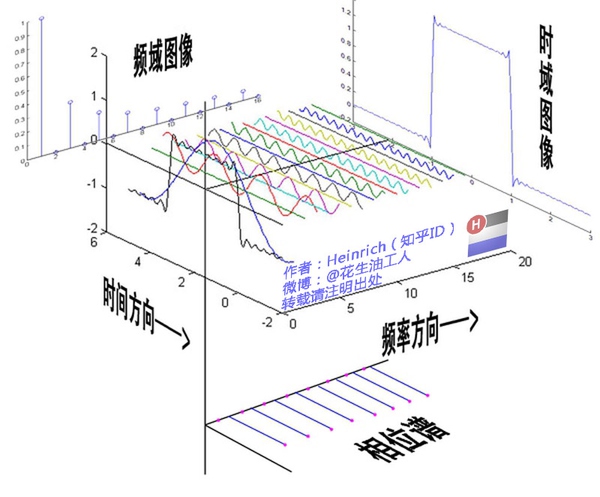
周期为T的函数可展开为:
\[f(t)=a_0+\sum_{n=1}^{\infty}\left(a_n\cos(\frac{2\pi n}{T}t)+b_n\sin(\frac{2\pi n}{T}t)\right)\tag{1}\]公式1被称为函数的傅立叶展开式(Fourier expansion)。这里是傅立叶展开式的三角形式,后面还有复指数形式。
令\(\omega=\frac{2\pi}{T}\),则公式1可改写为:
\[f(t)=a_0+\sum_{n=1}^{\infty}\left(a_n\cos(n\omega t)+b_n\sin(n\omega t)\right)\tag{2}\]这里的\(\omega\)被称作角速度(Angular Velocity)。而这里的\(a_n,b_n\)则被称为傅立叶级数(Fourier series)。
对公式2两边进行积分:
\[\begin{align} \int_{-\pi}^{\pi}f(t)\mathrm{d}t&=\int_{-\pi}^{\pi}A_{0}\mathrm{d}t+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty}{[a_{n}cos(n\omega t)+b_{n}sin(n\omega t)]}\mathrm{d}t\\ &=\int_{-\pi}^{\pi}A_{0}\mathrm{d}t+0=2\pi A_{0} \end{align}\] \[A_{0}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(t)\mathrm{d}t\]类似的:
\[\begin{align} a_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)cos(n\omega t)\mathrm{d}t\\ b_{n}=\frac{2}{T}\int_{t_{0}}^{t_{0}+T}f(t)sin(n\omega t)\mathrm{d}t\\ \end{align}\]将欧拉公式的两个变种:
\[cos(\theta)=\frac{e^{i\theta}+e^{-i\theta}}{2}, sin(\theta)=\frac{e^{i\theta}-e^{-i\theta}}{2i}=-i\cdot \frac{e^{i\theta}-e^{-i\theta}}{2}\]代入公式2:
\[\begin{align} f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}{[a_{n}\frac{e^{in\omega t}+e^{-in\omega t}}{2}-ib_{n}\frac{e^{in\omega t}-e^{-in\omega t}}{2}]}\\ =\frac{a_{0}}{2}+\sum_{n=1}^{\infty}{[\frac{a_{n}-ib_{n}}{2}e^{in\omega t}+\frac{a_{n}+ib_{n}}{2}e^{-in\omega t}]}\\ \end{align}\]将\(a_n,b_n\)代入:
\[f(t)=\frac{1}{T}\sum_{n=-\infty}^{+\infty}\int_{t_{0}}^{t_{0}+T}f(t)e^{-in\omega t}\mathrm{d}t\cdot e^{in\omega t}\]上式为Fourier expansion的复指数形式。
令
\[F_n=\frac{1}{T}\int_{t_{0}}^{t_{0}+T}f(t)e^{-in\omega t}\mathrm{d}t\]则:
\[f(t)=\sum_{n=-\infty}^{+\infty} F_n e^{in\omega t}\tag{3}\]这里的\(F_n\)被称为复振幅。
傅立叶的时代,电学尚不成熟,因此傅立叶级数的落脚点实际上是求解热传导方程,这也就是求解偏微分方程的分离变量法。
https://zhuanlan.zhihu.com/p/131385010
偏微分方程-热传导方程及连续性方程的导出
https://zhuanlan.zhihu.com/p/138032373
偏微分方程基础——分离变量法
傅立叶级数与傅立叶变换:
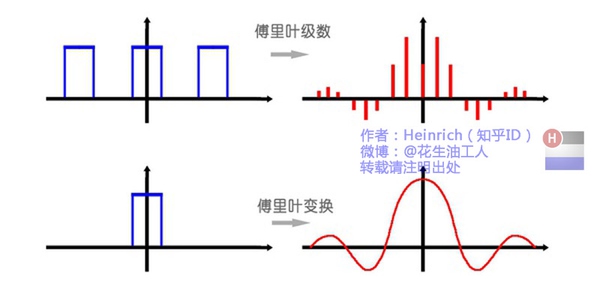
傅立叶级数针对的是周期函数。对于非周期函数,也就是\(T\to \infty\)的函数,需要有一些特殊的处理。
从公式3可以看出如果\(T\to \infty\),则\(F_n\to 0\),但\(F_nT=\frac{2\pi F_n}{\omega}\)可望趋于有限值。我们定义:
\[F(i\omega)=\lim_{T\to \infty}\frac{2\pi F_n}{\omega}\]因为:
\[f(t)=\sum_{n=-\infty}^{+\infty} F_n e^{in\omega t}=\sum_{n=-\infty}^{+\infty}\frac{F_n}{\omega}e^{in\omega t}\cdot \omega\]又因为:
\[\text{if }T\to \infty, \text{then }\frac{F_n}{\omega}\to \frac{F(i\omega)}{2\pi}, \omega\to \mathrm{d}\omega, n\omega \to \omega\]所以:
\[F(i\omega)=\int_{-\infty}^{+\infty}f(t)e^{-i\omega t}\mathrm{d}t\tag{4}\] \[f(t)=\lim_{T\to \infty}\sum_{n=-\infty}^{+\infty}\frac{F_n}{\omega}e^{in\omega t}\cdot \omega=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(i\omega)e^{i\omega t}\mathrm{d}\omega\tag{5}\]公式4为傅立叶变换,公式5为傅立叶逆变换(inverse Fourier transform)。
欧拉公式:
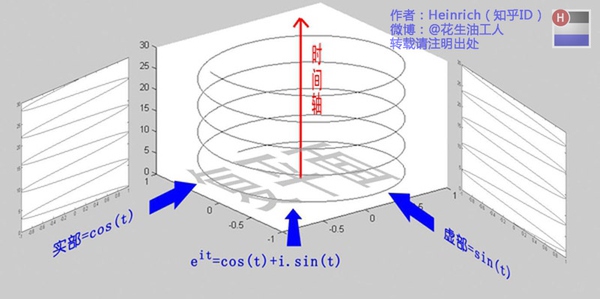
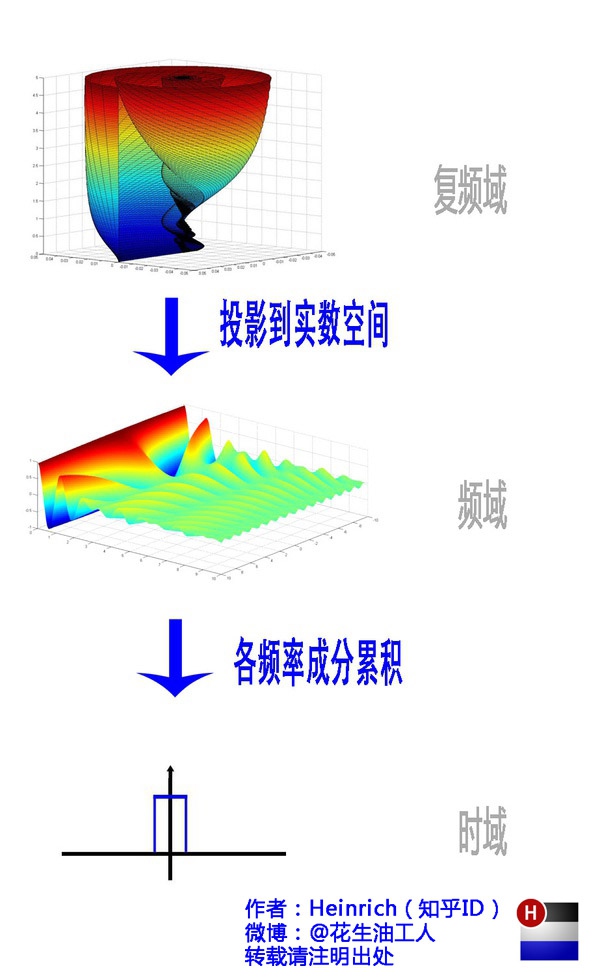
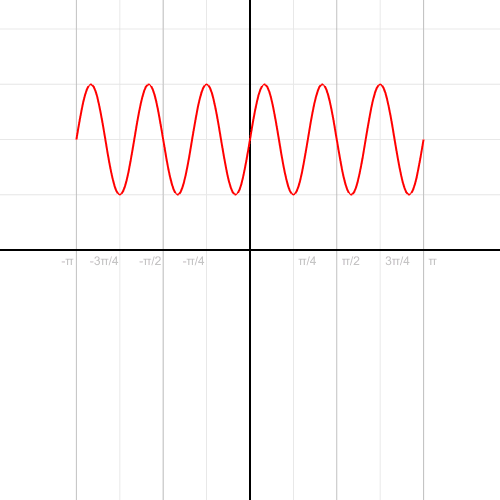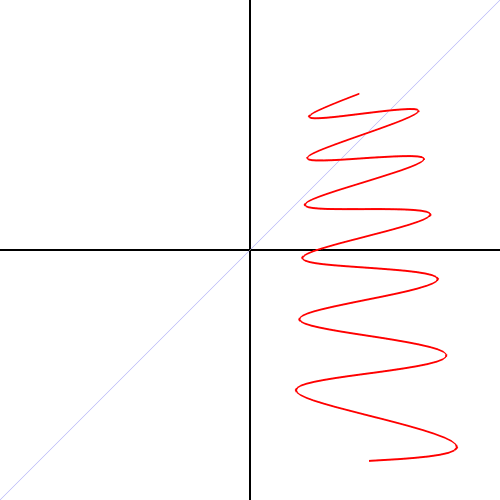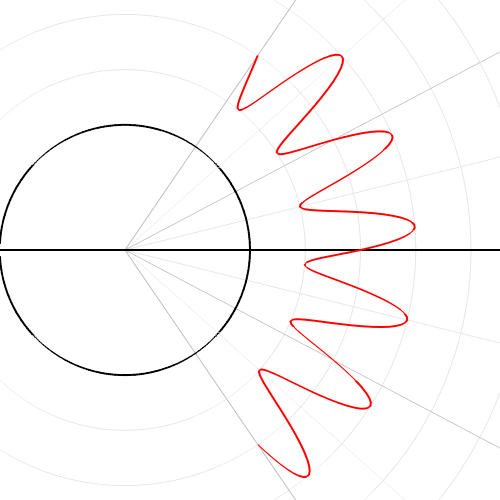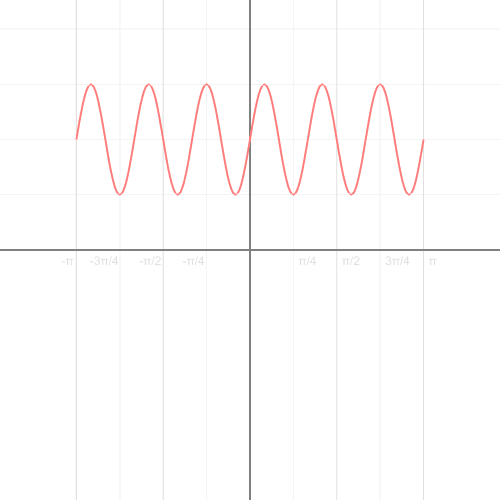
欧拉公式所描绘的,是一个随着时间变化,在复平面上做圆周运动的点,随着时间的改变,在时间轴上就成了一条螺旋线。如果只看它的实数部分,也就是螺旋线在左侧的投影,就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。
正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。
参考:
https://www.zhihu.com/question/21665935
傅立叶级数和傅立叶变换是什么关系?
https://zhuanlan.zhihu.com/p/19763358
傅立叶分析之掐死教程
https://zhuanlan.zhihu.com/p/41455378
傅立叶级数的推导
https://zhuanlan.zhihu.com/p/41875010
傅立叶变换的推导
https://zhuanlan.zhihu.com/p/75521342
离散傅立叶变换(DFT)
https://mp.weixin.qq.com/s/4wv8fYe8pahnt-301t-3Hw
傅立叶变换
https://mp.weixin.qq.com/s/MLe_MtQE27rZTncaQeU4cg
论频谱中负频率成分的物理意义
https://mp.weixin.qq.com/s/TEtZbh0NHSemgWQlrgo2Vw
傅立叶变换还能这么玩
https://bl.ocks.org/jinroh/7524988
Fourier series visualisation with d3.js
https://mp.weixin.qq.com/s/OEo0aboqxQ42ZfMFACXQPw
信号与系统公式大全(傅立叶变换、拉普拉斯变换、Z变换、卷积…)
https://mp.weixin.qq.com/s/57WKK0xEBti9BjUD1xVlRQ
手把手教你编写傅立叶动画
https://mp.weixin.qq.com/s/gYpT_cLcxy6xJ5nww-Obqw
一文读懂傅立叶变换处理图像的原理
https://mp.weixin.qq.com/s/vzXejSzH9rzvhfYJEYSyrQ
傅立叶变换有什么用
https://www.zhihu.com/question/279808864
为什么傅立叶变换可以把时域信号变为频域信号?
DFT
FT针对的是连续信号,但数字信号处理只能处理离散数据,于是就有了Discrete-time Fourier transform(DTFT):
\[X_{2\pi}(\omega) = \sum_{n=-\infty}^{\infty} x[n] \,e^{-i \omega n}\]由于采样频率是有限的,由Nyquist采样定理可知,DTFT是个周期函数,因此我们取它的一个周期即可,这就是所谓的DFT:
\[\begin{align} X_k &= \sum_{n=0}^{N-1} x_n\cdot e^{-\frac {2\pi i}{N}kn}\\ &= \sum_{n=0}^{N-1} x_n\cdot [\cos(2 \pi k n / N) - i\cdot \sin(2 \pi k n / N)], \end{align}\]这里的\(x_n\)和\(X_k\)都是长度为N的复数序列。
对于实数序列而言,我们有如下性质:
\[x^*(n) = x(n), X^*(n) = X(N - n)\]因此,用N/2长度的序列\(X_k\)就足以表示Real DFT的结果。

必须注意的是:Real DFT的结果仍然是复数。
参考:
https://www.zhihu.com/question/23137926
DFT与DTFT区别是什么?
http://www.dspguide.com/ch12/1.htm
Real DFT Using the Complex DFT
http://blog.miskcoo.com/2018/01/real-dft
实序列离散傅立叶变换的快速算法
拉普拉斯变换
\[F(s) =\int_0^{+\infty} e^{-st} f(t)\mathrm{d}t,s = \sigma + i \omega \tag{1}\]傅立叶变换的收敛有一个狄利克雷条件,要求信号绝对可积/绝对可和。
为了使不满足这一条件的信号,也能读出它的“频率”,可以采用拉普拉斯变换和Z变换。它们对“频率”的含义做出了扩充,使得大多数有用信号都具有了对应的“频率”域表达式。
拉普拉斯变换(Laplace transform)将频率从实数推广为复数,因而傅立叶变换变成了拉普拉斯变换的一个特例。当s为纯虚数时,\(x(t)\)的拉普拉斯变换,即为\(x(t)\)的傅立叶变换。
从图像的角度来说,拉普拉斯变换得到的频谱是一个复平面上的函数。
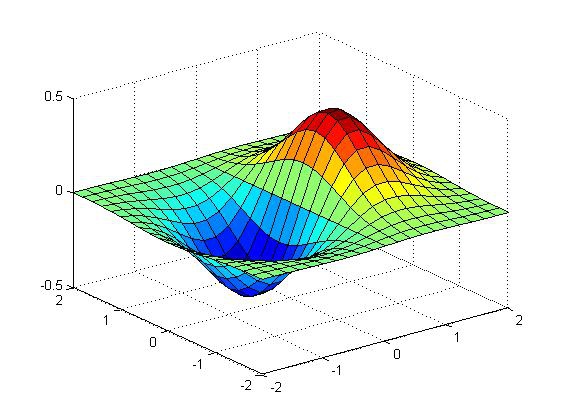
而傅立叶变换得到的频谱,则是从虚轴上切一刀,得到的函数的剖面。
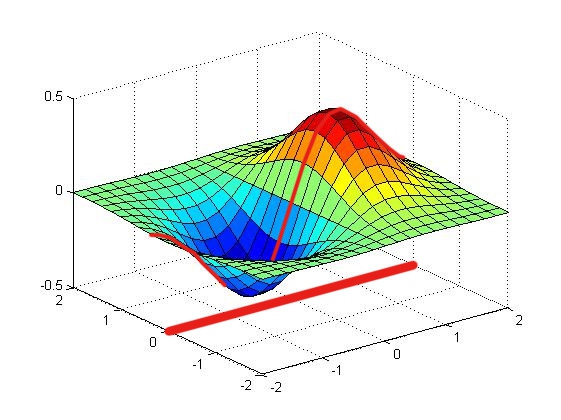
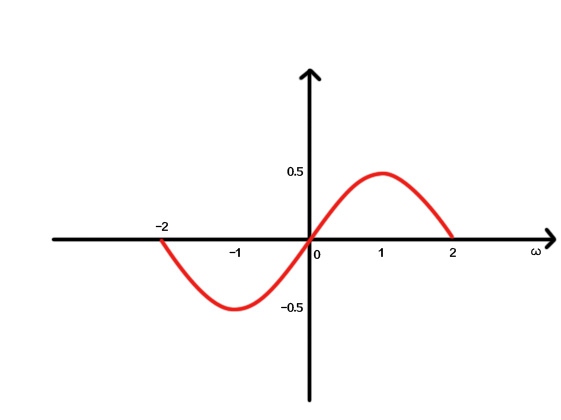
由复数的指数表示\(z=re^{i\theta}\)可知,复频域可以看作是普通频域(r)+相位谱(\(\theta\))。
此外,傅立叶变换和拉普拉斯变换之所以在计算上比较方便,还在于指数函数正好是线性微分方程的特征函数。
由于一阶微分方程\(\frac{\mathrm{d}y}{\mathrm{d}t}=\lambda y\)的解是\(e^{\lambda t}\)。由线性代数中的特征向量可类比得到,\(e^{\lambda t}\)是线性微分方程的特征函数,从而可以将线性微分方程转换为线性方程。
公式1的另一个值得注意的地方是:它的积分范围是\([0, +\infty)\)。这样的变换一般被称为Unilateral Laplace transform或者One-sided Laplace transform,也就是通常意义下的Laplace transform。
如果它的积分范围是\((-\infty, +\infty)\)的话,那就是Two-sided Laplace transform了。
容易看出,复数域的Fourier transform和Two-sided Laplace transform是等价的,而Unilateral Laplace transform是前两者的特例,实数域的Fourier transform又是Unilateral Laplace transform的特例。
Laplace transform的积分范围不是随便定的,它隐含了Causality条件:当系统的输出仅与当前的输入或者过去的输入有关,那么这个系统就是causal的。
想看清楚这一点也不难:用-t替换t,然后积分范围就变成了\((-\infty, 0]\)。
我们还可以换一个角度看待Laplace transform和Fourier transform。
绝对可积条件限制了Fourier transform的应用范围,而不满足绝对可积条件的函数,通常在\(\infty\)处的值是\(\infty\)。一个自然的思路是给这样的函数\(f(x)\),除以一个缩放的系数。显然只有比\(f(x)\)更高阶的函数,才能在\(\infty\)处将函数值约束在一个有限的范围内。
\(e^x\)就是个很合适的选择,它的增长速度超过了多数的常见函数。
参考:
https://www.zhihu.com/question/22085329
傅立叶变换、拉普拉斯变换、Z变换的联系?为什么要进行这些变换。研究的都是什么?
https://www.zhihu.com/question/23280174
矩阵,数列,微分方程的特征值是什么关系?
https://mp.weixin.qq.com/s/ObYF_kMBvBdz4djdT7G77w
傅立叶变换和拉普拉斯变换的物理解释及区别
https://www.zhihu.com/question/33177784
解微分方程为什么会出现个e?
https://mp.weixin.qq.com/s/v07bgw90WDonyZQuuoWozA
8张动图,让您秒懂什么是电压电流的超前与滞后!
https://mp.weixin.qq.com/s/cR3k5-looApwD01ZzgixSw
关于Fourier和Laplace
https://zhuanlan.zhihu.com/p/311886981
微分方程VS机器学习,实例讲解二者异同

您的打赏,是对我的鼓励
