math » 数学狂想曲(一)——搞笑图片的数学原理, 欧拉公式
2016-11-27 :: 5106 Words搞笑图片的数学原理

这是一个在各论坛流传已久的图片。这个题目的描述虽不复杂,但仅凭大学本科的高等数学,实际上是搞不定这个问题的。
首先需要明确的是,上图中的被积函数\(\frac{1-\cos x}{x^2}\)的原函数不是初等函数,因此无法使用牛顿-莱布尼茨公式,求解该积分值。
它的解法其实图片中已经给出了线索,那就是傅立叶变换的能量积分公式。
以下是推导步骤:
由半角公式:
\[2\sin^2\frac{x}{2}=1-\cos x\]可得:
\[\frac{1-\cos x}{x^2}=\frac{2\cdot\sin^2\frac{x}{2}}{4\cdot\frac{x^2}{4}}=\frac{1}{2}\left(\frac{\sin\frac{x}{2}}{\frac{x}{2}}\right)^2\]查常用函数的傅立叶变换表,可得:
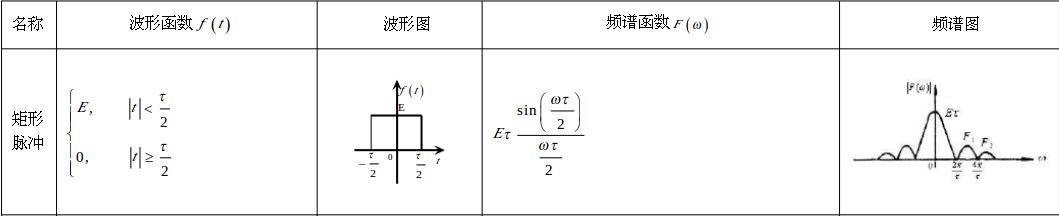
代入能量积分公式,可得:
\[\int_{-\infty}^{+\infty}\left(\frac{\sin\frac{x}{2}}{\frac{x}{2}}\right)^2\mathrm{d}x=2\pi\int_{-\infty}^{+\infty}(rect(t))^2\mathrm{d}t=2\pi\cdot 1\]因此:
\[\int_{-\infty}^{+\infty}\frac{1-\cos x}{x^2}\mathrm{d}x=\frac{1}{2}\cdot 2\pi=\pi\]实际上,这类积分都是Dirichlet积分的变种,解法也不止一种。
参见:
http://wenku.baidu.com/view/bb9c8ffe910ef12d2af9e71a.html
关于Dirichlet积分的十种计算方法
http://wenku.baidu.com/view/1b47c415cc7931b765ce1547.html
常用函数傅立叶变换表
下面回到原题,何为“能量积分”呢?
由电学的功率公式和欧姆定理可得:
\[W=UI=\frac{U^2}{R}=I^2R\]可见,无论\(f(t)\)表示电压U,还是表示电流I,\([f(t)]^2\)都和功率成正比,即\(\int[f(t)]^2\mathrm{d}t\)和能量成正比。
傅立叶变换的能量积分公式的物理意义是:同一信号的时域能量积分等于它的频域能量积分。通俗的说就是一个信号的能量,既可以看作是一段时间内信号能量的总和,也可看作是该信号各个频率分量的能量总和。
在历史上,该公式由Marc-Antoine Parseval于1799年发现,最初主要用于研究复变函数,后来才应用到傅立叶变换和信号处理领域。
它的更一般的描述为:一个信号所含有的能量(功率)恒等于此信号在完备正交函数集中各分量能量(功率)之和。
Marc-Antoine Parseval des Chênes,1755~1836,法国数学家。曾5次参选法国科学院院士,但都落选了。
欧拉公式
由于欧拉大神的贡献很多,数学上以其命名的公式也有很多,而且知名度都不低。日常使用时,如果不以领域做区分,人们根本就不知道谈论的是哪个欧拉公式。
这里主要讨论复变函数领域的基石——欧拉公式:
\[e^{ix}=\cos x + i \sin x\]自然对数e
在讨论欧拉公式之前,首先要理解一下自然对数e的含义。
推荐阅读以下文章:
https://www.zhihu.com/answer/29370489
数学里的e为什么叫做自然底数?是不是自然界里什么东西恰好是e?
这里对上文中的要点做一个摘要。
假设你在银行存了1元钱(下图蓝圆),很不幸同时又发生了严重的通货膨胀,银行存款利率达到了逆天的100%!
银行一般1年才付一次利息,根据下图,满1年后银行付给你1元利息(绿圆),存款余额=2元
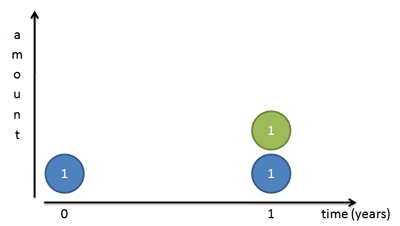
银行发善心,每半年付利息,你可以把利息提前存入,利息生利息(红圆),1年存款余额=2.25元
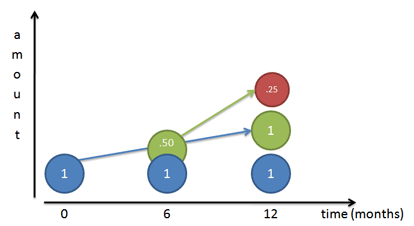
假设银行超级实在,每4个月就付利息,利息生利息(下图红圆、紫圆),年底的余额≈2.37元
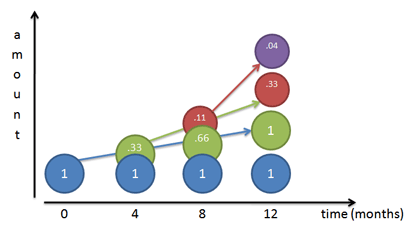
假设银行人品爆发,一年365天,愿意天天付利息,这样利滚利的余额≈2.71456748202元
假设银行丧心病狂的每秒付利息,你也丧心病狂的每秒都再存入,1年共31536000秒,利滚利的余额≈2.7182817813元
这个数越来越接近于e了!
哎呀!费了半天劲也没多挣几个钱啊!
对!1元存1年,在年利率100%下,无论怎么利滚利,其余额总有一个无法突破的天花板,这个天花板就是e,即:
\[e=\lim_{n\to\infty} \left( 1 + \frac{1}{n} \right)^n\]自然对数的研究历史
上面例子的体例,和现行教科书类似,都是直接以极限方式定义e。然而,这并不是自然对数在历史上的研究路径。
从利息出发的复利计算,或者说求高次幂运算,在历史上催生了最早的对数表(1614年)。然而,这个问题本身和e并无直接关联,使用常用对数同样可以求解复利问题。
真正催生自然对数e的是对数表的编制过程。
对于那时期的人们来说,编制对数表是件巨大的工程,常需要花费数学家数年,甚至数十年的时间。
在大量的实践中,人们发现采用\(\left( 1 + \frac{1}{n} \right)^n,n \gg 0\)为底,可以很大程度的节省计算量。
事实上,最早的几个对数表的作者中,纳皮尔采用\(\left( 1 + \frac{1}{10^7} \right)^{10^7}\)的倒数为底,而比尔吉采用\(\left( 1 + \frac{1}{10^4} \right)^{10^4}\)为底。这两个数分别是\(\frac{1}{e}\)和e的近似值。
从e到欧拉公式
早期的对数表作者虽然已经不自觉的享受e的好处,然而他们并没有明确发现或定义e。
e的定义有赖于微积分的发展。
十七世纪上半叶是微积分的萌芽时期,也可称为前牛顿-莱布尼茨时期。这里所提到的数学家,实际上只比牛顿、莱布尼茨,早一到两代人。
比如费马(Pierre de Fermat)在1636年之前,就知道:
\[\int_0^ax^n\mathrm{d}x=\frac{a^{n+1}}{n+1},n\neq -1\]于是人们自然会去思考:
\[\int_0^a\frac{1}{x}\mathrm{d}x=?\tag{1}\]两个耶稣会教士Grégoire de Saint-Vincent和Alphonse Antonio de Sarasa发现:
\[\int_0^a\frac{1}{x}\mathrm{d}x=k \log y\]这个发现表明,\(y=\frac{1}{x}\)曲线下的面积和y的对数成正比。
William Oughtred认为,如果采用合适的数为底的话,就可以约去比例因子k。从而上式可变为:
\[\int_0^a\frac{1}{x}\mathrm{d}x=\ln x\]他将这样形式的对数,称为自然对数。这实际上就是\(\left( 1 + \frac{1}{n} \right)^n\)节省计算量的原因。
William Oughtred,1575~1660,英国数学家。他对数学符号的发展产生很大的影响,现行的大于、小于符号就是他的发明。
到了John Bernoulli时代,积分问题扩展到如下形式:
\[\int\frac{\mathrm{d}x}{ax^2+bx+c}\tag{2}\]显然,这类问题可以通过配方换元法,转换成公式1的形式。然而,其中的要害在于,求解方程\(ax^2+bx+c=0\),而这个方程的解,有可能为复数。
出于解方程的需要,John Bernoulli系统研究了\(\lim_{n\to\infty} \left( 1 + \frac{1}{n} \right)^n\)的性质,并认为它是一个重要的常数。这个思想明显影响了他的学生Euler。
除此之外,在求解公式2的特例:
\[\frac{\mathrm{d}x}{b^2+x^2}\tag{3}\]John Bernoulli发现,可以令\(x=\sqrt{-1}b(t-1)/(t+1)\),从而上式变为:
\[\frac{-\mathrm{d}t}{\sqrt{-1} \cdot 2bt}\tag{4}\]公式3的积分是\(\arctan\),而公式4的积分是一个虚数的对数。利用这种方法,可以建立三角函数和虚数对数之间的关系。
这里需要指出的是,John Bernoulli对于复数的理解仍停留在Cardano的水平,这里的虚数对数和后面提及的复数指数、复数对数在内涵上是不同的,仅仅是种解方程的技巧而已。
1740年,Euler发现\(y=2\cos x\)和\(y=e^{\sqrt{-1}x}+e^{-\sqrt{-1}x}\)是同一个微分方程的解,因此它们应该相等。
1743年,Euler进一步指出:
\[\cos x=\frac{e^{\sqrt{-1}x}+e^{-\sqrt{-1}x}}{2},\sin x = \frac{e^{\sqrt{-1}x}-e^{-\sqrt{-1}x}}{2\sqrt{-1}}\]最后,在1748年,Euler指出:
\[e^{ix}=\cos x + i \sin x\]虚数符号i虽然也是Euler的发明,但那是1777年以后的事情了。这里用的是现代的表示方法。
这个结果最早是Roger Cotes于1714年发现的,Euler算是重新发现。
从牛顿到John Bernoulli、Euler,无穷数列成为当时数学家的一项工具。上述等式中很多都是基于函数的无穷数列展开式的性质得出的。
但与现在主要采用泰勒展开式不同,当时更知名的展开公式是牛顿发明的二项式定理,泰勒展开式用的并不多。
复变Euler公式
Euler时代,人们虽然对于复数的性质做了颇多的探索,但仍难以逃脱“复数是解方程的技巧”的束缚。这主要体现在两个方面:
1.尽管Euler晚年已经有复平面的概念,但他对复数的几何意义研究甚少。在他看来,为复数这种因解代数方程而引入的技巧,提供一种几何解释,是一件不太自然的事情。
2.复数的实部和虚部是分开处理的,用途局限于求解实变量微积分。最典型的例子就是,Euler时代的Euler公式,其自变量x是实数。
之后,随着复平面、复数的向量表示逐渐被人接受,人们开始倾向于接受复数是一种数,而不仅仅是一种解方程的技巧。
在复数的系统化中,做出最大贡献的,当属Augustin-Louis Cauchy。
具体到Euler公式,Cauchy针对复变函数的特性,定义了如下规则:
\(f(z)\)为一复变函数,且满足:
1.\(f(z)\)在复平面内处处解析。
2.\(f'(z)=f(z)\)。
3.当\(Im(z)=0\)时,\(f(z)=e^x\),其中\(x=Re(z)\)。
最终符合这一条件的函数为:
\[e^x(\cos y + i \sin y)\]因此,复变Euler公式为:
\[e^z=e^x(\cos y + i \sin y)\]可见,与原始的Euler公式不同,复变Euler公式不是证明出来的,而是定义出来的。
总结
1.Cardano解三次方程发明虚数。
2.高次幂运算催生对数表。
3.对数表的编制过程中,发现了e。
4.Euler根据无穷数列展开式,发现Euler公式。
5.Cauchy定义了复变Euler公式。
参考:
《古今数学思想》
《不可思议的e》
Other
正文的考古工作到此结束,下面写一些相关的冷知识。
\[e^i=\lim_{n\to\infty} \left( 1 + \frac{i}{n} \right)^n\]如果\(e^{i\theta}\)表示幅角为\(\theta\)的单位向量,那么\(e^{i\omega t}\)就表示角速度为\(\omega\)的旋转单位向量。
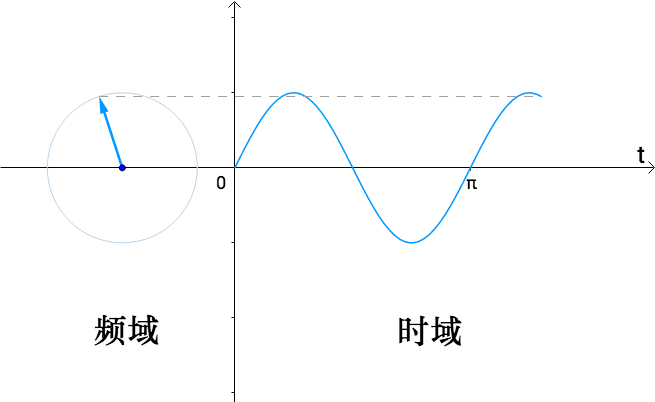
参考
https://mp.weixin.qq.com/s/kwfA7CqBz1myyUR3NBKp1g
虚数i是真实存在的吗?
https://mp.weixin.qq.com/s/4fccUusfRQ7KYhIKWVy38w
如何用图示来优雅地解释复数的意义?

您的打赏,是对我的鼓励
