• Polyhedral Model
  • 教程
  • 笔记

Polyhedral Model

教程

Polyhedral Model的内容主要在《编译原理》（龙书）第十一章——并行和局部优化。

《多面体编译理论与深度学习实践》 赵捷 李宝亮著

https://www.cs.colostate.edu/~pouchet/

888.11-Polyhedral Compilation Foundations

https://polyhedral.info/

一个Polyhedral方面的社区，有大量资料

---

Integer Set Library（ISL）：一个用于操作由线性约束条件约束的整数点的集合和关系的库。主要作为实现Polyhedral Compilation的数学工具库。

官网：

https://libisl.sourceforge.io/

ISL的python接口库：

https://documen.tician.de/islpy/index.html

笔记

基于多面体模型的编译优化技术代表了程序自动并行化领域众多方向最先进的水平,成为国际上多个编译研发团队的研究热点。

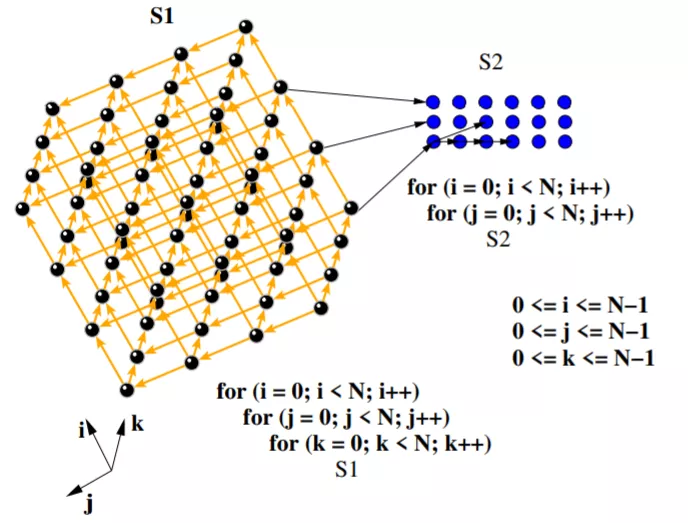
多面体模型(Polyhedral)主要关注的是程序设计中的循环优化，两层循环的循环变量的取值范围可以构成一个平面，三层循环的循环变量可以组成一个长方体，如上图所示，因此得名多面体模型。

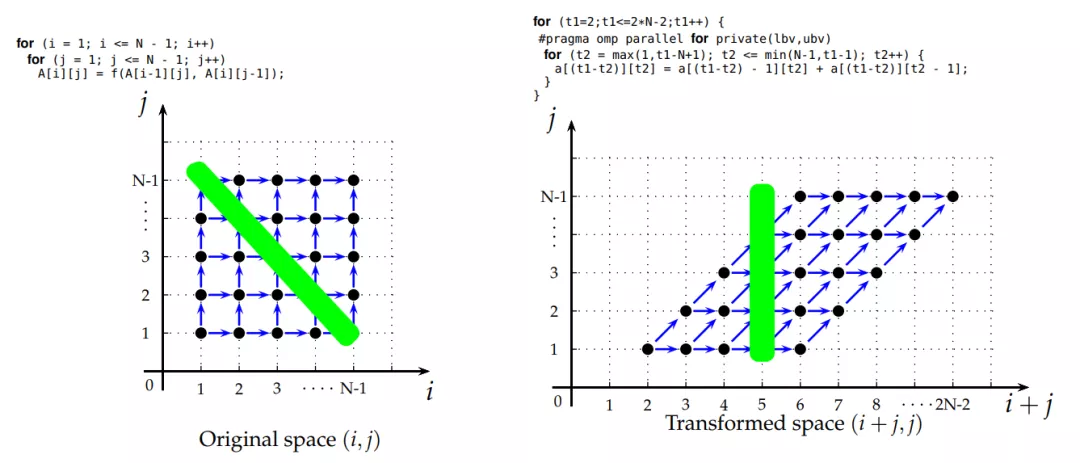
多面体编译优化关注的是在确保程序执行正确的前提下重组循环的结构，实现性能最佳。上图左边表示的原始的二维迭代空间，蓝色箭头表示数据（黑点）之间存在依赖关系，对角线的绿色表示数据没有依赖关系，经过变基操作之后变为右图的表达式及迭代空间，从形状看像是把多面体进行了变形，形象地体现出多面体优化的过程。

---

Polyhedral Model在传统的CPU/GPU编译器领域已经有非常多的实践。

比如gcc中的Graphite：

http://gcc.gnu.org/wiki/Graphite

论文：

GRAPHITE: Polyhedral Analyses and Optimizations for GCC

还有LLVM中的polly：

https://polly.llvm.org/

LLVM Framework for High-Level Loop and Data-Locality Optimizations

---

计算图优化

算子优化

指令优化

---

循环不变量外提

循环展开，软流水，并行化，向量化

向量化：标量运算转换为向量运算，并在同一硬件上执行。优点：Cache命中率高。

并行化：将任务拆分成多个可并行执行的子任务，并同时在多个硬件单元上执行。优点：降低同步和通信开销。

向量化和并行化通常是两个冲突的优化目标，前者通常在内层循环进行，而后者通常在外层循环进行。

---

并行性发掘

从app角度可以分为：数据级并行和任务级并行。

从实现角度可分为：

• 指令级并行。
• 单指令多数据并行。
• 线程级并行。
• 请求级并行。

---

Loop tiling：将大块循环迭代拆解为若干小块的循环迭代，减少数据重用的周期。

Loop fusion：将多个具有“生产-消费”关系的循环块合并到一起，减少中间数据的搬运。

这也是两个冲突的目标，Loop fusion会导致Loop tiling的约束复杂化。

https://blog.csdn.net/wangbowj123/article/details/101173269

循环优化与多面体模型

---

线性变换（linear transformation）：\(y=Ax\)

仿射变换（affine transformation）：\(y=Ax+b\)

迭代空间（iteration space）：在一些计算过程中动态执行示例的集合，也就是各个循环下标的取值的组合。

数据空间（data space）：被访问的数组元素的集合。

处理器空间（processor space）：系统中处理器的集合。通常情况下，这些处理器使用整数或者整数向量进行编号。

因为循环是多重的，所以iteration space是个多面体。同样的，数据是多维的，它也是一个多面体。

从ALU到core，到die，到chip；从register到L0 Cache，到L1 Cache，到RAM；无论是运算器，还是存储器，都是一个有层次的结构，这也是一个多面体。

由于非线性数学理论的不完备，目前的Polyhedral Model主要研究仿射变换。在这个前提下，人们发现不同space之间的变换，可以用矩阵运算来表示。而矩阵运算的数学工具已经相当丰富了。

---

Presburger表示：

\[S=\{(i,j): 0 \le i<R \land 0 \le j<C \}\]

访问函数：从迭代空间到数据空间的一个映射关系。一般可表示为如下矩阵形式：

\[S(i)=Fi+f\]

其中，i为循环迭代向量，S表示数组的下标向量。F和f分别为系数和常数。

所有不破环原有程序语义中的数据依赖的访问遍历顺序都是合法的，这个遍历顺序被称为一种调度。显然不同调度的性能是不同的，循环优化算法的目标就是找到其中的最优调度。

---

依赖分析：读后写依赖，写后写依赖，写后读依赖。

doall循环：没有依赖的循环。

doacross循环：有依赖的循环。

依赖判断的充要条件是：

\[F_1i_1+f_1=F_2i_2+f_2\]

求上述等式整数解的问题是一个典型的整数规划问题。但后者已经确认是个NP完全问题。

所以编译器通常用Banerjee测试和GCD测试来检测依赖。

访问函数非满秩 <=> 存在数据依赖 <=> 映射到同一个处理器

---

几种基础的仿射变换：

• 循环交换（loop permutation）：交换内层循环和外层循环的次序。\(S(i,j)\to (j,i)\)
• 循环反转（loop reversal）：按照相反的顺序执行一个循环中的所有迭代。\(S(i)\to (-i)\)
• 循环倾斜（loop skewing）：对原始循环的迭代空间进行坐标变换。\(S(i,j)\to (i, f\times i+j)\)

上面3种被称为幺模变换。

• 循环延展（loop scaling）：将循环索引变量和循环步长做等比例缩放。\(S(i)\to (s\times i)\)
• 循环合并（loop fusion）：将原程序中的多个循环下标映射到同一个循环下标上。\(S1(i)\to (i, 0);S2(i)\to (i, 1)\)
• 循环分布（loop distribution/fission）：将不同语句的同一个循环下标映射到不同的循环下标。\(S1(i)\to (0,i);S2(i)\to (1,i)\)
• 循环偏移（loop shifting）：将一个动态语句实例偏移固定多个循环迭代。\(S(i)\to (i+c)\)

上面7种被称为基础仿射变换。

• 循环分段（loop strip-mining）：将某维度的迭代拆成两个粒度，比如先以4步长遍历、4步长内以1步长遍历。
• 循环分块（loop tiling）：将对一个大数组的遍历访问拆成更多维度，以利用局部性，比如将调度（i, j）改为 (i/4, j/4, i, j)。它实际等同是循环分段+循环交换。
• 循环展开压紧（loop unroll and jam）：提升外层循环的粒度，并向内压紧。

这几种涉及除法，被称为近似仿射变换。无论基础仿射变换，还是近似仿射变换，都是改变指令实例执行顺序的变换。

除此之外，还有一些不改变指令实例执行顺序的变换：

• 分块分离（loop tile isolation），分块有时会分出半块，导致循环内部有一些判断语句是用于处理这部分计算的。把它们分走，避免冗余判断。
• 循环展开（loop unrolling），降低循环条件本身的判断代价。
• 循环判断外提（loop unswitching），循环剥离（loop peeling）等。
• 循环压紧（loop coalescing/linearization），其实就是线性化；这一般是要被避免的，这种变换使循环的结构丧失了。

参考：

https://zhuanlan.zhihu.com/p/604571955

常见的循环变换

---

weight stationary (WS), output stationary (OS), input stationary (IS), Weight Stationary - Local Output Stationary (WS-LOS), Output Stationary - Local Weight Stationary (OS-LWS).

---

http://www.jos.org.cn/jos/ch/reader/create_pdf.aspx?file_no=5563

基于多面体模型的编译“黑魔法”

https://zhuanlan.zhihu.com/p/310142893

编译器领域的多面体模型

https://zhuanlan.zhihu.com/p/111680367

Polyhedral Model, Interval Analysis and Compilers

https://www.zhihu.com/question/65708935

深入学习auto vectorization和polyhedral变换方面的优化技术有哪些资料？

https://pliss2019.github.io/albert_cohen_slides.pdf

Polyhedral Compilation as a Design Pattern for Compiler Construction

https://mp.weixin.qq.com/s/QEooKxP1sm5O90AUiqKQEQ

Polyhedral Model—AI芯片软硬件优化利器（一）

https://mp.weixin.qq.com/s/NRtud1UImE5ArZ2zQWFRyg

Polyhedral Model—AI芯片软硬件优化利器（二）

https://mp.weixin.qq.com/s/bLBIrJb82IsnyoXSEr2xtw

Polyhedral Model—AI芯片软硬件优化利器（三）

https://www.cnblogs.com/XianghuanHe/articles/15432300.html

编译原理（龙书）第十一章 并行和局部优化学习笔记

https://mp.weixin.qq.com/s/wjk2Mxhd2NDpH72l3rdqgQ

多面体编译技术在软硬协同设计中的应用

https://mp.weixin.qq.com/s/mBheJ9NG8khcLRshI40b2w

AI编译关键技术 • 高层循环编译优化 - 不仅仅是分块和合并

https://zhuanlan.zhihu.com/p/199683290

Polyhedral编译调度算法(1)——Pluto算法

https://zhuanlan.zhihu.com/p/232070003

Polyhedral编译调度算法(2)——Feautrier算法

https://zhuanlan.zhihu.com/p/259311866

Polyhedral编译调度算法(3)——isl中的调度算法

https://zhuanlan.zhihu.com/p/562552075

多面体编译通览

https://zhuanlan.zhihu.com/p/566454197

PLuTo编译器和它的调度算法（一）

https://zhuanlan.zhihu.com/p/566904276

PLuTo编译器和它的调度算法（二）

https://zhuanlan.zhihu.com/p/566909546

PLuTo编译器和它的调度算法（三）