• 策略梯度（续）
  • 策略目标函数（Policy Objective Functions）
  • 策略优化（Policy Optimisation）
  • Monte-Carlo Policy Gradient
  • Softmax Policy
  • Gaussian Policy
  • Policy Gradient Theorem
  • 参考
• Actor-Critic
  • 概述
  • Compatible Function Approximation
  • Reducing Variance Using Baseline

策略梯度（续）

策略目标函数（Policy Objective Functions）

首先，我们看看如何评价一个策略的好坏。

• Start value：

\[J_1(\theta)=V^{\pi_\theta}(s_1)=E_{\pi_\theta}[v_1]\]

上式表示在能够产生完整Episode的环境下，从状态\(s_1\)开始，直到结束状态所能获得的累计奖励。在这种情况下，由于整个Episode的状态、路径都是确定的，因此奖励也是确定的。我们需要做的只是最大化start value，以找到最佳路径（也就是最佳策略）。

• Average Value：

\[J_{avV}(\theta)=\sum_s d^{\pi_\theta}(s)V^{\pi_\theta}(s)\]

对于连续环境条件，不存在一个开始状态，这个时候可以使用average value。上式中的\(d^{\pi_\theta}(s)\)表示\(\pi_\theta\)对应的MDP过程的Markov chain的稳态分布。

• Average reward per time-step：

\[J_{avR}(\theta)=\sum_s d^{\pi_\theta}(s)\sum_a\pi_\theta(s,a)R_{s,a}\]

上式表示每一个time-step在各种情况下所能得到的平均奖励。

当然了，在很多情况下，我们未必可以得到一个真实的奖励值，这时使用相关函数的估计值作为奖励值即可。

策略优化（Policy Optimisation）

主要分为两大类：

1.非gradient算法。

• Hill climbing
• Simplex / amoeba / Nelder Mead
• Genetic algorithms

2.gradient算法。

• Gradient descent
• Conjugate gradient
• Quasi-newton

一般来说，gradient算法的优化效率较高，因此本文只讨论gradient算法。

我们可以仿照ML中的梯度优化算法，定义策略的梯度函数：

\[\Delta\theta=\alpha\nabla_\theta J(\theta)\]

其中，

\[\nabla_\theta J(\theta)=\begin{bmatrix} \frac{\partial J(\theta)}{\partial \theta_1} \\ \vdots \\ \frac{\partial J(\theta)}{\partial \theta_n} \end{bmatrix}\]

然而，梯度函数有的时候并不简单，也许并不可微。这时可以使用有限差分法：

\[\frac{\partial J(\theta)}{\partial \theta_k}\approx \frac{J(\theta + \epsilon u_k)-J(\theta)}{\epsilon}\]

这里的\(u_k\)是第k个元素为1，其余元素为0的单位向量。

有限差分法简单，不要求策略函数可微分，适用于任意策略；但有噪声，且大多数时候不高效。

Monte-Carlo Policy Gradient

\[\nabla_\theta \pi_\theta(s,a) = \pi_\theta(s,a)\frac{\nabla_\theta \pi_\theta(s,a)}{\pi_\theta(s,a)}=\pi_\theta(s,a) \nabla_\theta \log \pi_\theta(s,a)\]

上式一般被称作Likelihood ratios，这里使用到了一个公式：\(\mathrm{d}\log(y)=\mathrm{d}y/y\)

我们定义Score function为：\(\nabla_\theta \log \pi_\theta(s,a)\)

下面讨论几种常见的策略。

Softmax Policy

Softmax Policy适用于离散行为空间，它把行为权重看成是多个特征在一定权重下的线性代数和：\(\phi(s,a)^T\theta\)，则采取某一行为的概率为：

\[\pi_\theta(s,a)\propto e^{\phi(s,a)^T\theta}\]

相应的Score function为:

\[\nabla_\theta \log \pi_\theta(s,a)=\phi(s,a)-E_{\pi_\theta}[\phi(s,\cdot)]\]

上式中，等号右边第一部分是采取某行为的Score，第二部分是当前状态的期望分值。

Gaussian Policy

Gaussian Policy适用于连续行为空间。比如，如果控制机器人行走要调整流经某个电机的电流值，而这个电流值是连续值。

它用一个正态分布表示策略：\(a\sim N(\mu(s), \sigma^2)\)，其中\(\mu(s)=\phi(s)^T\theta\)。

相应的Score function为:

\[\nabla_\theta \log \pi_\theta(s,a)=\frac{(a-\mu(s))\phi(s)}{\sigma^2}\]

下面我们用一个图来演示一下相关步骤。

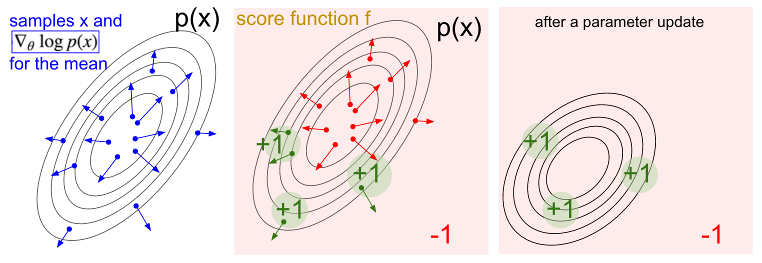
左图的蓝点表示采样X，箭头指示该点的梯度方向，既然是正态分布，这些箭头显然是远离中心的。中图表示，X对应的Score function。我们根据Score function更新参数（沿着绿色箭头方向，或者沿着红色箭头的反方向）。最终得到右图中的新的正态分布。

从贝叶斯学习的角度来看，左图相当于先验分布，而中图相当于后验分布。

参考：

https://karpathy.github.io/2016/05/31/rl/

Deep Reinforcement Learning: Pong from Pixels

Policy Gradient Theorem

One-Step MDP是一类特殊的MDP：它从任意状态开始，只执行一次动作，然后就结束了。

\[J(\theta)=E_{\pi_\theta}[r]=\sum_{s\in S} d(s)\sum_{a\in A}\pi_\theta(s,a)R_{s,a}\] \[\nabla_\theta J(\theta)=\sum_{s\in S} d(s)\sum_{a\in A}\nabla_\theta \log \pi_\theta(s,a)R_{s,a}=E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a)r]\]

One-Step MDP的相关结论可以扩展到multi-step MDP，只需要将即时奖励r，替换为长期奖励（一般使用其估计函数\(Q^{\pi}(s,a)\)）即可。

在监督学习里，当前状态、行为的好坏由监督信息告知；而在强化学习里，则需要通过价值函数来估计当前状态行为的好坏。

我们将Policy Gradient应用到MC算法上，则得到如下流程：

Initialise \(\theta\) arbitrarily

for each episode \(\{s_1,a_1,r_2,\dots,s_{T−1},a_{T−1},r_T\}\sim \pi_\theta\) {

for t = 1 to \(T−1\) {
\(\theta \leftarrow \theta + \alpha\nabla_\theta \log \pi_\theta (s_t , a_t )v_t\)
}

}

return \(\theta\)

在基于策略的学习算法中，算法挑选策略的时候不需使用\(\epsilon\)-贪婪搜索，策略是直接根据参数\(\theta\)得到的。同时在对策略参数更新时有一个学习率\(\alpha\)，它体现了在梯度方向上更新参数θ的步长（step size），一般的我们在更新参数时是按梯度方向只更新由\(\alpha\)确定的一定量。

打个比方，当前策略在更新时提示梯度方向倾向于选择“向左”的行为，那么在更新策略参数时，可以朝着向左的方向更新一定的值，如果这个\(\alpha\)取值增大，则导致决策朝着更容易选择“向左”的行为倾斜，这其实就相当于没有探索的贪婪决策行为。而只要学习在持续，就有可能因为梯度变化而尝试更多的行为，这一过程中参数\(\alpha\)控制了策略更新的平滑度。

如果基于价值函数制定策略，则使用查表（table look-up)的方式可以保证收敛到全局最优解。即使使用的是直接基于策略的学习方法；但是,如果使用的是通用化的近似函数表示方法，比如神经网络等，则无论是基于价值函数，还是基于策略，都可能陷入局部最优解。

参考

https://zhuanlan.zhihu.com/p/54825295

基于值和策略的强化学习入坑

https://blog.csdn.net/gsww404/article/details/80705950

策略梯度（Policy Gradient）

https://zhuanlan.zhihu.com/p/122663529

从Mirror Descent的视角统一强化学习中的策略优化

https://mp.weixin.qq.com/s/a7KN3IjuMcmHNNqQsPn3VQ

函数近似的策略梯度方法

Actor-Critic

概述

MC策略梯度方法使用了收获作为状态价值的估计，它虽然是无偏的，但是噪声却比较大，也就是变异性（方差）较高。如果我们能够相对准确地估计状态价值，用它来指导策略更新，那么是不是会有更好的学习效果呢？这就是Actor-Critic策略梯度的主要思想。

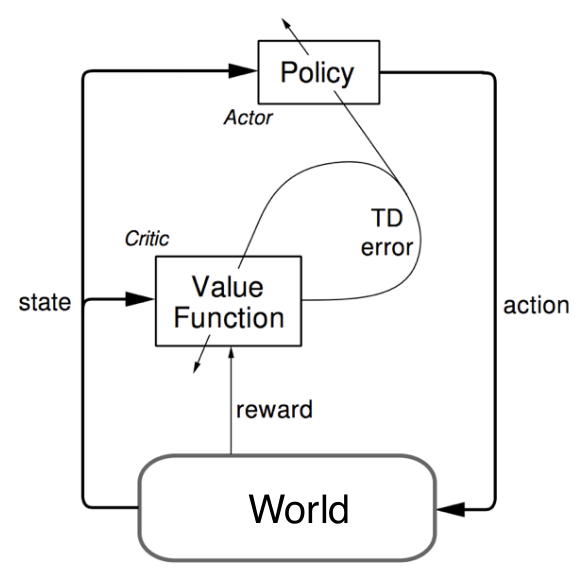
Actor-Critic的字面意思是“演员-评论”，相当于演员在演戏的同时，有评论家指点，继而演员演得越来越好。即使用Critic来估计行为价值：

\[Q_w(s,a)\approx Q^{\pi_\theta}(s,a)\]

基于Actor-Critic策略梯度学习分为两部分内容：

1.Critic：更新action-value函数的参数w。

2.Actor：按照Critic得到的价值，引导策略函数参数\(\theta\)的更新。

\[\nabla_\theta J(\theta)\approx E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a)Q_w(s,a)]\] \[\Delta \theta = \alpha \nabla_\theta \log \pi_\theta(s,a)Q_w(s,a)\]

可以看出，Critic做的事情其实是我们已经见过的：策略评估，他要告诉个体，在由参数\(\theta\)确定的策略\(\pi_\theta\)到底表现得怎么样。

Compatible Function Approximation

近似策略梯度的方法引入了Bias，从而得到的策略梯度不一定能最后找到较好的解决方案，例如当近似价值函数引起状态重名的特征时。

幸运的是，如果我们小心设计近似函数，是可以避免引入bias的。该近似函数需要满足下面两个条件:

• 近似价值函数的梯度完全等同于策略函数对数的梯度，即不存在重名情况：

\[\nabla_w Q_w(s,a)=\nabla_\theta \log \pi_\theta(s,a)\]

• 价值函数参数w使得均方差最小：

\[\epsilon = E_{\pi_\theta}[(Q^{\pi_\theta}(s,a)-Q_w(s,a))^2]\]

符合这两个条件，则认为策略梯度是准确的，即：

\[\nabla_\theta J(\theta)= E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a)Q_w(s,a)]\]

Reducing Variance Using Baseline

除了bias之外，variance也是需要考虑的方面。

我们从策略梯度里抽出一个基准函数B(s)，要求这一函数仅与状态有关，而与行为无关，因而不改变梯度本身。

\[E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a)B(s)] = \sum_{s\in S} d^{\pi_\theta}(s)\sum_{a\in A}\nabla_\theta \pi_\theta(s,a)B(s)\\= \sum_{s\in S} d^{\pi_\theta}(s)B(s) \nabla_\theta \sum_{a\in A} \pi_\theta(s,a) = 0\]

由于B(s)与行为无关，可以将其从针对行为a的求和中提出来，同时我们也可以把梯度从求和符号中提出来，而最后一个求和项：策略函数针对所有行为的求和，根据策略函数的定义，这里的结果肯定是1。而常数的梯度是0，因此总的结果等于0。

原则上，和行为无关的函数都可以作为B(s)。一个很好的B(s)就是基于当前状态的状态价值函数：\(V^{\pi_\theta}(s)\)。

所以，我们可以用一个advantage function来改写策略梯度：

\[A^{\pi_\theta}(s,a)=Q^{\pi_\theta}(s,a)-V^{\pi_\theta}(s)\]

上式的现实意义在于评估当个体采取行为a离开s状态时，究竟比该状态s总体平均价值要好多少？

\[\nabla_\theta J(\theta)= E_{\pi_\theta}[\nabla_\theta \log \pi_\theta(s,a)A^{\pi_\theta}(s,a)]\]

advantage function可以明显减少状态价值的variance。（通俗的说法就是A的值有正有负，不像Q和V都是正值。）

因此，现在Critic的任务就改为估计advantage function。

在这种情况下，我们需要两个近似函数也就是两套参数，一套用来近似状态价值函数，一套用来近似行为价值函数。即：

\[V_v(s)\approx V^{\pi_\theta}(s)\] \[Q_w(s,a)\approx Q^{\pi_\theta}(s,a)\] \[A(s,a) = Q_w(s,a) - V_v(s)\]

不过实际操作时，我们并不需要计算两个近似函数。这里以TD学习为例说明一下。