• Model-Free Control（续）
  • Importance Sampling for Off-Policy TD
  • DP和TD的关系
• 价值函数的近似表示（Value Function Approximation）
  • 线性函数
  • Incremental Prediction Algorithms
  • Batch Methods
    • Least Squares Prediction
    • Experience Replay
• 策略梯度（Policy Gradient）
  • 随机策略

Model-Free Control（续）

Importance Sampling for Off-Policy TD

类似的，TD算法的更新公式为：

\[V(S_t)\leftarrow V(S_t)+\alpha\left(\frac{\pi(A_t\mid S_t)}{\mu(A_t\mid S_t)}(R_{t+1}+\gamma V(S_{t+1}))-V(S_t)\right)\]

应用这种思想最好的方法是基于TD(0)的Q-learning。Q-learning的相关内容参见《强化学习（二）》。

DP和TD的关系

	Full Backup (DP)	Sample Backup (TD)
Bellman Expectation Equation for \(v_\pi(s)\)	Iterative Policy Evaluation \(V(s)\leftarrow E[R+\gamma V(S')\mid s]\)	TD Learning \(V(S)\xleftarrow{\alpha} R+\gamma V(S')\)
Bellman Expectation Equation for \(q_\pi(s,a)\)	Q-Policy Iteration \(Q(s,a)\leftarrow E[R+\gamma Q(S',A')\mid s,a]\)	Sarsa \(Q(S,A)\xleftarrow{\alpha} R+\gamma Q(S',A')\)
Bellman Optimality Equation for \(q_*(s,a)\)	Q-Value Iteration \(Q(s,a)\leftarrow E[R+\gamma \max_{a'\in A}Q(S',a')\mid s]\)	Q-Learning \(Q(S,A)\xleftarrow{\alpha} R+\gamma \max_{a'\in A}Q(S',a')\)

上表中\(x\xleftarrow{\alpha}y\equiv x\leftarrow x+\alpha(y-x)\)。

价值函数的近似表示（Value Function Approximation）

之前的内容都是讲解一些强化学习的基础理论，这些知识只能解决一些中小规模的问题。很多价值函数需要用一张大表来存储。当获取某一状态或行为的价值的时候，通常需要一个查表操作（Table Lookup），这对于那些状态空间或行为空间很大的问题几乎无法求解。

在实际应用中，对于状态和行为空间都比较大的情况，精确获得各种v(s)和q(s,a)几乎是不可能的。这时候需要找到近似的函数。具体来说，可以使用线性组合、神经网络以及其他方法来近似价值函数：

\[\begin{array}\\ \hat v(s,w)\approx v_\pi(s)\\ \hat q(s,a,w)\approx q_\pi(s,a) \end{array}\]

其中w是该近似函数的参数。

线性函数

这里仍然从最简单的线性函数说起：

\[\hat v(S,w)=x(S)^Tw=\sum_{j=1}^nx_j(S)w_j\]

目标函数为：

\[J(w)=E_\pi[(v_\pi(S)-x(S)^Tw)^2]\]

更新公式为：

\[\Delta w=\alpha (v_\pi(S)-\hat v(S,w))x(S)\]

上述公式都是基本的ML方法，这里不再赘述。

最简单的一类线性函数，被叫做Table Lookup Features：

\[x^{table}(S)=\begin{bmatrix} 1(S=s_1) \\ \vdots \\ 1(S=s_n) \end{bmatrix}\]

则：

\[\hat v(S,w)=\begin{bmatrix} 1(S=s_1) \\ \vdots \\ 1(S=s_n) \end{bmatrix}\begin{bmatrix} w_1 \\ \vdots \\ w_n \end{bmatrix}\]

Incremental Prediction Algorithms

事实上，之前所列的公式都不能直接用于强化学习，因为公式里都有一个实际价值函数\(v_\pi(S)\)，或者是一个具体的数值，而强化学习没有监督数据，因此不能直接使用上述公式。

因此，我们需要找到一个替代\(v_\pi(S)\)的目标函数。

MC	\(\Delta w=\alpha ({\color{red}{G_t}}-\hat v(S_t,w))\nabla_w \hat v(S_t,w)\)	有噪声、无偏采样	收敛至一个局部最优解
TD(0)	\(\Delta w=\alpha ({\color{red}{R_{t+1}+\gamma\hat v(S_{t+1},w)}}-\hat v(S_t,w))\nabla_w \hat v(S_t,w)\)	有噪声、有偏采样	收敛至全局最优解
TD(\(\lambda\))	\(\Delta w=\alpha ({\color{red}{G_t^\lambda}}-\hat v(S_t,w))\nabla_w \hat v(S_t,w)\)	有噪声、有偏采样

上面公式中，红色的部分就是目标函数。

对于\(\hat q(S,A,w)\)，我们也有类似的结论：

MC	\(\Delta w=\alpha ({\color{red}{G_t}}-\hat q(S_t,A_t,w))\nabla_w \hat q(S_t,A_t,w)\)	有噪声、无偏采样	收敛至一个局部最优解
TD(0)	\(\Delta w=\alpha ({\color{red}{R_{t+1}+\gamma\hat q(S_{t+1},A_{t+1},w)}}-\hat q(S_t,A_t,w))\nabla_w \hat q(S_t,A_t,w)\)	有噪声、有偏采样	收敛至全局最优解
TD(\(\lambda\))	\(\Delta w=\alpha ({\color{red}{q_t^\lambda}}-\hat q(S_t,A_t,w))\nabla_w \hat q(S_t,A_t,w)\)	有噪声、有偏采样

下面给出各种算法的收敛特性。

预测算法的收敛性：

On/Off-Policy	Algorithm	Table Lookup	Linear	Non-Linear
On-Policy	MC TD(0) TD(\(\lambda\)) Gradient TD	Yes Yes Yes Yes	Yes Yes Yes Yes	Yes No No Yes
On-Policy	MC TD(0) TD(\(\lambda\)) Gradient TD	Yes Yes Yes Yes	Yes No No Yes	Yes No No Yes

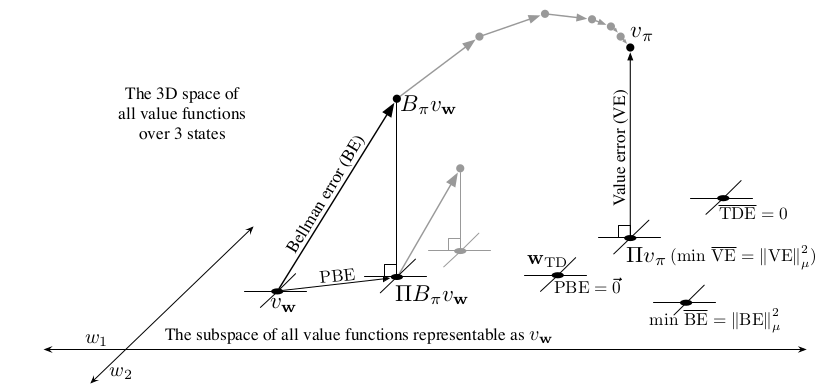
Gradient TD中的Gradient指的是PBE（projected Bellman error）的梯度。

控制算法的收敛性：

Algorithm	Table Lookup	Linear	Non-Linear
Monte-Carlo Control Sarsa Q-learning Gradient Q-learning	Yes Yes Yes Yes	Yes’ Yes’ No Yes	No No No No

Yes’ = chatters around near-optimal value function

Batch Methods

前面所说的Incremental算法都是基于数据流的，经历一步，更新算法后，我们就不再使用这步的数据了，这种算法简单，但有时候不够高效。与之相反，Batch Methods则是把一段时期内的数据集中起来，通过学习来使得参数能较好地符合这段时期内所有的数据。这里的训练数据集Batch相当于个体的一段经验。

Least Squares Prediction

假设存在一个价值函数的近似：\(\hat v(s,w)\approx v_\pi(s)\)和一个经验集\(\mathcal{D}=\{<s_1,v_1^{\pi}>,<s_2,v_2^{\pi}>,\dots,<s_T,v_T^{\pi}>\}\)，则Least Squares Error为：

\[LS(w)=\sum_{t=1}^T(v_t^{\pi}-\hat v(s_t,w))^2\]

使用LSE的Prediction被称为Least Squares Prediction，针对不同方向衍生还出了LSMC、LSTD、LSTD(\(\lambda\))等算法。

LSE亦可推广到Q函数，即所谓的LS Q-Learning。

Experience Replay

为了充分利用经验集，我们还可以使用Experience Replay技术，即：随机从\(\mathcal{D}\)中采样\(<s,v^{\pi}>\)，然后使用SGD最小化LSE。

这一点和普通的监督学习很类似，梯度下降从原理上来说，本就不可能一个epoch就达到最优，而需要多跑几个epoch，这里的Experience Replay也是类似的道理。

Experience Replay还可用来消除训练数据间的相关性。例如，1个agent在1个episode中产生的experience就是相关的，\(<s_t,a_t>\)和\(<s_{t+1},a_{t+1}>\)显然存在着一定的逻辑关系。训练数据间的相关性会影响算法收敛到最优解。

策略梯度（Policy Gradient）

价值函数可以进行近似的参数化表达，策略本身也同样可以函数化、参数化：

\[\pi_\theta(s,a)=P[a | s, \theta]\]

所谓函数化是指，通过一个概率分布函数\(\pi_\theta(s,a)\)，来表示每一步的最优策略，在每一步根据该概率分布进行action采样，获得当前的最佳action取值。显然概率越高的a，就是该策略最倾向的a。

显然，生成action的过程，本质上是一个随机过程；最后学习到的策略，也是一个随机策略(stochastic policy).

而策略函数的参数化就和价值函数的参数化类似了，无非是用较少的参数，来表示巨大的状态空间而已。

基于策略学习的优点：

• 基于策略的学习可能会具有更好的收敛性，这是因为基于策略的学习虽然每次只改善一点点，但总是朝着好的方向在改善；但是上讲提到有些价值函数在后期会一直围绕最优价值函数持续小的震荡而不收敛。

• 在对于那些拥有高维度或连续状态空间来说，使用基于价值函数的学习在得到价值函数后，制定策略时，需要比较各种行为对应的价值大小，这样如果行为空间维度较高或者是连续的，则从中比较得出一个有最大价值函数的行为这个过程就比较难了，这时候使用基于策略的学习就高效的多。

连续行为空间内的action对应一个具体的数值，这个数值可以从上述的策略分布中随机采样产生。因此策略学习天生支持连续行为空间。

• 能够学到一些随机策略。这一点后文会详述。

• 有时候计算价值函数非常复杂。比如当小球从从空中某个位置落下你需要左右移动接住时，计算小球在某一个位置时采取什么行为的价值是很难得；但是基于策略就简单许多，你只需要朝着小球落地的方向移动修改策略就行。

缺点：

• 容易收敛到局部最优，而非全局最优。

• 因为基于价值函数的策略决定每次都是推促个体去选择一个最大价值的行为；但是基于策略的，更多的时候策略的选择时仅会在策略某一参数梯度上移动一点点，使得整个的学习比较平滑，因此不够高效。

随机策略

随机策略有时是最优策略。对于石头剪刀布的游戏，只要一方有一个确定性的策略，就会被对手抓住进而整体上输掉。这个时候最好的策略就是随机选择每次出法，以得到最大可能的总体奖励。

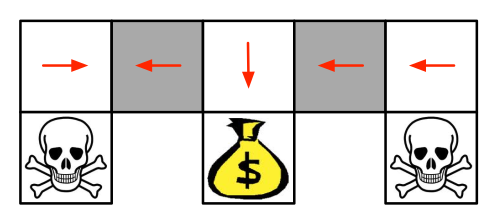
以上面的Gridworld图为例，如果我们用某一个格子的某个方向是否有墙挡住来描述格子状态的话，就会发生灰色格子的状态是一样的情况，这就是所谓的状态重名（Aliased）。

在这种情况下，如果采用确定性的策略话，在个体处于无论哪个灰色格子时，都只能选取相同的行为。假设个体现在学到了一个价值函数，在这个价值函数里状态就是基于上述特征的参数化表示，此时当个体处在灰色格子中，如果采取的是greedy执行的方式，价值函数给出的策略要么都是向东，要么都是向西。如果是向西，那么当个体处在左侧灰色格子时，它将一直（greedy）或很长时间（\(\epsilon\)-greedy）徘徊在长廊左侧两个格子之间而无法到达有钱袋子的格子，因而很长时间得不到奖励。

当发生状态重名情况时，随机策略将会优于确定性的策略。之前的理论告诉我们，对于任何MDP总有一个确定性的最优策略。不过那是针对状态可完美观测、或者使用的特征可以完美描述状态的情况下的。当发生状态重名无法区分，或者使用的近似函数无法对状态完美描述时，个体得到的状态信息等效于部分观测的环境信息，这时问题将不具备Markov性。而此时的最优策略，也不再是确定性的。