• Temporal-Difference Learning
  • 反向认识TD(\(\lambda\))（续）
• Model-Free Control
  • 概述
  • On-Policy Monte-Carlo Control
  • On-Policy Temporal-Difference Learning
  • 采样方法
    • Inverse Sampling
    • Rejective Sampling
    • Importance Sampling
  • Off-Policy Learning
    • Importance Sampling for Off-Policy Monte-Carlo

Temporal-Difference Learning

反向认识TD(\(\lambda\))（续）

结合之前提到的TD error和ET，则更新公式可改为：

\[V(S_t)\leftarrow V(S_t)+\alpha\delta_tE_t(s)\]

如果\(\lambda=0\)，则只有当前状态得到更新，即\(E_t(s)=1(S_t=s)\)，这实际上就和之前提到TD(n=0)算法是一致的了。

David Silver的课件在这里存在表示混乱的问题，在之前的章节中，TD(X)表示的是n=X，而下文中TD(X)有的时候指的是\(\lambda=X\)。这里借用python表示参数的语法，更准确的描述公式。

如果\(\lambda=1\)，TD(\(\lambda=1\))粗略看与每次访问的MC算法等同；在线更新时，状态价值差每一步都会有积累；离线更新时，TD(\(\lambda=1\))等同于MC算法(即遍历整个Episode)。

参考：

https://mp.weixin.qq.com/s/X6bukOqZ2Eg7jZ6MydHwSg

伯克利提出时序差分模型TDM：让深度强化学习更像人类

Model-Free Control

概述

之前提到的MC & TD都是Model-free prediction，下面讲讲Model-Free Control。

现实中有很多此类的例子，比如控制一个大厦内的多个电梯使得效率最高；控制直升机的特技飞行，机器人足球世界杯上控制机器人球员，围棋游戏等等。所有的这些问题要么我们对其模型运行机制未知，但是我们可以去经历、去试；要么是虽然问题模型是已知的，但问题的规模太大以至于计算机无法高效的计算，除非使用采样的办法。Model-Free Control的内容就专注于解决这些问题。

我们之前已经指出了MDP的五要素：

\[<\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma>\]

从形式定义的角度来说，Model-Free Control实际上就是一种\(\mathcal{P},\mathcal{R},\gamma\)均为未知的MDP。

根据优化控制过程中是否利用已有或他人的经验策略来改进我们自身的控制策略，我们可以将这种优化控制分为两类：

一类是On-policy Learning，其基本思想是个体已有一个策略，并且遵循这个策略进行采样，或者说采取一系列该策略下产生的行为，根据这一系列行为得到的奖励，更新状态函数，最后根据该更新的价值函数来优化策略得到较优的策略。

另一类是Off-policy Learning: 其基本思想是，虽然个体有一个自己的策略，但是个体并不针对这个策略进行采样，而是基于另一个策略进行采样，这另一个策略可以是先前学习到的策略，也可以是人类的策略等一些较为优化成熟的策略，通过观察基于这类策略的行为，或者说通过对这类策略进行采样，得到这类策略下的各种行为，继而得到一些奖励，然后更新价值函数，即在自己的策略形成的价值函数的基础上观察别的策略产生的行为，以此达到学习的目的。这种学习方式类似于“站在别人的肩膀上可以看得更远”。

简单来说，On-policy Learning训练时，使用当前策略，而Off-policy Learning使用非当前策略。

参考：

https://zhuanlan.zhihu.com/p/346433931

On-policy与off-policy

On-Policy Monte-Carlo Control

Model-Free Control应用MC需要解决两个问题：

1.在模型未知的条件下无法知道当前状态的所有后续状态，进而无法确定在当前状态下采取怎样的行为更合适。

解决这一问题的方法是使用action-value function：\(q_{\pi}(s; a)\)替换state-value function：\(v_{\pi}(s)\)。即下图所示：

这样做的目的是可以改善策略而不用知道整个模型，只需要知道在某个状态下采取什么样的行为价值最大即可。

2.当我们每次都使用贪婪算法来改善策略的时候，将很有可能由于没有足够的采样经验而导致产生一个并不是最优的策略，我们需要不时的尝试一些新的行为，这就是探索（Exploration）。

一般使用《强化学习（二）》中提到的\(\epsilon\)-greedy算法，解决这个问题，这里不再赘述。

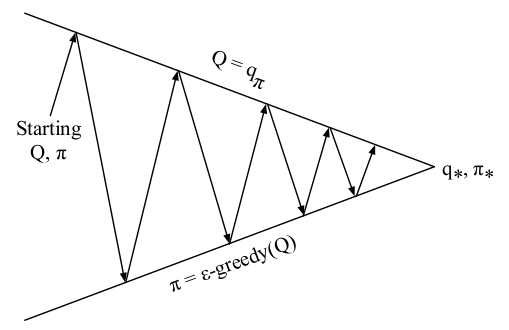
这个图建议和《强化学习（三）》中Policy Iteration一节的类似图，对比着看。可以看出无论是Q函数迭代还是V函数迭代，都会收敛到最佳策略\(\pi\)。

上图中每一个向上或向下的箭头都对应着多个Episode。也就是说我们一般在经历了多个Episode之后才进行一次Ｑ函数更新或策略改善。实际上我们也可以在每经历一个Episode之后就更新Ｑ函数或改善策略。但不管使用那种方式，在Ɛ-贪婪探索算法下，我们始终只能得到基于某一策略下的近似Ｑ函数，且该算法没有一个终止条件，因为它一直在进行探索。

因此我们必须关注以下两个方面：一方面我们不想丢掉任何更好信息和状态，另一方面随着我们策略的改善我们最终希望能终止于某一个最优策略，因为事实上最优策略不应该包括一些随机行为选择。为此引入了另一个理论概念：GLIE。

GLIE(Greedy in the Limit with Infinite Exploration)，直白的说就是在无限可能的探索中，逐渐逼近极限。具体表现为：所有已经经历的状态行为对（state-action pair）会被无限次探索；另外随着探索的无限延伸，贪婪算法中\(\epsilon\)值趋向于0。例如，如果我们取\(\epsilon=1/k\)（k为探索的Episode数目），那么该\(\epsilon\)-greedy MC Control就具备GLIE特性。

基于GLIE的MC Control流程如下：

1.对于给定策略\(\pi\)，采样第k个Episode：\(\{S_1,A_1,R_2,\dots,S_T\}\sim \pi\)

2.对于该Episode里出现的每一个状态/行为对更新：

\[\begin{array}\\ N(S_t,A_t)\leftarrow N(S_t,A_t)+1\\ Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\frac{1}{N(S_t,A_t)}(G_t-Q(S_t,A_t)) \end{array}\]

3.基于新的Q函数改善：

\[\epsilon\leftarrow 1/k,\pi\leftarrow \epsilon-greedy(Q)\]

On-Policy Temporal-Difference Learning

TD在On-Policy的应用主要是Sarsa算法。Sarsa是State–action–reward–state–action的缩写。

Sarsa算法的流程如下所示：

随机初始化\(Q(s,a)\)，其中\(Q(\text{terminal-state},\cdot)=0\)。
每个Episode执行：

初始化S
根据Q选择当前S下的A
对Episode中的每一步执行：

执行A，获得观察值R,S’
根据Q选择当前S’下的A’
\(Q(S,A)\leftarrow Q(S,A)+\alpha [R+\gamma Q(S',A')-Q(S,A)]\)
\(S\leftarrow S',A\leftarrow A'\)

直到S是terminal状态。

Sarsa算法的最优化收敛性（即\(Q(s,a)\to q_*(s,a)\)）的条件是：

1.策略产生的序列满足GLIE。

2.\(\alpha_t\)满足Robbins–Monro特性，即：

\[\sum_{t=1}^\infty \alpha_t=\infty, \sum_{t=1}^\infty \alpha_t^2<\infty\]

Herbert Ellis Robbins，1915～2001，美国数学家，Harvard博士，University of North Carolina教授，Columbia University教授。美国艺术科学院、美国科学院院士。

Sutton Monro，1920～1995，美国数学家，MIT博士，Lehigh University教授。作为海军参加过二战和韩战。

和TD类似，我们也可以定义n-step的Sarsa(n)算法

\[Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha(q_t^{n}-Q(S_t,A_t))\]

Sarsa(\(\lambda\))：

\[Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha(q_t^{\lambda}-Q(S_t,A_t))\]

Sarsa(\(\lambda\))+ET：

\[Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha\delta_tE_t(s,a)\]

参考：

https://blog.csdn.net/zchang81/article/details/77746313

Sarsa与Q-learning对比

采样方法

在继续后面的内容之前，我们首先介绍几种采样方法。

Inverse Sampling

如果某种分布函数不容易采样的话，可以使用它的反函数进行采样：

\[P(F^{-1}(a) \le x) = P(a \le F(x)) = H(F(x))\]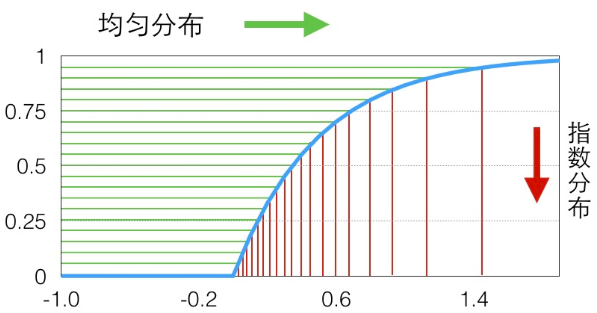

上图是均匀分布到指数分布的采样图，其中y的采样间隔是：

\[F^{-1}_{exp}(a) = -\frac{1}{\lambda}*log(1-a)\]

参考：

https://mp.weixin.qq.com/s/1xGbbY0iJ-oBn3Uw0CwYag

用逆变换采样方法构建随机变量生成器

Rejective Sampling

我们想求一个空间里均匀分布的集合面积，可以尝试在更大范围内按照均匀分布随机采样，如果采样点在集合中，则接受，否则拒绝。

这种方法最经典的例子就是采样计算圆周率：我们在一个1x1的范围内随机采样一个点，如果它到原点的距离小于1,则说明它在1/4圆内，则接受它，最后通过接受的占比来计算1/4圆形的面积，从而根据公式反算出预估的\(\pi\)值，随着采样点的增多，最后的结果会越精准。

Rejective Sampling的形式化表述为：

\[acc(x_i) = \frac{\tilde{p}(x_i)}{cq(x_i)}\]

其中，\(\tilde{p}(x_i)\)是实际采样的样本，它应该正比于目标分布，\(cq(x_i)\)是比例系数，c为常数。在上例中，\(q(x_i)\)是均匀分布，所以就是常数1，如果是其它分布的话，则是一个函数。

Importance Sampling

然而实际工作中，分布的正函数已经很复杂，更不用说反函数，\(cq(x_i)\)也不是那么容易得到的，这时就需要Importance Sampling了。

我们采样的目标是：

\[E_{x\sim p}[f(x)] = \int_x f(x)p(x) \mathrm{d}x\]

如果符合p(x)分布的样本不太好生成，我们可以引入另一个分布q(x)，可以很方便地生成样本。使得：

\[\begin{align} \int_x f(x)p(x) \mathrm{d}x &= \int_x f(x)\frac{p(x)}{q(x)}q(x) \mathrm{d}x\\ &= \int_x g(x)q(x) \mathrm{d}x = E_{x\sim q}[g(x)]\\ where\ \ g(x) &= f(x)\frac{p(x)}{q(x)} = f(x)w(x) \end{align}\]

我们将问题转化为了求g(x)在q(x)分布下的期望。我们称其中的\(w(x)=\frac{p(x)}{q(x)}\)为Importance Weight。

Importance Sampling还可以改善已有的采样方法：如果我们找到一个q分布，使得它能在f(x)∗p(x)较大的地方采集到样本，则能更好地逼近E[f(x)]。

参考：

http://blog.csdn.net/Dark_Scope/article/details/70992266

采样方法

https://mp.weixin.qq.com/s/ZyH_9EBXYaDJxSvVgUaNew

蒙特卡洛积分与重要性采样

Off-Policy Learning

Importance Sampling for Off-Policy Monte-Carlo

前面已经说过，Off-Policy Learning就是根据当前策略\(\mu(a\mid s)\)，评估目标策略\(\pi(a\mid s)\)。因此，对Off-Policy Learning进行Importance Sampling，实际上就是从\(\mu\)中，对\(\pi\)采样的过程。由于MC需要对整个Episode进行采样，因此相应的采样函数为：

\[G_t^{\pi/\mu}=\frac{\pi(A_t\mid S_t)}{\mu(A_t\mid S_t)}\frac{\pi(A_{t+1}\mid S_{t+1})}{\mu(A_{t+1}\mid S_{t+1})}\dots\frac{\pi(A_T\mid S_T)}{\mu(A_T\mid S_T)}G_t\]

更新公式为：

\[V(S_t)\leftarrow V(S_t)+\alpha(G_t^{\pi/\mu}-V(S_t))\]

由于这种方法的采样函数实在太过复杂，因此只有理论价值，而无实际意义。