• Temporal-Difference Learning（续）
  • TD vs. MC—1
  • TD vs. MC—2
  • TD vs. MC—3
  • DP & MC & TD
  • bootstrapping
  • TD(n)
  • Large Random Walk
  • TD(\(\lambda\))
    • 前向认识TD(\(\lambda\))
    • 反向认识TD(\(\lambda\))

Temporal-Difference Learning（续）

TD vs. MC—1

通过这个例子，我们可以直观的了解到：

1.TD在知道结果之前可以学习，MC必须等到最后结果才能学习；

2.TD可以在没有结果时学习，可以在持续进行的环境里学习。

TD vs. MC—2

\(G_t = R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{T−1}R_T\)是\(V_{\pi}(S_t)\)的无偏估计值。

True TD target：\(R_{t+1}+\gamma V_{\pi}(S_{t+1})\)，也是\(V_{\pi}(S_t)\)的无偏估计值。

TD target：\(R_{t+1}+\gamma V(S_{t+1})\)，是\(V_{\pi}(S_t)\)的有偏估计值。

MC没有bias，但有着较高的Variance，且对初始值不敏感；

TD低variance, 但有一定程度的bias，对初始值较敏感，通常比MC更高效；

TD vs. MC—3

再来看如下示例：

现有两个状态(A和B)，MDP未知，衰减系数为1，有如下表所示8个完整Episode的经验及对应的即时奖励，其中除了第1个Episode有状态转移外，其余7个均只有一个状态。

Episode	状态转移及奖励
1	A:0,B:0
2	B:1
3	B:1
4	B:1
5	B:1
6	B:1
7	B:1
8	B:0

问题：依据仅有的Episode，计算状态A，B的价值分别是多少，即V(A)=？， V(B)=？

答案：V(B) = 6/8，V(A)根据不同算法结果不同，用MC算法结果为0，TD则得出6/8。

解释：应用MC算法，由于需要完整的Episode,因此仅Episode1可以用来计算A的状态价值，很明显是0；同时B的价值是6/8。应用TD算法时，TD算法试图利用现有的Episode经验构建一个MDP（图见下节），由于存在一个Episode使得状态A有后继状态B，因此状态A的价值是通过状态B的价值来计算的，同时经验表明A到B的转移概率是100%，且A状态的即时奖励是0，并且没有衰减，因此A的状态价值等于B的状态价值。

MC算法试图收敛至一个能够最小化状态价值与实际收获的均方差的解决方案。TD算法则收敛至一个根据已有经验构建的最大可能的Markov模型的状态价值。

通过比较可以看出，TD算法使用了MDP问题的Markov属性，在Markov环境下更有效；而MC算法并不利用Markov属性，通常在非Markov环境下更有效。

DP & MC & TD

Monte-Carlo, Temporal-Difference和Dynamic Programming都是计算状态价值的一种方法，区别在于：

• 前两种是在不知道Model的情况下的常用方法，这其中MC方法需要一个完整的Episode来更新状态价值，而TD则不需要完整的Episode；DP方法则是基于Model（知道模型的运作方式）的计算状态价值的方法，它通过计算一个状态S所有可能的转移状态S’及其转移概率以及对应的即时奖励来计算这个状态S的价值。

• 关于是否Bootstrap：MC没有bootstrapping，只使用实际收获；DP和TD都有bootstrapping。

• 关于是否用采样来计算: MC和TD都是应用样本来估计实际的价值函数；而DP则是利用模型直接计算得到实际价值函数，没有采样之说。

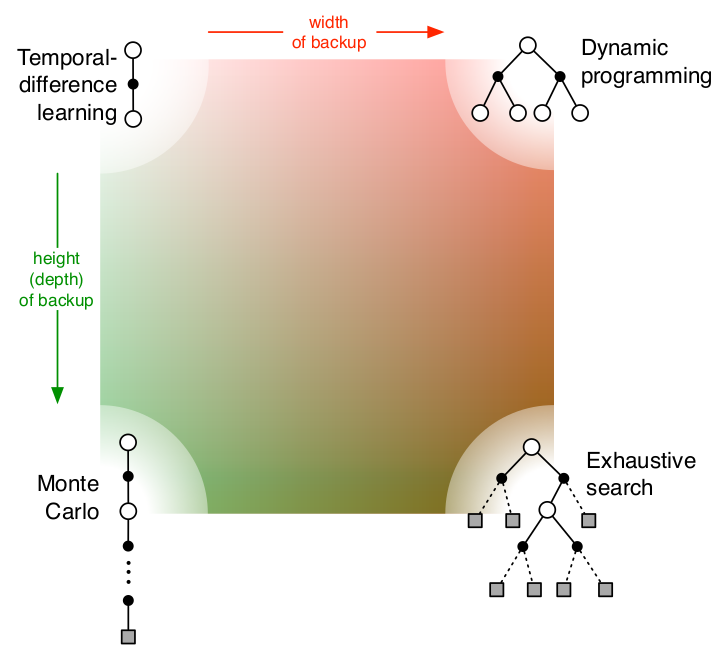
上图从两个维度解释了四种算法的差别，多了一个穷举法。这两个维度分别是：采样深度和广度。

• 当使用单个采样，同时不走完整个Episode就是TD；

• 当使用单个采样但走完整个Episode就是MC；

• 当考虑全部样本可能性，但对每一个样本并不走完整个Episode时，就是DP；

• 当既考虑所有样本，又把Episode从开始到终止遍历完，就变成了穷举法。

需要提及的是：DP利用的是整个MDP问题的模型，也就是状态转移概率，虽然它并不实际利用样本，但是它利用了整个模型的规律，因此认为是Full Width的。

bootstrapping

在前面的章节，我们一直提到bootstrapping这个名词，然而却没有解释它的含义，现在是时候了。

统计学中，bootstrapping可以指依赖于重置随机抽样的一切试验。bootstrapping可以用于计算样本估计的准确性。对于一个采样，我们只能计算出某个统计量(例如均值)的一个取值，无法知道均值统计量的分布情况。但是通过自助法(自举法)我们可以模拟出均值统计量的近似分布。有了分布很多事情就可以做了（比如说有你推出的结果来进而推测实际总体的情况）。

bootstrapping方法的实现很简单，假设抽取的样本大小为n，在原样本中有放回的抽样，抽取n次。每抽一次形成一个新的样本，重复操作，形成很多新样本，通过这些样本就可以计算出样本的一个分布。新样本的数量通常是1000-10000。如果计算成本很小，或者对精度要求比较高，就增加新样本的数量。

优点：简单易于操作。

缺点：bootstrapping的运用基于很多统计学假设，因此假设的成立与否会影响采样的准确性。

但是，这不是bootstrapping在RL中的含义！

Finally, we note one last special property of DP methods. All of them update estimates of the values of states based on estimates of the values of successor states. That is, they update estimates on the basis of other estimates. We call this general idea bootstrapping.

上面这段是Sutton给bootstrapping的定义，其实也不是太好懂。那么bootstrapping到底是什么意思呢？

\[V(S_t)\leftarrow V(S_t)+\alpha(R_{t+1}+\gamma V(S_{t+1})-V(S_t))\]

上式是TD的更新公式，从中可以看出TD target：\(R_{t+1}+\gamma V(S_{t+1})\)中已经包含了V(s)，也就是说它是用其它V(s)更新当前V(s)。这种特性就是bootstrapping。

\[V(S_t)\leftarrow V(S_t)+\alpha(G_t-V(S_t))\]

而MC的target：\(G_t\)就和V(s)无关。

参考：

https://datascience.stackexchange.com/questions/26938/what-exactly-is-bootstrapping-in-reinforcement-learning

What exactly is bootstrapping in reinforcement learning?

TD(n)

先前所介绍的TD算法实际上都是TD(0)算法，括号内的数字0表示的是在当前状态下往前多看1步，要是往前多看2步更新状态价值会怎样？这就引入了n-step的概念。

在当前状态往前行动n步，计算n步的return，同样TD target 也由2部分组成，已走的步数使用确定的即时reward，剩下的使用估计的状态价值替代。这就是TD(n)算法。

显然，MC实际上就是TD(\(n=\infty\))。

定义n-步收获：

\[G_t^{(n)}=R_{t+1}+\gamma R_{t+2}+\dots+\gamma^{n-1}R_{t+n}+\gamma^nV(S_{t+n})\]

TD(n)的更新公式：

\[V(S_t)\leftarrow V(S_t)+\alpha(G_t^{(n)}-V(S_t))\]

Large Random Walk

既然存在n-步预测，那么n=？时效果最好呢，下面的例子试图回答这个问题：

这个示例研究了使用多个不同步数预测联合不同步长(step-size，公式里的系数\(\alpha\)）时，分别在在线（On-line）和离线（Off-line）状态时状态函数均方差的差别。所有研究使用了10个Episode。离线与在线的区别在于，离线是在经历所有10个Episode后进行状态价值更新；而在线则至多经历一个Episode就更新一次状态价值。

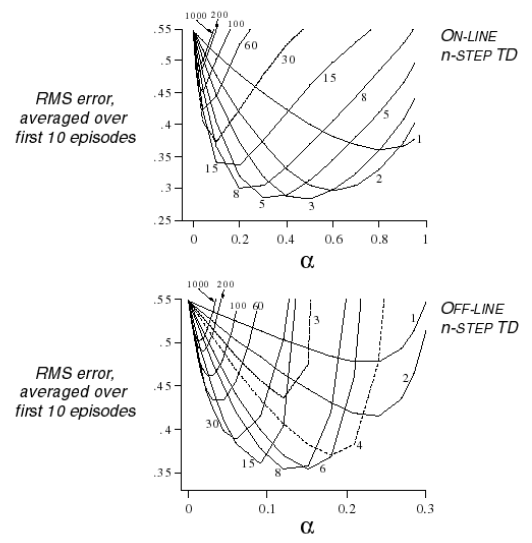
结果如上图所示，离线和在线之间曲线的形态差别不明显；从步数上来看，步数越长，越接近MC算法，均方差越大。对于这个大规模随机行走示例，在线计算比较好的步数是3-5步，离线计算比较好的是6-8步。但是不同的问题其对应的比较高效的步数不是一成不变的。因此选择多少步数作为一个较优的计算参数也是一个问题。

TD(\(\lambda\))

一种简单的方法是计算Averaging n-Step Returns，例如：

\[G=\frac{1}{2}G^{(2)}+\frac{1}{2}G^{(4)}\]

有没有更有效的方法呢？这里我们引入了一个新的参数：\(\lambda\)。通过引入这个新的参数，可以做到在不增加计算复杂度的情况下综合考虑所有步数的预测。

\(\lambda\)收获：

\[G_t^{\lambda}=(1-\lambda)\sum_{n=1}^\infty\lambda^{n-1}G_t^{(n)}\]

\(\lambda\)预测：

\[V(S_t)\leftarrow V(S_t)+\alpha(G_t^{\lambda}-V(S_t))\]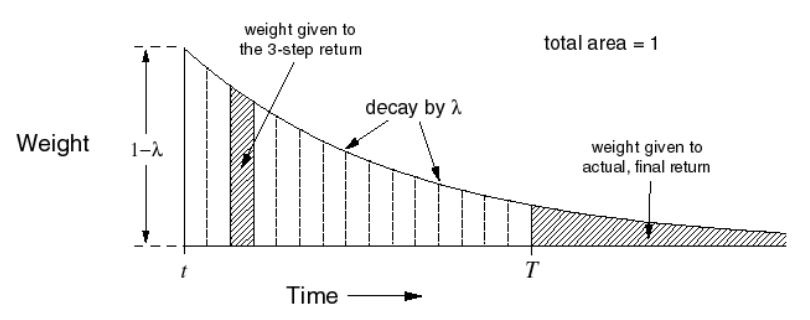

这张图还是比较好理解的，例如对于n=3的3-步收获，赋予其在收获中的权重如左侧阴影部分面积，对于终止状态的T-步收获，赋予其T以后的所有阴影部分面积。而所有节段面积之和为1。这种几何级数的设计也考虑了算法实现的计算方便性。

TD(\(\lambda\))的设计使得Episode中，后一个状态的状态价值与之前所有状态的状态价值有关，同时也可以说成是：一个状态价值参与决定了后续所有状态的状态价值。但是每个状态的价值对于后续状态价值的影响权重是不同的。我们可以从两个方向来理解TD(\(\lambda\))：

前向认识TD(\(\lambda\))

引入了\(\lambda\)之后，会发现要更新一个状态的状态价值，必须要走完整个Episode获得每一个状态的即时奖励以及最终状态获得的即时奖励。这和MC算法的要求一样，因此TD(\(\lambda\))算法有着和MC方法一样的劣势。λ取值区间为[0,1]，当\(\lambda\)=1时对应的就是MC算法。这给实际计算带来了不便。

反向认识TD(\(\lambda\))

TD(\(\lambda\))从另一方面提供了一个单步更新的机制，通过下面的示例来说明。

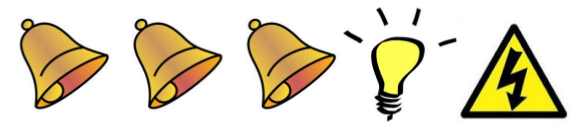
老鼠在连续接受了3次响铃和1次亮灯信号后遭到了电击，那么在分析遭电击的原因时，到底是响铃的因素较重要还是亮灯的因素更重要呢？

这里有两种启发方法：

频率启发 Frequency heuristic：将原因归因于出现频率最高的状态。

就近启发 Recency heuristic：将原因归因于较近的几次状态。

给每一个状态引入一个数值：效用追踪（Eligibility Traces, ET），来结合上述两种启发：

\[\begin{array}\\ E_0(s)=0\\ E_t(s)=\gamma\lambda E_{t-1}(s)+1(S_t=s) \end{array}\]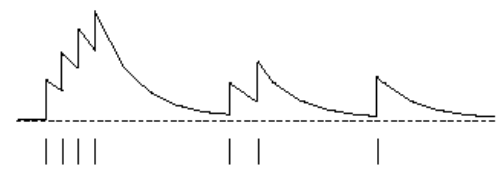

上图是\(E_t(s)\)函数的一个可能的曲线图。该图横坐标是时间，横坐标下有竖线的位置代表当前进入了状态s，纵坐标是效用追踪值E 。可以看出当某一状态连续出现，E值会在一定衰减的基础上有一个单位数值的提高，此时将增加该状态对于最终收获贡献的比重，因而在更新该状态价值的时候可以较多地考虑最终收获的影响。同时如果该状态距离最终状态较远，则其对最终收获的贡献越小。

特别的，E值并不需要等到完整的Episode结束才能计算出来，它可以每经过一个时刻就得到更新。E值存在饱和现象，有一个瞬时最高上限：

\[E_\max=1/(1-\gamma\lambda)\]