ML » 机器学习(三十)——概率图模型, HMM
2018-01-07 :: 5175 Words概率图模型
资料
probabilistic graphical model(PGM)最早由Judea Pearl发明。
这方面比较重要的文章和书籍有:
http://www.cis.upenn.edu/~mkearns/papers/barbados/jordan-tut.pdf
Michael Irwin Jordan著。
《Probabilistic Graphical Models: Principles and Techniques》,Daphne Koller,Nir Friedman著(2009年)。
Judea Pearl,1936年生,以色列-美国计算机科学家,UCLA教授。2011年获得图灵奖。
Michael Irwin Jordan,1956年生,美国计算机科学家。UCSD博士,先后执教于MIT和UCB。吴恩达的导师。
Daphne Koller,女,1968年生,以色列-美国计算机科学家。斯坦福大学博士及教授。和吴恩达共同创立在线教育平台Coursera。
Nir Friedman,1967年生,以色列计算机科学家。斯坦福大学博士,耶路撒冷希伯来大学教授。
http://www.cs.cmu.edu/~epxing/Class/10708-14/lectures/
CMU的邢波(Eric Xing)所开的概率图模型课程。
概述
概率图模型的三要素:Graph:\(\mathcal{G}\)、Model:\(\mathcal{M}\)和Data:\(\mathcal{D}\equiv\{X^{(i)}_1,\dots,X^{(i)}_m\}^N_{i=1}\)。
它要解决的三大问题:
1.表示。如何获取或定义真实世界的不确定度?如何对领域知识/假设/约束编码?
2.推断。根据模型/数据,推断答案。
\[\text{e.g.}:P(x_i\mid \mathcal{D})\]3.学习。根据数据确定哪个模型是正确的。
\[\text{e.g.}:\mathcal{M}=\arg\max_{\mathcal{M}\in M}F(\mathcal{D};\mathcal{M})\]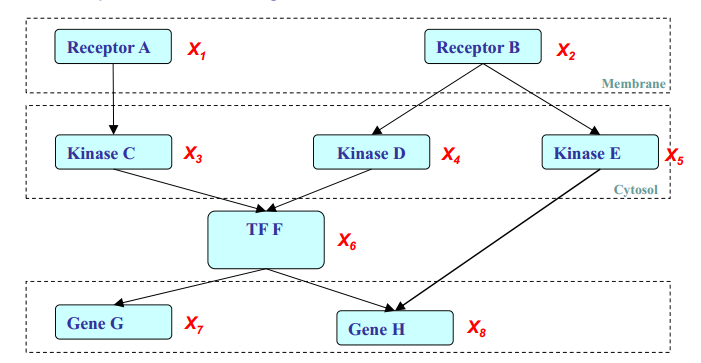
上图是PGM的一个示例。其中\(X_i\)表示随机变量,图中共有8个随机变量,假设它们均为二值变量,则整个状态空间共有\(2^8\)种组合。遍历这样大的状态空间无疑是一件极为费力的事情。
如果\(X_i\)是条件独立的话,则由上图可得:
\[\begin{array}\\ P(X_1,\dots,X_8)=P(X_2)P(X_4\mid X_2)P(X_5\mid X_2)P(X_1)P(X_3\mid X_1)\\ P(X_6\mid X_3,X_4)P(X_7\mid X_6)P(X_8\mid X_5,X_6) \end{array}\]这样,状态空间就缩小为\(2+4+4+2+4+8+4+8=36\)种组合了。
根据边的类型,PGM可分为两类:
1.有向边表示变量间的因果关系(单向依赖)。这样的PGM,常称为Bayesia Network(BN)或Directed Graphical Model(DGM)。
2.无向边表示变量间的相关关系(互相依赖)。这样的PGM,常称为Markov Random Field(MRF)或Undirected Graphical Model(UGM)。
因果关系是一种强逻辑关系,需要变量间有深刻的内在联系。而相关关系要弱的多,典型的例子就是《机器学习(十七)》中的尿布和啤酒的故事。尿布和啤酒虽然正相关,然而它们本身却没有多大的联系。
根据模型的不同,PGM又可分为生成模型(Generative Model, GM)和判别模型(Discriminative Model, DM)。两者的区别在《机器学习(三)》中已经简单提到过,这里做一个扩展。
之前提到的机器学习算法,主要是建立特征向量X和标签Y之间的联系。但是实际情况下,X中的状态不一定都能得到,因此可以根据可见性,将X分为可观测变量集合O和其他变量集合R,Y也不一定是一个标签,而可能是一个变量集合。即:
\[GM:P(Y,R,O)\to P(Y\mid O)\] \[DM:P(Y,R\mid O)\to P(Y\mid O)\]注意,在贝叶斯学派的观点中,模型的参数也是随机变量,因此,R在某些情况下,不仅包含不可观测的变量,也包含模型参数。
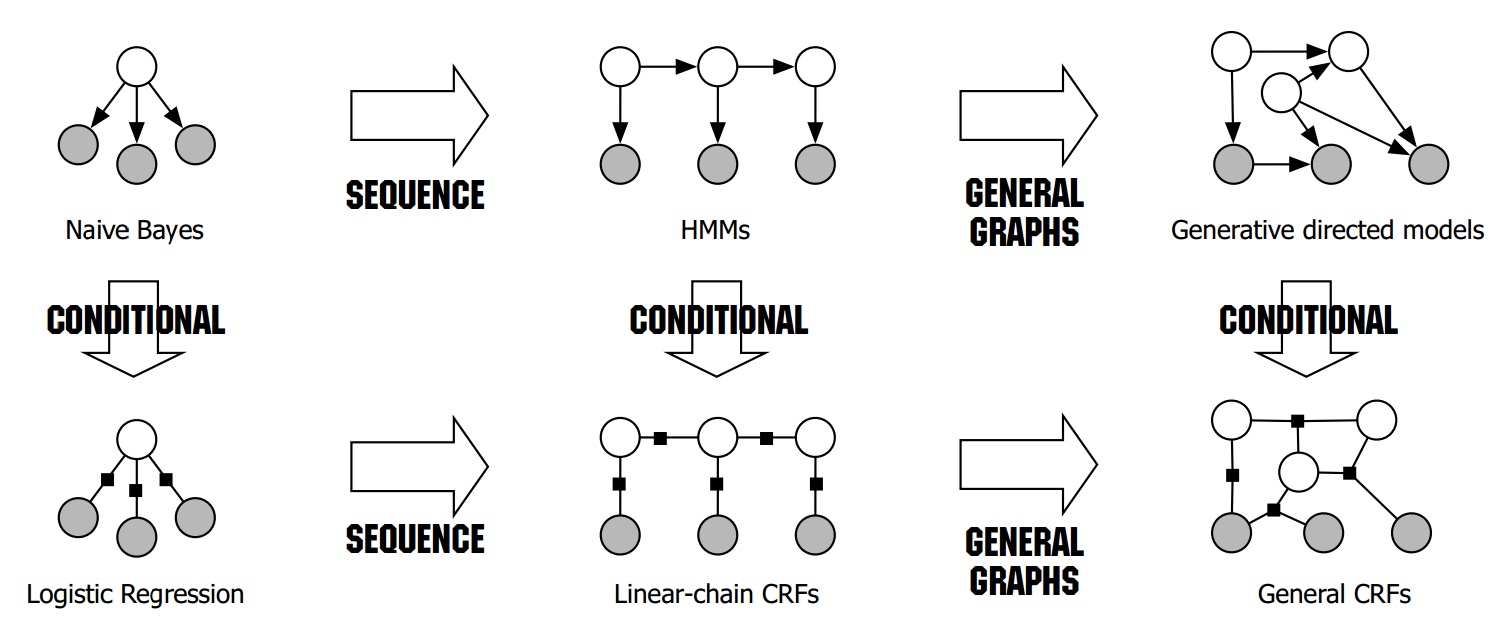
上图是按照GM/DM标准进行分类的各主要PGM的关系图。其中上一行是GM,而下一行是DM。
概率图模型的图形表示法
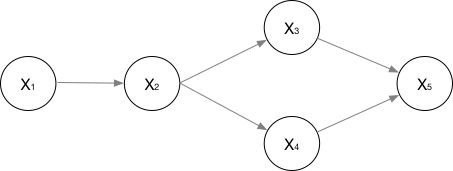
上图是一个有向概率图模型的示意图。其中结点表示变量,边表示变量之间的依赖关系,箭头表示了依赖关系的方向。以上图为例,\(x_2\)依赖于\(x_1\)。
贝叶斯网络
贝叶斯网络是最简单的有向图模型。
首先给出几个术语:
有向无环图(Directed Acyclic Graph, DAG)
下图是图模型的部分变种之间的关系图。
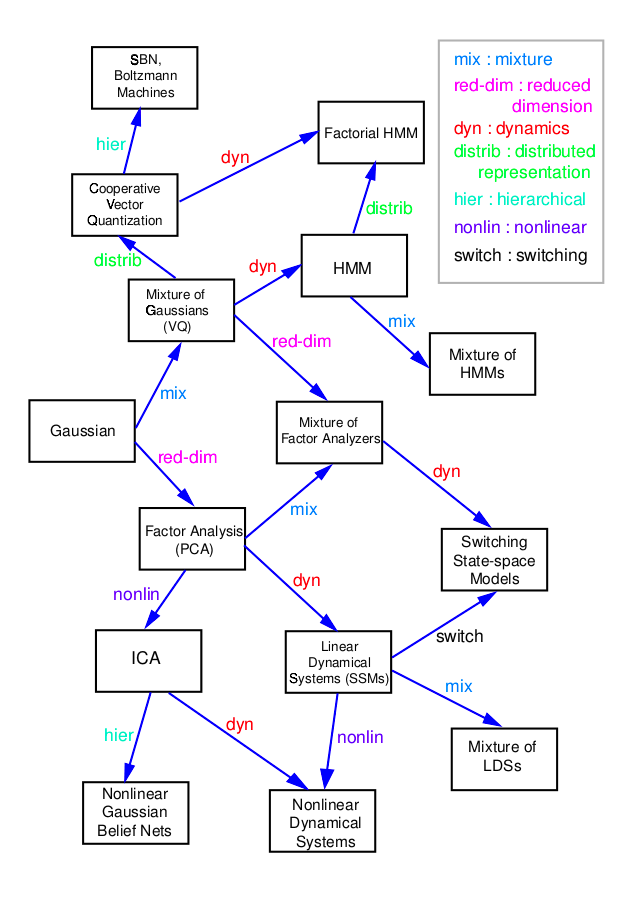
参考
https://mp.weixin.qq.com/s/srLs_88QOFkBiKMiLZH9HA
想了解概率图模型?你要先理解图论的基本定义与形式
https://mp.weixin.qq.com/s/S-6Mb6zNzVPpxR8DbWdT-A
读懂概率图模型:你需要从基本概念和参数估计开始
https://mp.weixin.qq.com/s/b_0sxD0noWnuIkCxxUBlDA
终极入门:马尔可夫网络 (Markov Networks)
https://mp.weixin.qq.com/s/QvD97vfnv1x8w-e33WymRA
从贝叶斯理论到图像马尔科夫随机场
https://mp.weixin.qq.com/s/fTyaRMXtw2Hz99WKJ7WWfQ
因果图,Causal Graphs,52页ppt
https://mp.weixin.qq.com/s/LpUj_nyxK0_V2edcucJ2iQ
概率图模型笔记(PART I)
https://mp.weixin.qq.com/s/gOgH-tsQTp7ijOWqpAJi_Q
概率图模型笔记(PART II)隐马尔科夫模型
https://mp.weixin.qq.com/s/2Uh_PgQp7hqk8IrFQzthQw
概率图模型笔记(PART III)条件随机场简介
https://mp.weixin.qq.com/s/1V-AVzAZtKTLHejAo-4OAA
用Python构建概率图模型,173页pdf
HMM
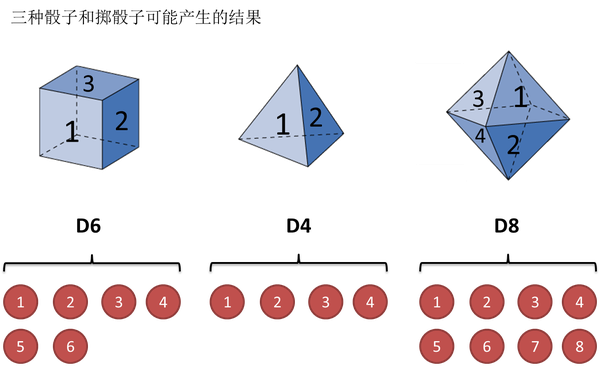
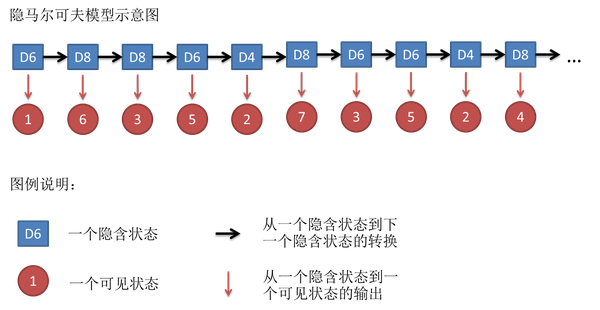
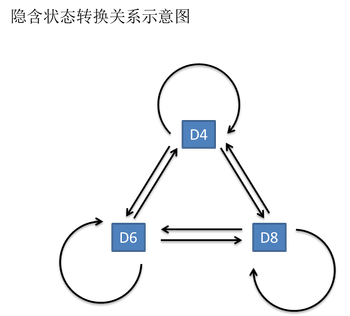
上图中的隐含状态,也称states。可见状态,也称observations。黑线被称为transition probability,而红线则是emission probability或output probability。第一个observations的概率被称为start probability。
因此一个HMM可以表示为:
\[\mu=(A,B,\pi)\]其中,A是transition probability,B是emission probability,\(\pi\)是start probability。
A、B、\(\pi\)加上可见状态X、隐含状态Y,就构成了HMM的5要素。
如果可见状态和隐含状态之间,存在一对一的关系,那么HMM就退化成普通的Markov链了。
和HMM(Hidden Markov Model,隐马尔可夫模型)模型相关的算法主要分为三类,分别解决三种问题:
1)知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种骰子(隐含状态链)。
这个问题呢,在语音识别领域呢,叫做解码问题。这个问题其实有两种解法,会给出两个不同的答案。每个答案都对,只不过这些答案的意义不一样。第一种解法求最大似然状态路径,说通俗点呢,就是我求一串骰子序列,这串骰子序列产生观测结果的概率最大。第二种解法呢,就不是求一组骰子序列了,而是求每次掷出的骰子分别是某种骰子的概率。比如说我看到结果后,我可以求得第一次掷骰子是D4的概率是0.5,D6的概率是0.3,D8的概率是0.2。
2)知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。
看似这个问题意义不大,因为你掷出来的结果很多时候都对应了一个比较大的概率。问这个问题的目的呢,其实是检测观察到的结果和已知的模型是否吻合。如果很多次结果都对应了比较小的概率,那么就说明我们已知的模型很有可能是错的,有人偷偷把我们的骰子給换了。问题2的更一般的用法是:从若干种模型中选择一个概率最大的模型。
3)知道骰子有几种(隐含状态数量),不知道每种骰子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种骰子是什么(转换概率)。
这个问题很重要,因为这是最常见的情况。很多时候我们只有可见结果,不知道HMM模型里的参数,我们需要从可见结果估计出这些参数,这是训练建模的一个必要步骤。
参考:
https://www.zhihu.com/question/20962240
如何用简单易懂的例子解释隐马尔可夫模型?
http://www.cnblogs.com/kaituorensheng/archive/2012/11/29/2795499.html
隐马尔可夫模型
https://mp.weixin.qq.com/s/9MmHDVDal57pdotwxAn_uQ
HMM模型详解
https://mp.weixin.qq.com/s/PzPRKZa1C5IlEUASWt71cA
从朴素贝叶斯到维特比算法:详解隐马尔科夫模型
https://mp.weixin.qq.com/s/aIpRx-etMkh7jwL2lFNa4w
理解隐马尔可夫模型
https://mp.weixin.qq.com/s/O0oAzJ-Hk9pQkojgdgT4qg
隐马尔可夫模型
https://mp.weixin.qq.com/s/RcMtaBdB2zsmZlVfiM11xA
用于语音识别、分词的隐马尔科夫模型HMM
https://mp.weixin.qq.com/s/6BnCJKHU2krEvizEQczuaQ
一站式解决:隐马尔可夫模型(HMM)全过程推导及实现
Viterbi算法
Viterbi算法是求解最大似然状态路径的常用算法,被广泛应用于通信(CDMA技术的理论基础之一)和NLP领域。
Andrew James Viterbi,1935年生,意大利裔美国工程师、企业家,高通公司联合创始人。MIT本硕+南加州大学博士。viterbi算法和CDMA标准的主要发明人。
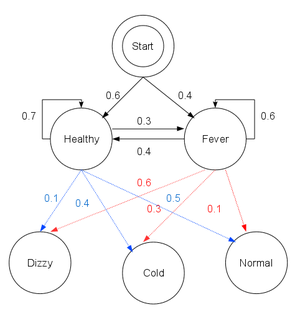
上图是一个HMM模型的概率图表示,其中{‘Healthy’,’Fever’}是隐含状态,而{‘normal’,’cold’,’dizzy’}是可见状态,边是各状态的转移概率。
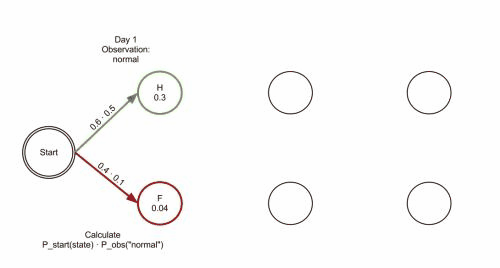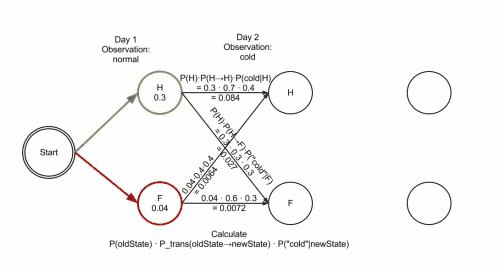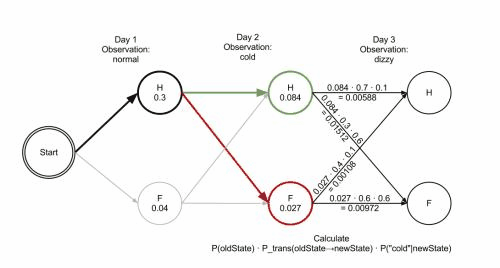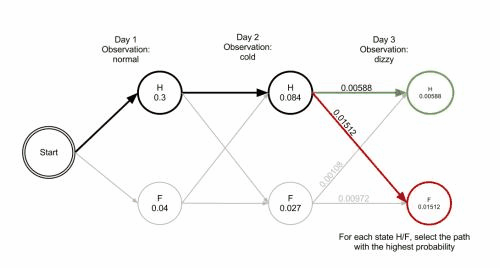
上图是Viterbi算法的动画图。简单来说就是:从开始状态之后每走一步,就记录下到达该状态的所有路径的概率最大值,然后以此最大值为基准继续向后推进。显然,如果这个最大值都不能使该状态成为最大似然状态路径上的结点的话,那些小于它的概率值(以及对应的路径)就更没有可能了。
Viterbi算法只能求出最佳路径,对于N-best问题就需要进行扩展方可。
参考:
https://mp.weixin.qq.com/s/FQ520ojMmbFhNMoNCVTKug
通俗理解维特比算法
https://www.zhihu.com/question/20136144
谁能通俗的讲解下viterbi算法?
https://mp.weixin.qq.com/s/xyWY3Z5PiHkCFzCP0noBvA
一文读懂HMM模型和Viterbi算法
https://zhuanlan.zhihu.com/p/110007411
维特比算法的直观解释——最短路径视角
前向算法
forward算法是求解问题2的常用算法。
仍以上面的掷骰子为例,要算用正常的三个骰子掷出这个结果的概率,其实就是将所有可能情况的概率进行加和计算。同样,简单而暴力的方法就是把穷举所有的骰子序列,还是计算每个骰子序列对应的概率,但是这回,我们不挑最大值了,而是把所有算出来的概率相加,得到的总概率就是我们要求的结果。

您的打赏,是对我的鼓励
