ML » 机器学习(三十七)——时间序列分析(1), 辛普森悖论
2018-06-08 :: 6209 Words时间序列分析
书籍和教程
http://www.stat.berkeley.edu/~bartlett/courses/153-fall2010/
berkeley的时间序列分析课程
http://people.duke.edu/%7Ernau/411home.htm
回归和时间序列分析
《应用时间序列分析》,王燕著。
https://mp.weixin.qq.com/s/w_u6_lG-_b0t4m4YubjeRQ
最新《时间序列分析》课程笔记,477页pdf
https://mp.weixin.qq.com/s/8Ua7wYfRdv0fu8I-M3sdHg
统计学习与序列预测,261页pdf
https://mp.weixin.qq.com/s/J3RdKXZs7Wb976E512TJjw
最新《时序数据分析》书稿,512页pdf
概述
时间序列,就是按时间顺序排列的,随时间变化的数据序列。
生活中各领域各行业太多时间序列的数据了,销售额,顾客数,访问量,股价,油价,GDP,气温…
随机过程的特征有均值、方差、协方差等。
如果随机过程的特征随着时间变化,则此过程是非平稳的;相反,如果随机过程的特征不随时间而变化,就称此过程是平稳的。
下图所示,左边非稳定,右边稳定。
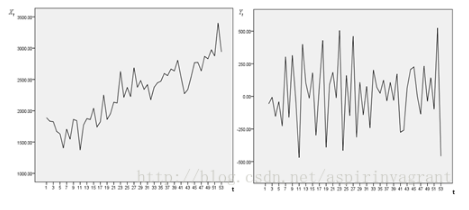
非平稳时间序列分析时,若导致非平稳的原因是确定的,可以用的方法主要有趋势拟合模型、季节调整模型、移动平均、指数平滑等方法。
若导致非平稳的原因是随机的,方法主要有ARIMA及自回归条件异方差模型等。
ARIMA
ARIMA模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA),也叫求和自回归移动平均模型,是由George Edward Pelham Box和Gwilym Meirion Jenkins于70年代初提出的一著名时间序列预测方法,所以又称为box-jenkins模型、博克思-詹金斯法。
Gwilym Meirion Jenkins,1932~1982,英国统计学家。伦敦大学学院博士,兰卡斯特大学教授。
同《数学狂想曲(十一)》中的PID算法一样,ARIMA模型实际上是三个简单模型的组合。
AR模型
\[X_t = c + \sum_{i=1}^p \varphi_i X_{t-i}+ \varepsilon_t\]其中,p为阶数,\(\varepsilon_t\)为白噪声。上式又记作AR(p)。显然,AR模型是一个系统状态模型。
MA模型
\[X_t = \mu + \varepsilon_t + \sum_{i=1}^q \theta_i \varepsilon_{t-i}\]上式记作MA(q),其中q和\(\varepsilon_t\)的含义与上同。MA模型是一个噪声模型。
ARMA模型
AR模型和MA模型合起来,就是ARMA模型:
\[X_t = c + \varepsilon_t + \sum_{i=1}^p \varphi_i X_{t-i} + \sum_{i=1}^q \theta_i \varepsilon_{t-i}\]同理,上式也被记作ARMA(p,q)。
Lag operator
在继续下面的描述之前,我们先来定义一下Lag operator–L。
\[L X_t = X_{t-1} \; \text{or} \; X_t = L X_{t+1}\]I模型
\[(1-L)^d X_t\]上式中d为阶数,因此上式也记作I(d)。显然\(I(0)=X_t\)。
I模型有什么用呢?我们观察一下I(1):
\[(1-L) X_t = X_t - X_{t-1} = \Delta X\]有的时候,虽然I(0)不是平稳序列,但I(1)是平稳序列,这时我们称该序列是1阶平稳序列。n阶的情况,可依此类推。
ARIMA模型
ARIMA模型可以看作是两个随机过程的组合。
首先是非平稳过程:
\[Y_t = (1-L)^d X_t\]接着是一个广义平稳过程:
\[\left( 1 - \sum_{i=1}^p \phi_i L^i \right) Y_t = \left( 1 + \sum_{i=1}^q \theta_i L^i \right) \varepsilon_t\]最后得到ARIMA模型的公式:
\[\left( 1 - \sum_{i=1}^p \phi_i L^i\right) (1-L)^d X_t = \delta + \left( 1 + \sum_{i=1}^q \theta_i L^i \right) \varepsilon_t\]上式也被记作ARIMA(p,d,q)。从上式可以看出,ARIMA模型实际上就是利用I模型,将时间序列转化为平稳序列之后的ARMA模型。
上面的内容只是对ARIMA模型给出一个简单的定义。实际的假设检验、参数估计的步骤,还是比较复杂的,完全可以写本书来说。
其它
除了ARIMA系列模型之外,ARCH系列模型也用的比较多:
autoregressive conditional heteroskedasticity, ARCH
generalized autoregressive conditional heteroskedasticity, GARCH
上面介绍的序列建模方法主要针对的是:预测未来节点,即所谓的走势分析问题。
时间序列的常见问题还包括:
-
判断不同序列类别,即序列分类问题。
-
不同时序对应的状态的分析,即序列标注问题。
这些问题的常见工具包括HMM、CRF、RNN等,可参见其他相关章节。
参考:
https://mp.weixin.qq.com/s/LAn9h6_WkxlZ_IsrhnzZCw
波动率建模之ARCH模型
工具
http://mp.weixin.qq.com/s/ioaS7RQ6bsJs4_X0G4ZHyQ
如何优雅地用TensorFlow预测时间序列:TFTS库详细教程
https://mp.weixin.qq.com/s/7WuB0uvGSAek9b4TP_0r9g
内置降维、聚类等算法,时间序列数据分析Python库Deeptime
https://zhuanlan.zhihu.com/p/391897734
FaceBook开源全网第一个时序王器Kats
https://mp.weixin.qq.com/s/XCHSulXn1hzgLqLJjXkSGg
TODS:从时间序列数据中检测不同类型的异常值
Prophet
Prophet是FaceBook提出的时间序列算法。同时,也是该算法的工具包的名字。
官网:
https://facebook.github.io/prophet/
参考:
https://mp.weixin.qq.com/s/ven_4JbWYFswIkGyhjTcww
Prophet:教你如何用加法模型探索时间序列数据
https://mp.weixin.qq.com/s/PMsAjk7WbGRu2n3s6Q8prQ
Facebook时间序列预测算法Prophet的研究
https://mp.weixin.qq.com/s/bf_CHcoZMjqP6Is4ebD58g
使用Prophet预测股价并进行多策略交易
https://mp.weixin.qq.com/s/pJTDJrMCfv5y4LQ2itt1tQ
Facebook的Prophet算法简介与使用
https://mp.weixin.qq.com/s/675ASxDSVH_8BX6W8WRRqg
基于Prophet的时间序列预测
https://mp.weixin.qq.com/s/4rJL3cccsjVqgrNDjcMIJw
Prophet:Facebook创造的先知
https://mp.weixin.qq.com/s/Ylvk3IqSWRD2K_AXMZwnoA
手把手教你用Python的Prophet库进行时间序列预测
https://mp.weixin.qq.com/s/fMkxWLGSKQm_3fyfLgbQew
详解Prophet模型以及代码示例
https://mp.weixin.qq.com/s/s3R-_cuTYR7Z8w9DhlxifQ
NeuralProphet:基于神经网络的时间序列建模库
Lebesgue积分
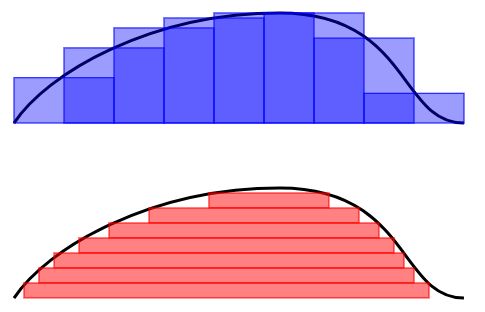
蓝色的是Riemann积分,红色的是Lebesgue积分。
Henri Léon Lebesgue,1875~1941,法国数学家。
参考:
https://zhuanlan.zhihu.com/p/34407471
如何理解时间序列?—从Riemann积分和Lebesgue积分谈起
https://zhuanlan.zhihu.com/p/49262150
从Riemann积分到Lebesgue积分
https://zhuanlan.zhihu.com/p/90607361
Quadrature求积法
https://zhuanlan.zhihu.com/p/91709767
ODE’s Initial value problem (IVP)
参考
https://en.wikipedia.org/wiki/Autoregressive_integrated_moving_average
https://en.wikipedia.org/wiki/Autoregressive%E2%80%93moving-average_model
https://zhuanlan.zhihu.com/p/23534595
时间序列分析:结合ARMA的卡尔曼滤波算法(该文的参考文献中有不少好文)
https://www.zhihu.com/question/337447961
时间序列和回归分析有什么本质区别?
http://blog.csdn.net/aliceyangxi1987/article/details/71079522
用ARIMA模型做需求预测
http://blog.csdn.net/kicilove/article/details/78315335
时间序列初级理论篇
https://mp.weixin.qq.com/s/Y342U71oicbpJbWl4E0ZEQ
时间序列基本概念
https://mp.weixin.qq.com/s/K-XGuaWTcF6BDPJagaJDPQ
时序数据与事件的关联分析
https://mp.weixin.qq.com/s/JR-GIXwHF45OysoE0qvwzw
时间序列异常检测机制的研究
https://mp.weixin.qq.com/s/MYwvuD85PPs3PJA5tMxvgw
6种时序异常检测思路总结!(tsod)
https://mp.weixin.qq.com/s/2hpQ_7Ih58d1RKYb1oW_Sg
时间序列简介(一)
https://zhuanlan.zhihu.com/p/35093835
时间序列的自回归模型—从线性代数的角度来看
https://zhuanlan.zhihu.com/p/39105270
时间序列的表示与信息提取
https://mp.weixin.qq.com/s/iah8PvIC0oZngSaNHw7gJw
从上帝视角看透时间序列和数据挖掘
https://zhuanlan.zhihu.com/p/38130622
时间序列的相似性
https://mp.weixin.qq.com/s/DGGuAYsoa6DPD6FBf2Hc4g
时间序列分析之理论篇
https://zhuanlan.zhihu.com/p/50698719
两篇关于时间序列的论文
https://zhuanlan.zhihu.com/p/55129654
时间序列的单调性
https://zhuanlan.zhihu.com/p/55903495
时间序列的聚类
https://mp.weixin.qq.com/s/2teyejpbpM6x5UCiYL8s-Q
关于时间序列你需要了解的一切
https://mp.weixin.qq.com/s/Aqh9lZvyDncyCdXgxH1lSQ
短小时序,如何预测?——基于特征重构的张量ARIMA
https://mp.weixin.qq.com/s/NHwMVzZWOU24pdbjzcchAg
从AR到ARIMA
https://mp.weixin.qq.com/s/QZ_AcfzuB7JQEE6cDz5G1A
自回归模型
https://mp.weixin.qq.com/s/fYQwRJGrTlX4_GqMt_CYMQ
时间序列基础教程总结
https://mp.weixin.qq.com/s/f0BwjlsEBlFVDxNlZqgf-g
Python时间序列分析:一项基于案例的全面指南
辛普森悖论
辛普森悖论为英国统计学家E.H.Simpson于1951年提出的悖论,即在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论。
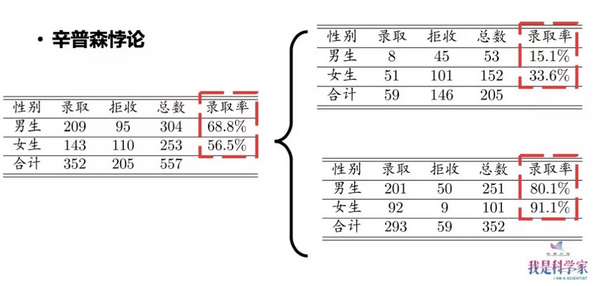
如果分专业来看,你就会发现:在各个专业女生的录取率其实都是更高的。之所以会产生“总体录取率女生偏低”这一结果,是因为女生大部分都报考了那些本身就难以录取的学院,而男生则大部分报考了那些录取率本身就偏高的学院。
参考:
https://mp.weixin.qq.com/s/5jZ2dzLInLtUw7rWZF4mtg
张忠元:渣男受女生欢迎?当心统计陷阱
https://mp.weixin.qq.com/s/o1a2YlYritcOrsLN2YuLmA
神奇的霍特林法则:为什么汉堡王总是开在麦当劳旁边?
https://mp.weixin.qq.com/s/eq4MllJta5NmaLARPpvang
公交车总迟到?你大概掉进了“等待时间悖论”
https://zhuanlan.zhihu.com/p/43934918
诡异的布雷斯悖论:为什么越是修新路,城市反而更堵了!
https://mp.weixin.qq.com/s/-0VMucGBq4Trb_9FnsW6KQ
10大反直觉的数学结论
https://mp.weixin.qq.com/s/FqY19sTQd7GPdGSsB5L9eQ
数学大反例合集
https://mp.weixin.qq.com/s/EICefFM3dfv5A6V9kVqGWw
吸烟致癌的迷思是如何破除的
https://mp.weixin.qq.com/s/NlJ4-b5SjIjPGgvLUuSxFw
孩子,有时候并不是生活欺骗了你,而是你可能还不懂概率统计……

您的打赏,是对我的鼓励
