ML » 机器学习(二十)——Loss function详解
2017-03-04 :: 7140 Words关联规则挖掘
关联规则评价(续)
确信度
Conviction的定义如下:
\[\mathrm{conv}(X\Rightarrow Y) =\frac{ 1 - \mathrm{supp}(Y) }{ 1 - \mathrm{conf}(X\Rightarrow Y)}\]它的值越大,表明X、Y的独立性越小。
全自信度
\[\begin{array}\\ all\_confidence(A,B)=\frac{P(A\cap B)}{max\{P(A),P(B)\}}\\ =min\{P(B|A),P(A|B)\}=min\{confidence(A\to B),confidence(B\to A)\} \end{array}\]最大自信度
\[max\_confidence(A,B)=max\{confidence(A\to B),confidence(B\to A)\}\]Kulc
\[kulc(A,B)=\frac{confidence(A\to B)+confidence(B\to A)}{2}\]cosine距离
\[\begin{array}\\ cosine(A,B)=\frac{P(A\cap B)}{sqrt(P(A)*P(B))}=sqrt(P(A|B)*P(B|A))\\ =sqrt(confidence(A\to B)*confidence(B\to A)) \end{array}\]Leverage
\[Leverage(A,B) = P(A\cap B)-P(A)P(B)\]不平衡因子
imbalance ratio的定义:
\[IR(A,B)=\frac{|support(A)-support(B)|}{(support(A)+support(B)-support(A\cap B))}\]全自信度、最大自信度、Kulc、cosine,Leverage是不受空值影响的,这在处理大数据集是优势更加明显,因为大数据中空记录更多,根据分析我们推荐使用kulc准则和不平衡因子结合的方法。
参考:
http://www.cnblogs.com/fengfenggirl/p/associate_measure.html
关联规则评价
https://mp.weixin.qq.com/s/s1Snb4XnIQk1DcK3nESilw
PrefixSpan算法原理详解
Loss function详解
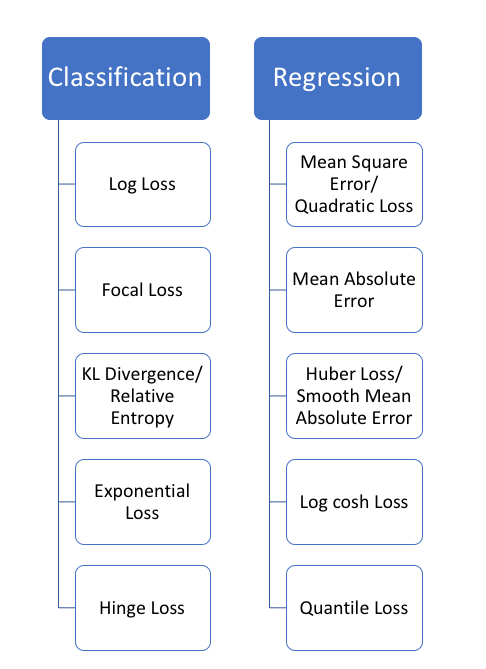
Mean Squared Error(MSE)/Mean Squared Deviation(MSD)
\[\operatorname{MSE}=\frac{1}{n}\sum_{i=1}^n(\hat{Y_i} - Y_i)^2\]Symmetric Mean Absolute Percentage Error(SMAPE or sMAPE)
MSE定义的误差,实际上是向量空间中的欧氏距离,这也可称为绝对误差。而有些情况下,可能相对误差(即百分比误差)更有意义些:
\[\text{SMAPE} = \frac 1 n \sum_{t=1}^n \frac{\left|F_t-A_t\right|}{(A_t+F_t)/2}\]上式的问题在于\(A_t+F_t\le 0\)时,该值无意义。为了解决该问题,可用如下变种:
\[\text{SMAPE} = \frac{100\%}{n} \sum_{t=1}^n \frac{|F_t-A_t|}{|A_t|+|F_t|}\]参考:
https://mp.weixin.qq.com/s/TyjA2M_-gKO1Hm1jLRetZg
MAPE与sMAPE的优缺点
Mean Absolute Error(MAE)
\[\mathrm{MAE} = \frac{1}{n}\sum_{i=1}^n \left| f_i-y_i\right| =\frac{1}{n}\sum_{i=1}^n \left| e_i \right|\]这个可以看作是MSE的1范数版本。
Mean Percentage Error(MPE)
\[\text{MPE} = \frac{100\%}{n}\sum_{t=1}^n \frac{a_t-f_t}{a_t}\]不同的loss函数有不同的用途,比如softmax一般用Cross Entropy作为loss函数。如下图所示:
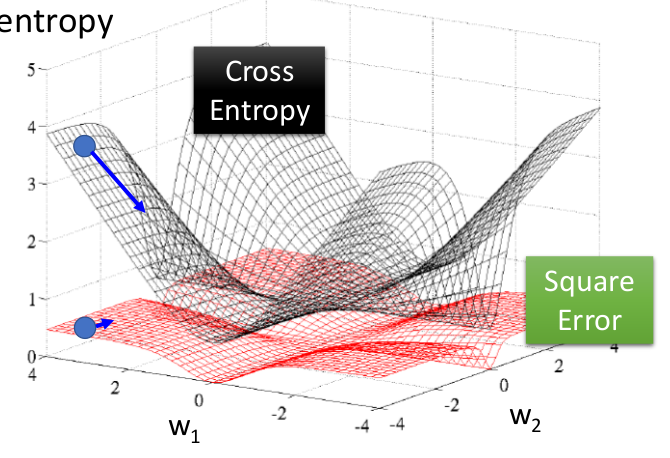
loss function比较
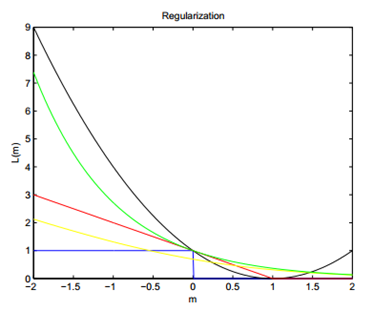
这里m代表了置信度,越靠近右边置信度越高。
其中蓝色的阶跃函数又被称为Gold Standard,黄金标准,因为这是最准确无误的分类器loss function了。分对了loss为0,分错了loss为1,且loss不随到分界面的距离的增加而增加,也就是说这个分类器非常鲁棒。但可惜的是,它不连续,求解这个问题是NP-hard的,所以才有了各种我们熟知的分类器。
其中红色线条就是SVM了,由于它在m=1处有个不可导的转折点,右边都是0,所以分类正确的置信度超过一定的数之后,对分界面的确定就没有一点贡献了。
《机器学习(五)》中提到的SVM软间隔,其所使用的loss function,又被称为Hinge loss函数:
\[l_{hinge}(z)=\max(0,1-z)\]除此之外,exponential loss函数:
\[l_{exp}(z)=\exp(-z)\]和logistic loss函数:
\[l_{log}(z)=\log(1+\exp(-z))\]也是较常用的SVM loss function。
黄色线条是Logistic Regression的损失函数,与SVM不同的是,它非常平滑,但本质跟SVM差别不大。
绿色线条是boost算法使用的损失函数。
黑色线条是ELM(Extreme learning machine)算法的损失函数。它的优点是有解析解,不必使用梯度下降等迭代方法,可直接计算得到最优解。但缺点是随着分类的置信度的增加,loss不降反升,因此,最终准确率有限。此外,解析算法相比迭代算法,对于大数据的适应较差,这也是该方法的局限所在。
参见:
https://www.zhihu.com/question/28810567
Extreme learning machine(ELM)到底怎么样,有没有做的前途?
Softmax详解
首先给出Softmax function的定义:
\[y_c=\zeta(\textbf{z})_c = \dfrac{e^{z_c}}{\sum_{d=1}^C{e^{z_d}}} \text{ for } c=1, \dots, C\]从中可以很容易的发现,如果\(z_c\)的值过大,朴素的直接计算会上溢出或下溢出。
解决办法:
\[z_c\leftarrow z_c-a,a=\max\{z_1,\dots,z_C\}\]证明:
\[\zeta(\textbf{z-a})_c = \dfrac{e^{z_c}\cdot e^{-a}}{\sum_{d=1}^C{e^{z_d}\cdot e^{-a}}} = \dfrac{e^{z_c}}{\sum_{d=1}^C{e^{z_d}}} = \zeta(\textbf{z})_c\]Softmax的损失函数是cross entropy loss function:
\[\xi(X, Y) = \sum_{i=1}^n \xi(\textbf{t}_i, \textbf{y}_i) = - \sum_{i=1}^n \sum_{i=c}^C t_{ic} \cdot \log(y_{ic})\]Softmax + cross entropy loss function的反向传播算法:
\[\begin{align} \dfrac{\partial\xi}{\partial z_i} &= - \sum_{j=1}^C \dfrac{\partial t_j \log(y_j)}{\partial z_i} \\ &= - \sum_{j=1}^C t_j \dfrac{\partial \log(y_j)}{\partial z_i} \\ &= - \sum_{j=1}^C t_j \dfrac{1}{y_j} \dfrac{\partial y_j}{\partial z_i} \\ &= - \dfrac{t_i}{y_i} \dfrac{\partial y_i}{\partial z_i} - \sum_{j \neq i}^C \dfrac{t_j}{y_j} \dfrac{\partial y_j}{\partial z_i} \\ &= - \dfrac{t_i}{y_i} y_i(1-y_i) - \sum_{j \neq i}^{C} \dfrac{t_j}{y_j}(-y_jy_j) \\ &= -t_i + t_iy_i + \sum_{j \neq i}^{C} t_jy_i \\ &= -t_i + \sum_{j=1}^C t_jy_i \\ &= -t_i + y_i \sum_{j=1}^C t_j \\ &= y_i - t_i \end{align}\]但是遗憾的是,由于Loss中可能存在正则项,直接用这个的机会并不多。
常用的还是Softmax自己的反向传播算法:
\[\nabla e_{(x)} = \nabla e_{(s)} \begin{bmatrix} -s_{1}s_{1} + s_{1} & -s_{1}s_{2} & \cdots & -s_{1}s_{k} \\ -s_{2}s_{1} & -s_{2}s_{2} + s_{2} & \cdots & -s_{2}s_{k} \\ \vdots & \vdots & \ddots & \vdots \\ -s_{k}s_{1} & -s_{k}s_{2} & \cdots & -s_{k}s_{k} + s_{k} \end{bmatrix}\]参考:
https://mp.weixin.qq.com/s/2xYgaeLlmmUfxiHCbCa8dQ
softmax函数计算时候为什么要减去一个最大值?
http://shuokay.com/2016/07/20/softmax-loss/
Softmax输出及其反向传播推导
https://blog.csdn.net/oBrightLamp/article/details/83959185
softmax函数详解及误差反向传播的梯度求导。这哥们的blog专讲各种op的反向传播。
https://mp.weixin.qq.com/s/HTIgKm8HuZZ_-lIQ3nIFhQ
浅入深出之大话SoftMax
https://mp.weixin.qq.com/s/XBK7T1P7z3rm3o-3BDNeOA
三分钟带你对Softmax划重点
https://mp.weixin.qq.com/s/vhvXsSsEHPVjJGqtCOOwLw
Softmax和交叉熵的深度解析和Python实现
https://mp.weixin.qq.com/s/rw-7-4_07TJ48Mq__HnYEg
用Mixtape代替softmax,CMU提出新方法兼顾表达性和高效性
https://zhuanlan.zhihu.com/p/97475133
从Softmax到AMSoftmax
https://mp.weixin.qq.com/s/fcCS4qDKdGBSKnA_SaYmZA
你不知道的Softmax
https://www.cnblogs.com/geekfx/p/14192158.html
关于Softmax回归的反向传播求导数过程
Softmax loss
通常我们使用的Softmax loss,实际上是由softmax和交叉熵(cross-entropy loss)loss组合而成,所以全称是softmax with cross-entropy loss。
\[l(y,z)=-\sum_{k=0}^C y_k\log (f(z_k))\] \[f(z_k)=e^{z_k}/(\sum_j e^{z_j})\]原始的softmax loss非常优雅,简洁,被广泛用于分类问题。它的特点就是优化类间的距离非常棒,但是优化类内距离时比较弱。
信息论视角:Softmax就是最小化在估计分类概率和“真实”分布之间的交叉熵。
概率论解释:最大似然估计(MLE)。
其实,softmax干的根本就不是max干的活,它并不是找出一个向量中的最大值。它反而和向量版的argmax的作用比较像。
\[\mathrm{argmax} ([2,1,0.1])=[1,0,0]\] \[\mathrm{softmax} ([2,1,0.1])=[0.7,0.2,0.1]\]由于softmax不像argmax这样只选择唯一的一个,也就是所谓的one-hot ,因此得了soft的名字。
softmax分类器对于分数是永远不会满意的:正确分类总能得到更高的可能性,错误分类总能得到更低的可能性,损失值总是能够更小。
但SVM只要边界值被满足了就满意了,不会超过限制去细微地操作具体分数。
参考:
https://www.zhihu.com/question/294679135
softmax和cross-entropy是什么关系?
https://mp.weixin.qq.com/s/lEBbuyPJsUx49BzMaSVhHw
Softmax与交叉熵的数学意义
logits
logits本意是指一个事件发生与该事件不发生的比值的对数。假设一个事件发生的概率为 p,那么该事件的logits为:
\[\text{logits}(p) = \log\frac{p}{1-p}\]但是在tensorflow中:
logits = tf.matmul(X, W) + bias
Y_pred = tf.nn.softmax(logits,name='Y_pred')
可见这里的logits是未进入softmax的概率,也就是未归一化的概率,或者说是softmax的输入。
参考:
https://www.zhihu.com/question/60751553
如何理解深度学习源码里经常出现的logits?
Weighted softmax loss
假如有一个二分类问题,两类的样本数目差距非常之大。比如图像任务中的边缘检测问题,它可以看作是一个逐像素的分类问题。此时两类的样本数目差距非常之大,明显边缘像素的重要性是比非边缘像素大的,此时可以针对性的对样本进行加权。
\[l(y,z)=-\sum_{k=0}^C w_ky_k\log (f(z_k))\]Triplet Loss
Triplet loss通常是在个体级别的细粒度识别上使用,传统的分类是花鸟狗的大类别的识别,但是有些需求是要精确到个体级别,比如精确到哪个人的人脸识别,所以triplet loss的最主要应用也就是face identification,person re-identification,vehicle re-identification的各种identification识别问题上。
当然你可以把每个人当做一个类别来进行分类训练,但是往往最后会造成softmax的维数远大于feature的维数。
论文:
《Deep feature learning with relative distance comparison for person re-identification》
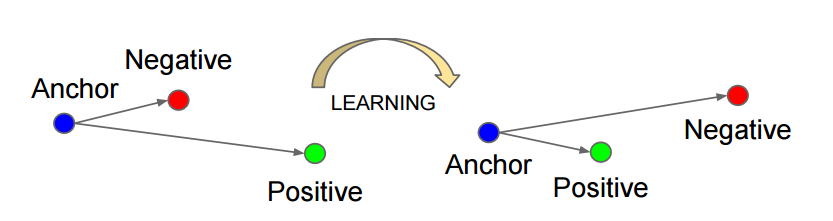
如上图所示,triplet是一个三元组,这个三元组是这样构成的:从训练数据集中随机选一个样本,该样本称为Anchor,然后再随机选取一个和Anchor(记为\(x^a\))属于同一类的样本和不同类的样本,这两个样本对应的称为Positive(记为\(x^p\))和Negative(记为\(x^n\)),由此构成一个(Anchor,Positive,Negative)三元组。

您的打赏,是对我的鼓励
