ML » 机器学习(十七)——主成分分析
2017-01-12 :: 5445 WordsEMD(续)
Gaspard Monge, Comte de Péluse,1746~1818,法国数学家。微分几何之父,巴黎综合理工大学(École Polytechnique)创始人、校长。海军部长。
革命形势在1794年已经开始恶化,蒙日的好友、化学家拉瓦锡就是在那时被声称“革命不需要科学”的群众,送上了断头台。 两年后的现在,50岁的蒙日又被革命群众认定为“不够激进”。他不得不从巴黎逃离,路途中还担心自己的安危——狂热的革命群众随时可能把他抓回去,并送上断头台。
一封意外的来信打消了蒙日的恐惧。写信人是法兰西共和国意大利方面军总司令拿破仑,27岁的总司令在信中表示,除了乐意向蒙日“伸出感激和友谊之手”,还想向他致谢。原来在4年前,他们见过面。当时蒙日担任法国海军部长,拿破仑尚是“不得宠的年轻炮兵军官”。在部长那里,拿破仑受到了“热诚的欢迎”。尽管蒙日根本记不起这件事,拿破仑则依旧“珍藏着这段记忆”。
EMD可以是多维分布之间的距离。一维的EMD也被称为Match distance。
EMD有时也称作Wasserstein距离。
Leonid Vaseršteĭn,俄罗斯数学家,Moscow State University硕博,现居美国,Penn State University教授。Wasserstein是他名字的德文拼法,并为英文文献所沿用。他在去美国之前,曾在德国住过一段时间。
由于最优传输问题的计算比较复杂,因此在DL时代,我们通常使用神经网络来计算EMD距离,例如WGAN。
在文本处理中,有一个和EMD类似的编辑距离(Edit distance),也叫做Levenshtein distance。它是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。一般来说,编辑距离越小,两个串的相似度越大。
严格来说,Edit distance是一系列字符串相似距离的统称。除了Levenshtein distance之外,还包括Hamming distance等。
Vladimir Levenshtein,1935年生,俄罗斯数学家,毕业于莫斯科州立大学。2006年获得IEEE Richard W. Hamming Medal。
参考:
https://vincentherrmann.github.io/blog/wasserstein/
Wasserstein GAN and the Kantorovich-Rubinstein Duality
http://chaofan.io/archives/earth-movers-distance-%e6%8e%a8%e5%9c%9f%e6%9c%ba%e8%b7%9d%e7%a6%bb
Earth Mover’s Distance——推土机距离
https://mp.weixin.qq.com/s/rvPLYa1NFg_LRvb8Y8-aCQ
Wasserstein距离在生成模型中的应用
https://mp.weixin.qq.com/s/2xOrSyyWSbp8rBVbFoNrxQ
Wasserstein is all you need:构建无监督表示的统一框架
https://mp.weixin.qq.com/s/g4F50zLNs_aC1WUuCMNdXg
一文详解Wasserstein距离
https://mp.weixin.qq.com/s/NXDJ4uCpdX-YcWiKAsjJLQ
传说中的推土机距离基础,最优传输理论了解一下
https://mp.weixin.qq.com/s/5sNXmQbINIWMGjX5TYAPYw
最优传输理论你理解了,传说中的推土机距离重新了解一下
https://mp.weixin.qq.com/s/iwZrWYbppwStJlXESUufZQ
想要算一算Wasserstein距离?这里有一份PyTorch实战
https://mp.weixin.qq.com/s/itQNrNsdjAgPl5R48V-HtQ
计算最优传输(Computational Optimal Transport)
https://zhuanlan.zhihu.com/p/72803739
Word Mover’s Distance-文档距离优化方案
https://mp.weixin.qq.com/s/Zi9v_sbxPkHWUWwNhMMMAg
编辑距离
https://zhuanlan.zhihu.com/p/270675634
点云距离度量:完全解析EMD距离(Earth Mover’s Distance)
https://zhuanlan.zhihu.com/p/358895758
统计距离(STATISTICAL DISTANCE)
主成分分析
真实的训练数据总是存在各种各样的问题。
比如拿到一个汽车的样本,里面既有以“千米/每小时”度量的最大速度特征,也有“英里/小时”的最大速度特征。显然这两个特征有一个是多余的,我们需要找到,并去除这个冗余。
再比如,针对飞行员的调查,包含两个特征:飞行的技能水平和对飞行的爱好程度。由于飞行员是很难培训的,因此如果没有对飞行的热爱,也就很难学好飞行。所以这两个特征实际上是强相关的(strongly correlated)。如下图所示:
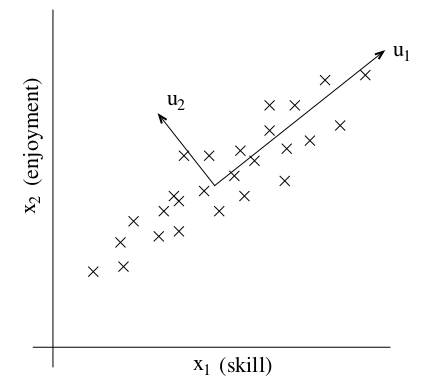
我们的目标就是找出上图中所示的向量\(u_1\)。
为了实现这两个目标,我们可以采用PCA(Principal components analysis)算法。
数据的规则化处理
在进行PCA算法之前,我们首先要对数据进行预处理,使之规则化。其方法如下:
1.\(\mu=\frac{1}{m}\sum_{i=1}^mx^{(i)}\)
2.\(x^{(i)}:=x^{(i)}-\mu\)
3.\(\sigma_j^2=\frac{1}{m}\sum_i(x^{(i)})^2\)
4.\(x_j^{(i)}:=x_j^{(i)}/\sigma_j\)
多数情况下,特征空间中,不同特征向量所代表的维度之间,并不能直接比较。
比如,摄氏度和华氏度,虽然都是温度的单位,但两种温标的原点和尺度都不相同,因此需要规范化之后才能比较。
步骤1和2,用于消除原点偏差(常数项偏差)。步骤3和4,用于统一尺度(一次项偏差)。
虽然上面的办法,对于二次以上的偏差无能为力,然而多数情况下,这种处理,已经比原始状态好多了。
PCA算法推导
回到之前的话题,为了找到主要的方向u,我们首先观察一下,样本点在u上的投影应该是什么样子的。
 |
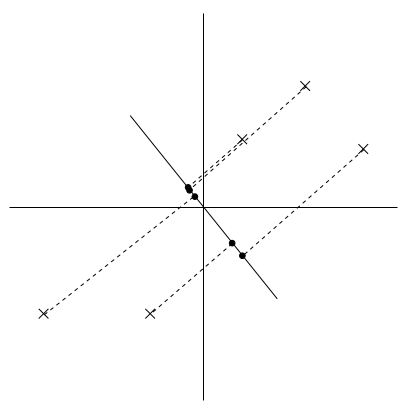 |
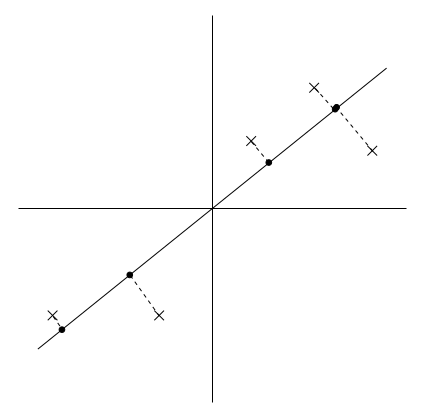
上图所示是5个样本在不同向量上的投影情况。其中,X表示样本点,而黑点表示样本在u上的投影。
很显然,左图中的u就是我们需要求解的主成分的方向。和右图相比,左图中各样本点x在u上的投影点比较分散,也就是投影点之间的方差较大。
由《机器学习(十二)》的公式1,可知样本点x在单位向量u上的投影为:\(x^Tu\)。
因此,这个问题的代价函数为:
\[\begin{align} &\frac{1}{m}\sum_{i=1}^m\left(x^{(i)^T}u\right)^2=\frac{1}{m}\sum_{i=1}^m\left(x^{(i)^T}u\right)^T\left(x^{(i)^T}u\right) \\&=\frac{1}{m}\sum_{i=1}^mu^Tx^{(i)}x^{(i)^T}u=u^T\left(\frac{1}{m}\sum_{i=1}^mx^{(i)}x^{(i)^T}\right)u=u^T\Sigma u \end{align}\]即:
\[\begin{align} &\operatorname{max}_{u}& & u^T\Sigma u\\ &\operatorname{s.t.}& & u^Tu=1 \end{align}\]其中的矩阵\(\Sigma\)实际上是一个对角阵,对角线元素\(\sigma_{ii}\)表示x的第i维的方差。
其拉格朗日函数为:
\[\mathcal{L}(u)=u^T\Sigma u-\lambda(u^Tu-1)\]对u求导可得:
\[\nabla_u\mathcal{L}(u)=\Sigma u-\lambda u\]这里的矩阵求导步骤,参见《机器学习(十一)》中的公式5.12的推导过程。
令导数为0可得,当\(\lambda\)为\(\Sigma\)的特征值的时候,该代价函数得到最优解。
这里的推导过程,求解的是1维的PCA,但结论对于k维的PCA也是成立的。
一个n阶矩阵有n个特征值,这些特征值可按绝对值大小排序,绝对值越大的,越重要。其中最大的k个特征值,被称作k principal components,这就是主成分分析(Principal components analysis,PCA)算法的命名来历。
我们以最大的k个特征值所对应的特征向量,构建样本空间Y:
\[y^{(i)}=\begin{bmatrix} u_1^Tx^{(i)}\\ u_2^Tx^{(i)}\\ \cdots \\ u_k^Tx^{(i)} \end{bmatrix}\in R^k\tag{1}\]可以看出PCA算法实际上是个降维(dimensionality reduction)算法。
PCA相关系数的推导
\(\rho(y_k,x_i)\)表示第k个主成分与第i个变量的相关系数,也被称为因子负荷或主成分负荷。
推导:
相关系数的定义为:
\[\rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}\]由特征值的定义可得:
\[u_i^T\Sigma u_i=u_i^T\lambda_i u_i=\lambda_iu_i^Tu_i\]因为u是单位正交阵,所以:
\[u_i^T\Sigma u_i=\lambda_i\] \[Var(y_k)=Var(u_k^Tx)=(u_k^Tx)(u_k^Tx)^T=u_k^Txx^Tu_k=u_k^T\Sigma u_k=\lambda_k\]令\(x=Ay\),则:
\[Cov(y_k,x_i)=Cov(y_k,a_{ik}y_k)=a_{ik}Cov(y_k,y_k)=a_{ik}Var(y_k)=a_{ik}\lambda_k\] \[Var(x_i)=\sigma_{ii}\]综上可得:
\[\rho(y_k,x_i)=\frac{a_{ik}\lambda_k}{\sqrt{\lambda_k}\sqrt{\sigma_{ii}}}=\frac{a_{ik}\sqrt{\lambda_k}}{\sqrt{\sigma_{ii}}}\]PCA的用途
为了便于理解PCA算法,我们以如下图片的处理过程为例,进行说明。

第一排从左往右依次为:原图(450*333)、k=1、k=5;第二排从左往右依次为:k=20、k=50。
从中可以看出,k=50时,图像的效果已经和原图相差无几。而原图是个450*333的高阶矩阵。
在图像处理领域,奇异值不仅可以应用在数据压缩上,还可以对图像去噪。如果一副图像包含噪声,我们有理由相信那些较小的奇异值就是由于噪声引起的。当我们强行令这些较小的奇异值为0时,就可以去除图片中的噪声。
PCA的一个很大的优点是,它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
PCA和ALS的联系与区别
令:
\[Y_{k\times m}=\begin{bmatrix}y^{(1)} & \cdots & y^{(m)}\end{bmatrix}\]则由公式1可得:
\[Y_{k\times m}=U_{n\times k}^TX_{n\times m}\]变换可得:
\[X_{n\times m}\approx U_{n\times k}Y_{k\times m}\]由于PCA是个降维算法,因此这个变换实际上也是个近似变换。
从上面可以看出,PCA和ALS实际上都是矩阵的降维分解算法。它们的差别在于:
1.PCA的U矩阵是单位正交矩阵,而ALS的分解矩阵则没有这个限制。
2.ALS从原理上虽然也是矩阵的奇异值或特征值的应用,然而其求解过程,却并不涉及矩阵的奇异值或特征值的运算,因此运算效率非常高。
3.ALS是个迭代算法,容易掉入局部最优陷阱中。
PCA和特征选择的区别
两者虽然都是降维算法,但特征选择是在原有的n个特征中选择k个特征,而PCA是重建k个新的特征。

您的打赏,是对我的鼓励
