ML » 机器学习(十一)——高斯混合模型和EM算法
2016-09-08 :: 7863 Words高斯混合模型和EM算法
GMM与概率分布(续)
Andrew讲义在介绍GMM的时候,由于要和K-means做对比,因此主要介绍了GMM在聚类中的应用,但GMM的应用并不仅于此。
我们知道函数有泰勒级数和傅立叶级数等展开方式,同样的任意随机变量的概率分布,也可以展开为若干高斯分布的和:
\[p(x)=\sum_{m=1}^M c_m \mathcal{N}(x;\mu_m,\sigma_m^2)\]不难看出上式和上节的公式5是等价的。
GMM的这种用法在语音识别领域用的较多,是GMM-HMM算法的核心思想之一。
参考
http://cseweb.ucsd.edu/~atsmith/project1_253.pdf
Clustering With EM and K-Means
https://mp.weixin.qq.com/s/wk3_wG1xSuMX1HjJeEgErQ
kmeans聚类理论篇K的选择(轮廓系数)
https://mp.weixin.qq.com/s/tLcF7_jjl3_FmjM7L1kcfw
一文详解高斯混合模型原理
https://mp.weixin.qq.com/s/RpEgTMRUM4GWhIdIPvkGTg
优于VAE,为万能近似器高斯混合模型加入Wasserstein距离
https://zhuanlan.zhihu.com/p/85338773
高斯混合模型(GMM)推导及实现
https://mp.weixin.qq.com/s/Uayd-KiXeoL5vBUyC1-oDQ
小孩都看得懂的GMM
EM算法
本节将进一步讨论EM算法的性质,并将之应用到使用latent random variables的一大类估计问题中。
Jensen不等式
首先我们给出凸函数的定义:
设f是定义域为实数的函数,如果对于所有的实数x,\(f''(x)\ge 0\),那么f是凸函数。当x是向量时,如果其Hessian矩阵H是半正定的(\(H\ge 0\)),那么f是凸函数。如果\(f''(x)>0\)或\(H>0\),那么称f是严格凸函数。
Jensen不等式表述如下:
如果f是凸函数,X是随机变量,那么\(E[f(X)]\ge f(EX)\)。
特别地,如果f是严格凸函数,那么\(E[f(X)]=f(EX)\),当且仅当\(p(X=EX)=1\)。也就是说X是常量。
在不引起误会的情况下,\(E[X]\)简写做\(EX\)。
这个不等式的含义如下图所示:
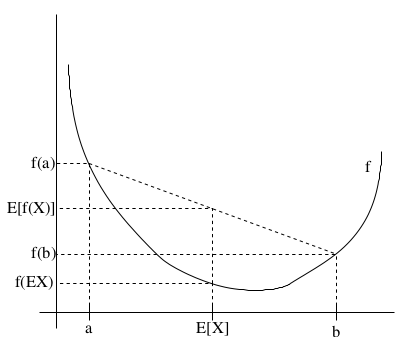
Jensen不等式应用于凹函数时,不等号方向反向,也就是\(E[f(X)]\le f(EX)\)
Johan Ludwig William Valdemar Jensen,1859~1925,丹麦人。主业工程师,副业数学家。
EM算法的一般形式
EM算法一般形式的似然函数为:
\[\ell(\theta)=\sum_{i=1}^m\log p(x^{(i)};\theta)=\sum_{i=1}^m\log \sum_zp(x^{(i)},z^{(i)};\theta)\tag{1}\]根据这个公式直接求\(\theta\)一般比较困难,但是如果确定了z之后,求解就容易了。
EM算法是一种解决存在隐含变量优化问题的有效方法。既然不能直接最大化\(\ell(\theta)\),我们可以不断地建立\(\ell(\theta)\)的下界(E-Step),然后优化下界(M-Step)。
这里首先假设\(z^{(i)}\)的分布为\(Q_i\)。显然:
\[\sum_zQ_i(z)=1,Q_i(z)\ge 0\] \[\begin{align} \ell(\theta)&=\sum_{i=1}^m\log \sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta) \\&=\sum_{i=1}^m\log \sum_{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \\&\ge\sum_{i=1}^m\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\tag{2} \end{align}\]这里解释一下最后一步的不等式变换。
首先,根据数学期望的定义公式:
\[E[X]=\sum_{i=1}^nx_ip_i\]可知:
\[\sum_{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=E\left[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\right]\]又因为\(f(x)=\log x\)是凹函数,根据Jensen不等式可得:
\[f\left(E_{z^{(i)}\sim Q_i}\left[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\right]\right)\ge E_{z^{(i)}\sim Q_i}\left[f\left(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\right)\right]\]综上,公式2给出了\(\ell(\theta)\)的下界。对于\(Q_i\)的选择,有多种可能,那种更好的?
假设\(\theta\)已经给定,那么\(\ell(\theta)\)的值就取决于\(Q_i(z^{(i)})\)和\(p(x^{(i)},z^{(i)})\)了。我们可以通过调整这两个概率,使下界不断上升,以逼近\(\ell(\theta)\)的真实值。当不等式变成等式时,下界达到最大值。
由Jensen不等式相等的条件可知,\(\ell(\theta)\)的下界达到最大值的条件为:
\[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=c\]其中c为常数。
这实际上表明:
\[Q_i(z^{(i)})\propto p(x^{(i)},z^{(i)};\theta)\]其中的\(\propto\)符号是两者成正比例的意思。
从中还可以推导出:
\[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=c=\frac{\sum_zp(x^{(i)},z^{(i)};\theta)}{\sum_zQ_i(z^{(i)})}\]因为\(\sum_zQ_i(z^{(i)})=1\),所以上式可变形为:
\[Q_i(z^{(i)})=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum_zp(x^{(i)},z^{(i)};\theta)}=\frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)}=p(z^{(i)}\mid x^{(i)};\theta)\]可见,当\(Q_i(z^{(i)})\)为\(z^{(i)}\)的后验分布时,\(\ell(\theta)\)的下界达到最大值。
因此,EM算法的过程为:
Repeat until convergence {
(E-step) For each i:
\[Q_i(z^{(i)}):=p(z^{(i)}\mid x^{(i)};\theta)\](M-step) Update the parameters:
\[\theta:=\arg\max_\theta\sum_i\sum_zQ_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\]}
如何保证算法的收敛性呢?
如果我们用\(\theta^{(t)}\)和\(\theta^{(t+1)}\)表示EM算法第t次和第t+1次迭代后的结果,那么我们的任务就是证明\(\ell(\theta^{(t)})\le \ell(\theta^{(t+1)})\)。
由公式1和2可得:
\[\ell(\theta)\ge\sum_i\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\tag{3}\]由之前的讨论可以看出,E-Step中的步骤是使上式的等号成立的条件,即:
\[\ell(\theta^{(t)})=\sum_i\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}\]因为公式3对于任意\(Q_i\)和\(\theta\)都成立,因此:
\[\ell(\theta^{(t+1)})\ge\sum_i\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})}\]因为M-Step的最大化过程,可得:
\[\sum_i\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})}\ge\sum_i\sum_{z^{(i)}}Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}\]综上可得:\(\ell(\theta^{(t)})\le \ell(\theta^{(t+1)})\)
事实上,如果我们定义:
\[J(Q,\theta)=\sum_i\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\]则EM算法可以看作是J函数的坐标上升法。E-Step固定\(\theta\),优化Q;M-Step固定Q,优化\(\theta\)。
参考:
https://mp.weixin.qq.com/s/NbM4sY93kaG5qshzgZzZIQ
EM算法的九层境界:Hinton和Jordan理解的EM算法
https://mp.weixin.qq.com/s/FSID_FLMVxrKEj_padg_bQ
EM算法是炼金术吗?
https://mp.weixin.qq.com/s/JSnPTVRgXO3aih5srU1eZQ
EM算法原理总结
https://mp.weixin.qq.com/s/192sLXAvLKzwsTKCZs-AuA
一文详尽系列之EM算法
https://mp.weixin.qq.com/s/D2Am1tyCt3DQLvF0ylLJrg
深入浅出聚类算法!如何对王者英雄聚类分析,探索英雄之间的秘密
https://mp.weixin.qq.com/s/PKfsSMMtwks_KqRkpKJbKA
理解高斯混合模型中期望最大化的M-Step
重新审视混合高斯模型
下面给出混合高斯模型各参数的推导过程。
E-Step很简单:
\[w_j^{(i)}=Q_i(z^{(i)}=j)=p(z^{(i)}=j\mid x^{(i)};\phi,\mu,\Sigma)\]在M-Step中,我们将各个变量和分布的概率密度函数代入,可得:
\[\begin{align} &\sum_{i=1}^m\sum_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \\&=\sum_{i=1}^m\sum_{j=1}^kQ_i(z^{(i)}=j)\log\frac{p(x^{(i)}\mid z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{Q_i(z^{(i)}=j)} \\&=\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\log\frac{\frac{1}{(2\pi)^{n/2}\lvert\Sigma_j\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j)\right)\cdot \phi_j}{w_j^{(i)}} \end{align}\]对\(\mu_l\)求导,可得:
\[\begin{align} &\nabla_{\mu_l}\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\log\frac{\frac{1}{(2\pi)^{n/2}\lvert\Sigma_j\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j)\right)\cdot \phi_j}{w_j^{(i)}} \\&=-\nabla_{\mu_l}\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\frac{1}{2}(x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j) \\&=\frac{1}{2}\sum_{i=1}^mw_l^{(i)}\nabla_{\mu_l}(2\mu_l^T\Sigma_l^{-1}x^{(i)}-\mu_l^T\Sigma_l^{-1}\mu_l)=\sum_{i=1}^mw_l^{(i)}(\Sigma_l^{-1}x^{(i)}-\Sigma_l^{-1}\mu_l)\tag{4} \end{align}\]这里对最后一步的推导,做一个说明。为了便于以下的讨论,我们引入符号“tr”,该符号表示矩阵的主对角线元素之和,也被叫做矩阵的“迹”(Trace)。按照通常的写法,在不至于误会的情况下,tr后面的括号会被省略。
tr的其他性质还包括:
\[\operatorname{tr}\,a=a,a\in R\tag{5.1}\] \[\operatorname{tr}(A + B) = \operatorname{tr}(A) + \operatorname{tr}(B)\tag{5.2}\] \[\operatorname{tr}(cA) = c \operatorname{tr}(A)\tag{5.3}\] \[\operatorname{tr}(A) = \operatorname{tr}(A^{\mathrm T})\tag{5.4}\] \[\operatorname{tr}(AB) = \operatorname{tr}(BA)\tag{5.5}\] \[\operatorname{tr}(ABCD) = \operatorname{tr}(BCDA) = \operatorname{tr}(CDAB) = \operatorname{tr}(DABC)\tag{5.6}\] \[\nabla_A\operatorname{tr}(AB)=B^T\tag{5.7}\] \[\nabla_{A^T}f(A)=(\nabla_Af(A))^T\tag{5.8}\] \[\nabla_A\operatorname{tr}(ABA^TC)=CAB+C^TAB^T\tag{5.9}\] \[\nabla_{A^T}\operatorname{tr}(ABA^TC)=B^TA^TC^T+BA^TC\tag{5.10}\] \[\nabla_A\mid A\mid =\mid A\mid (A^{-1})^T\tag{5.11}\]因为\(\mu_l^T\Sigma_l^{-1}\mu_l\)是实数,由公式5.1可得:
\[\nabla_{\mu_l}\mu_l^T\Sigma_l^{-1}\mu_l=\nabla_{\mu_l}\operatorname{tr}(\mu_l^T\Sigma_l^{-1}\mu_l)\]由公式5.10可得:
\[\nabla_{\mu_l}\operatorname{tr}(\mu_l^T\Sigma_l^{-1}\mu_l)=(\Sigma_l^{-1})^T(\mu_l^T)^TI^T+\Sigma_l^{-1}(\mu_l^T)^TI=(\Sigma_l^{-1})^T\mu_l+\Sigma_l^{-1}\mu_l\]因为\(\Sigma_l^{-1}\)是对称矩阵,因此,综上可得:
\[\nabla_{\mu_l}\mu_l^T\Sigma_l^{-1}\mu_l=2\Sigma_l^{-1}\mu_l\tag{5.12}\]回到正题,令公式4等于0,可得:
\[\mu_j:=\frac{\sum_{i=1}^mw_j^{(i)}x^{(i)}}{\sum_{i=1}^mw_j^{(i)}}\]同样的,对\(\phi_j\)求导,可得:
\[\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\log\phi_j\]因为存在\(\sum_{j=1}^k\phi_j=1\)这样的约束,因此需要使用拉格朗日函数:
\[\mathcal{L}(\phi)=\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}\log\phi_j+\beta(\sum_{j=1}^k\phi_j-1)\]这里的\(\beta\)是拉格朗日乘子,\(\phi_j\ge 0\)的约束条件不用考虑,因为对\(\log\phi_j\)求导已经隐含了这个条件。
因此:
\[\frac{\partial\mathcal{L}(\phi)}{\partial\phi_j}=\sum_{i=1}^m\frac{w_j^{(i)}}{\phi_j}+\beta\]令上式等于0,可得:
\[\frac{\sum_{i=1}^mw_j^{(i)}}{\phi_j}=-\beta=\frac{\sum_{i=1}^m\sum_{j=1}^kw_j^{(i)}}{\sum_{j=1}^k\phi_j}\]因为\(\sum_{j=1}^k\phi_j=1,\sum_{j=1}^kw_j^{(i)}=1\),所以:
\[-\beta=\frac{\sum_{i=1}^m1}{1}=m\]因此:
\[\phi_j:=\frac{1}{m}\sum_{i=1}^mw_j^{(i)}\]
您的打赏,是对我的鼓励
