ML » 机器学习(十四)——协同过滤的ALS算法(2)
2016-09-28 :: 5971 Words协同过滤的ALS算法(续)
Kendall秩相关系数(Kendall rank correlation coefficient)
对于秩变量对\((x_i,y_i),(x_j,y_j)\):
\[(x_i-x_j)(y_i-y_j)\begin{cases} >0, & \text{concordant} \\ =0, & \text{neither concordant nor discordant} \\ <0, & \text{discordant} \\ \end{cases}\] \[\tau = \frac{(\text{number of concordant pairs}) - (\text{number of discordant pairs})}{n (n-1) /2}\]Sir Maurice George Kendall,1907~1983,英国统计学家。这个人职业生涯的大部分时间都是一个公务员,二战期间出任英国船运协会副总经理。1949年以后担任伦敦大学教授。
参见:
https://en.wikipedia.org/wiki/Kendall_rank_correlation_coefficient
Tanimoto系数
\[T(x,y)=\frac{\mid X\cap Y\mid }{\mid X\cup Y\mid }=\frac{\mid X\cap Y\mid }{\mid X\mid +\mid Y\mid -\mid X\cap Y\mid }=\frac{\sum x_iy_i}{\sqrt{\sum x_i^2}+\sqrt{\sum y_i^2}-\sum x_iy_i}\]该系数由Taffee T. Tanimoto于1960年提出。Tanimoto生平不详,从名字来看,应该是个日本人。在其他领域,它还有另一个名字Jaccard similarity coefficient。(两者的系数公式一致,但距离公式略有差异。)
如果向量的每个维度取值是二值(0或1),那么Tanimoto系数就等同Jaccard距离。
Paul Jaccard,1868~1944,苏黎世联邦理工学院(ETH Zurich)博士,苏黎世联邦理工学院植物学教授。ETH Zurich可是出了24个诺贝尔奖得主的。
参见:
https://en.wikipedia.org/wiki/Jaccard_index
https://www.cnblogs.com/daniel-D/p/3244718.html
漫谈:机器学习中距离和相似性度量方法
https://mp.weixin.qq.com/s/rrIdxEEwFJMWbvbhn_DYDw
协同过滤算法分布式实现
https://zhuanlan.zhihu.com/p/138107999
常见的距离算法和相似度计算方法
https://mp.weixin.qq.com/s/OpBKbF1UHEAuosXjNDKqOA
机器学习距离与相似度计算
https://mp.weixin.qq.com/s/cYfbZtFFd9jvnN4p8T20UQ
9个数据科学中常见距离度量总结以及优缺点概述
ALS算法原理
http://www.cnblogs.com/luchen927/archive/2012/02/01/2325360.html
机器学习相关——协同过滤
https://mp.weixin.qq.com/s/Xgg61ICqkUo9ovdEV7G8Cw
推荐算法综述
https://mp.weixin.qq.com/s/lBj0Z9vY9FcEFQnk0VrdOw
协同过滤推荐算法
上面的网页概括了ALS算法出现之前的协同过滤算法的概况。
ALS算法是2008年以来,用的比较多的协同过滤算法。它已经集成到Spark的Mllib库中,使用起来比较方便。
从协同过滤的分类来说,ALS算法属于User-Item CF,也叫做混合CF。它同时考虑了User和Item两个方面。
用户和商品的关系,可以抽象为如下的三元组:<User,Item,Rating>。其中,Rating是用户对商品的评分,表征用户对该商品的喜好程度。
假设我们有一批用户数据,其中包含m个User和n个Item,则我们定义Rating矩阵\(R_{m\times n}\),其中的元素\(r_{ui}\)表示第u个User对第i个Item的评分。
在实际使用中,由于n和m的数量都十分巨大,因此R矩阵的规模很容易就会突破1亿项。这时候,传统的矩阵分解方法对于这么大的数据量已经是很难处理了。
另一方面,一个用户也不可能给所有商品评分,因此,R矩阵注定是个稀疏矩阵。矩阵中所缺失的评分,又叫做missing item。
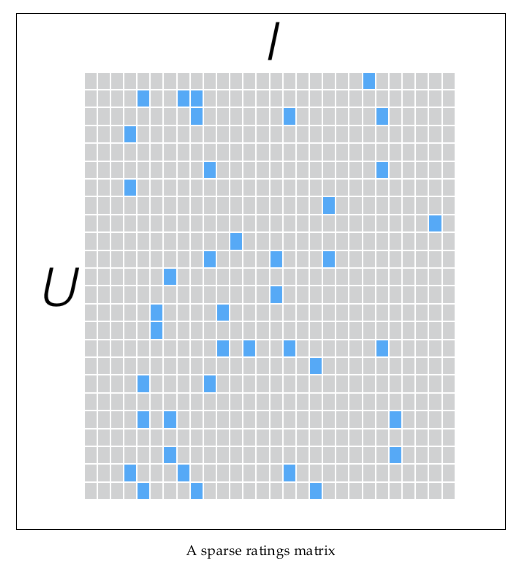
针对这样的特点,我们可以假设用户和商品之间存在若干关联维度(比如用户年龄、性别、受教育程度和商品的外观、价格等),我们只需要将R矩阵投射到这些维度上即可。这个投射的数学表示是:
\[R_{m\times n}\approx X_{m\times k}Y_{n\times k}^T\tag{1}\]这里的\(\approx\)表明这个投射只是一个近似的空间变换。
不懂这个空间变换的同学,可参见《线性代数(二)》中的“奇异值分解”的内容,或是《机器学习(十七)》中的“主成分分析”的内容。
一般情况下,k的值远小于n和m的值,从而达到了数据降维的目的。
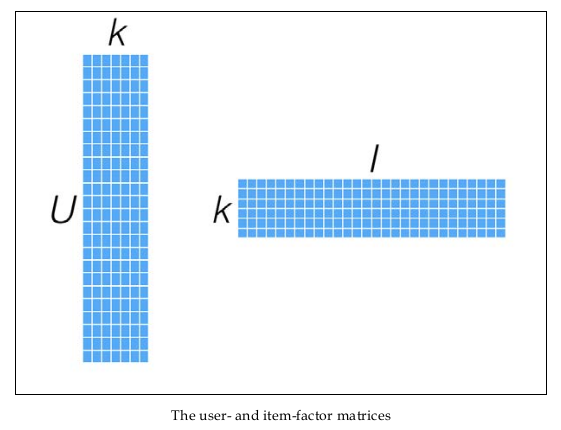
幸运的是,我们并不需要显式的定义这些关联维度,而只需要假定它们存在即可,因此这里的关联维度又被称为Latent factor。k的典型取值一般是20~200。
这种方法被称为概率矩阵分解算法(probabilistic matrix factorization,PMF)。ALS算法是PMF在数值计算方面的应用。
为了使低秩矩阵X和Y尽可能地逼近R,需要最小化下面的平方误差损失函数:
\[\min_{x_*,y_*}\sum_{u,i\text{ is known}}(r_{ui}-x_u^Ty_i)^2\]考虑到矩阵的稳定性问题,使用Tikhonov regularization,则上式变为:
\[\min_{x_*,y_*}L(X,Y)=\min_{x_*,y_*}\sum_{u,i\text{ is known}}(r_{ui}-x_u^Ty_i)^2+\lambda(\mid x_u\mid ^2+\mid y_i\mid ^2)\tag{2}\]优化上式,得到训练结果矩阵\(X_{m\times k},Y_{n\times k}\)。预测时,将User和Item代入\(r_{ui}=x_u^Ty_i\),即可得到相应的评分预测值。
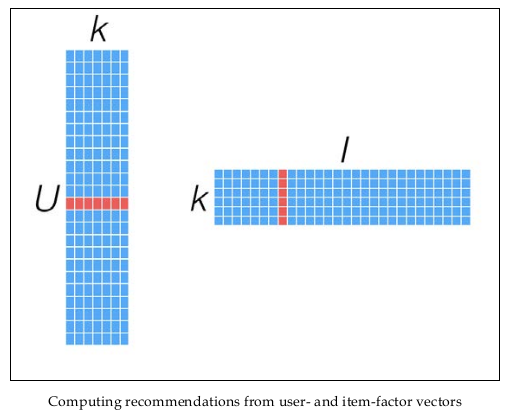
同时,矩阵X和Y,还可以用于比较不同的User(或Item)之间的相似度,如下图所示:
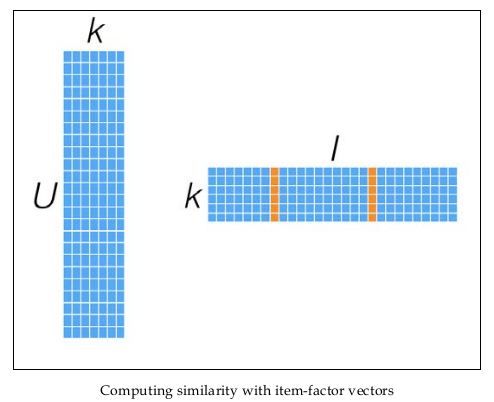
ALS算法的缺点在于:
1.它是一个离线算法。
2.无法准确评估新加入的用户或商品。这个问题也被称为Cold Start问题。
ALS算法优化过程的推导
公式2的直接优化是很困难的,因为X和Y的二元导数并不容易计算,这时可以使用类似坐标下降法的算法,固定其他维度,而只优化其中一个维度。
对\(x_u\)求导,可得:
\[\begin{align} \frac{\partial L}{\partial x_u}&=-2\sum_i(r_{ui}-x_u^Ty_i)y_i+2\lambda x_u \\&=-2\sum_i(r_{ui}-y_i^Tx_u)y_i+2\lambda x_u \\&=-2Y^Tr_u+2Y^TYx_u+2\lambda x_u \end{align}\]令导数为0,可得:
\[Y^TYx_u+\lambda Ix_u=Y^Tr_u\Rightarrow x_u=(Y^TY+\lambda I)^{-1}Y^Tr_u\tag{3}\]同理,对\(y_i\)求导,由于X和Y是对称的,因此可得类似的结论:
\[y_i=(X^TX+\lambda I)^{-1}X^Tr_i\tag{4}\]因此整个优化迭代的过程为:
1.随机生成X、Y。(相当于对迭代算法给出一个初始解。)
Repeat until convergence {2.固定Y,使用公式3更新\(x_u\)。
3.固定X,使用公式4更新\(y_i\)。}
一般使用RMSE(root-mean-square error)评估误差是否收敛,具体到这里就是:
\[RMSE=\sqrt{\frac{\sum(R-XY^T)^2}{N}}\]其中,N为三元组<User,Item,Rating>的个数。当RMSE值变化很小时,就可以认为结果已经收敛。
算法复杂度:
1.求\(x_u\):\(O(k^2N+k^3m)\)
2.求\(y_i\):\(O(k^2N+k^3n)\)
可以看出当k一定的时候,这个算法的复杂度是线性的。
因为这个迭代过程,交替优化X和Y,因此又被称作交替最小二乘算法(Alternating Least Squares,ALS)。
隐式反馈
用户给商品评分是个非常简单粗暴的用户行为。在实际的电商网站中,还有大量的用户行为,同样能够间接反映用户的喜好,比如用户的购买记录、搜索关键字,甚至是鼠标的移动。我们将这些间接用户行为称之为隐式反馈(implicit feedback),以区别于评分这样的显式反馈(explicit feedback)。
隐式反馈有以下几个特点:
1.没有负面反馈(negative feedback)。用户一般会直接忽略不喜欢的商品,而不是给予负面评价。
2.隐式反馈包含大量噪声。比如,电视机在某一时间播放某一节目,然而用户已经睡着了,或者忘了换台。
3.显式反馈表现的是用户的喜好(preference),而隐式反馈表现的是用户的信任(confidence)。比如用户最喜欢的一般是电影,但观看时间最长的却是连续剧。大米购买的比较频繁,量也大,但未必是用户最想吃的食物。
4.隐式反馈非常难以量化。
ALS-WR
针对隐式反馈,有ALS-WR算法(ALS with Weighted-\(\lambda\)-Regularization)。
首先将用户反馈分类:
\[p_{ui}=\begin{cases} 1, & \text{preference} \\ 0, & \text{no preference} \\ \end{cases}\]但是喜好是有程度差异的,因此需要定义程度系数:
\[c_{ui}=1+\alpha r_{ui}\]这里的\(r_{ui}\)表示原始量化值,比如观看电影的时间;
这个公式里的1表示最低信任度,\(\alpha\)表示根据用户行为所增加的信任度。
最终,损失函数变为:
\[\min_{x_*,y_*}L(X,Y)=\min_{x_*,y_*}\sum_{u,i}c_{ui}(p_{ui}-x_u^Ty_i)^2+\lambda(\sum_u\mid x_u\mid ^2+\sum_i\mid y_i\mid ^2)\]除此之外,我们还可以使用指数函数来定义\(c_{ui}\):
\[c_{ui}=1+\alpha \log(1+r_{ui}/\epsilon)\]ALS-WR没有考虑到时序行为的影响,时序行为相关的内容,可参见:
http://www.jos.org.cn/1000-9825/4478.htm
基于时序行为的协同过滤推荐算法
参考
参考论文:
《Large-scale Parallel Collaborative Filtering forthe Netflix Prize》
《Collaborative Filtering for Implicit Feedback Datasets》
《Matrix Factorization Techniques for Recommender Systems》
其他参考:
http://www.jos.org.cn/html/2014/9/4648.htm
基于大规模隐式反馈的个性化推荐
http://www.fuqingchuan.com/2015/03/812.html
协同过滤之ALS-WR算法
http://www.docin.com/p-714582034.html
基于矩阵分解的协同过滤算法
http://www.tuicool.com/articles/fANvieZ
Spark MLlib中的协同过滤
http://www.68idc.cn/help/buildlang/ask/20150727462819.html
Alternating Least Squares(ASL)的数学推导
https://mp.weixin.qq.com/s/bRhIm8Xvlb51zE2HpDO5Og
一文读懂推荐系统知识体系
http://mp.weixin.qq.com/s/QhP3wRGbrO7sYSDNm8z0gQ
常用推荐算法(50页干货)
https://zhuanlan.zhihu.com/p/23036112
推荐系统常用的推荐算法
https://mp.weixin.qq.com/s/6x8cK_SDW67At3IUZ15ijQ
协同过滤典型算法概述
https://mp.weixin.qq.com/s/wtvwWZhqCRjJgdCpa7qdJw
矩阵分解在协同过滤推荐中的应用
https://mp.weixin.qq.com/s/sUQPaiYAfRpCFryrHMqPoA
想写出人见人爱的推荐系统,先了解经典矩阵分解技术
https://mp.weixin.qq.com/s/7C_XRgPFh41r05SZdA2NfA
推荐系统之矩阵分解模型:科普篇
https://mp.weixin.qq.com/s/Fy2ZyxYvRj3C8BqOp6IGPQ
推荐系统之矩阵分解模型:原理篇
https://mp.weixin.qq.com/s/NnykbxFA6xnTUbLzX8GVIg
推荐系统之矩阵分解模型:实践篇

您的打赏,是对我的鼓励
