• 因子分析模型（续）
• 因子分析的EM估计
• 协同过滤的ALS算法
  • 协同过滤概述
    • 欧氏距离
    • Cosine相似度
    • 皮尔逊相关系数（Pearson product-moment correlation coefficient，PPMCC or PCC）：
    • Spearman秩相关系数（Spearman’s rank correlation coefficient）

因子分析模型（续）

把这些结果合在一起，可得：

\[\begin{bmatrix} z \\ x \end{bmatrix}\sim N\left(\begin{bmatrix} \vec{0} \\ \mu \end{bmatrix},\begin{bmatrix} I & \Lambda^T \\ \Lambda & \Lambda \Lambda^T+\Psi \end{bmatrix}\right)\tag{1}\]

从这个结论可以看出：\(x\sim N(\mu,\Lambda \Lambda^T+\Psi)\)

因此它的对数似然函数为：

\[\ell(\mu,\Lambda,\Psi)=\log\prod_{i=1}^m\frac{1}{(2\pi)^{n/2}\lvert\Lambda \Lambda^T+\Psi\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu)^T(\Lambda \Lambda^T+\Psi)^{-1}(x^{(i)}-\mu)\right)\]

但这个函数是很难最大化的，需要使用EM算法解决之。

因子分析的EM估计

E-step比较简单。由《机器学习（十）》公式1、2和公式1，可得：

\[\mu_{z^{(i)}\mid x^{(i)}}=\Lambda^T(\Lambda \Lambda^T+\Psi)^{-1}(x^{(i)}-\mu)\] \[\Sigma_{z^{(i)}\mid x^{(i)}}=I-\Lambda^T(\Lambda \Lambda^T+\Psi)^{-1}\Lambda\]

因此：

\[Q_i(z^{(i)})=\frac{1}{(2\pi)^{n/2}\lvert\Sigma_{z^{(i)}\mid x^{(i)}}\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu_{z^{(i)}\mid x^{(i)}})^T\Sigma_{z^{(i)}\mid x^{(i)}}^{-1}(x^{(i)}-\mu_{z^{(i)}\mid x^{(i)}})\right)\]

M-step的最大化的目标是：

\[\sum_{i=1}^m\int_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\mu,\Lambda,\Psi)}{Q_i(z^{(i)})}\mathrm{d}z^{(i)}\]

下面我们重点求\(\Lambda\)的估计公式。

首先将上式简化为:

\[\begin{align} &\sum_{i=1}^m\int_{z^{(i)}}Q_i(z^{(i)})\log\frac{p(x^{(i)}\mid z^{(i)};\mu,\Lambda,\Psi)p(z^{(i)})}{Q_i(z^{(i)})}\mathrm{d}z^{(i)} \\&=\sum_{i=1}^m\int_{z^{(i)}}Q_i(z^{(i)})\left[\log p(x^{(i)}\mid z^{(i)};\mu,\Lambda,\Psi)+\log p(z^{(i)})-\log Q_i(z^{(i)})\right]\mathrm{d}z^{(i)} \\&=\sum_{i=1}^m E_{z^{(i)}\sim Q_i}\left[\log p(x^{(i)}\mid z^{(i)};\mu,\Lambda,\Psi)+\log p(z^{(i)})-\log Q_i(z^{(i)})\right] \end{align}\]

去掉和各参数无关的部分后，可得：

\[\begin{align} &\sum_{i=1}^mE\left[\log p(x^{(i)}\mid z^{(i)};\mu,\Lambda,\Psi)\right] \\&=\sum_{i=1}^mE\left[\frac{1}{(2\pi)^{n/2}\lvert\Psi\rvert^{1/2}}\exp\left(-\frac{1}{2}(x^{(i)}-\mu-\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu-\Lambda z^{(i)})\right)\right] \\&=\sum_{i=1}^mE\left[-\frac{1}{2}\log\lvert\Psi\rvert-\frac{n}{2}\log(2\pi)-\frac{1}{2}(x^{(i)}-\mu-\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu-\Lambda z^{(i)})\right] \end{align}\]

去掉和\(\Lambda\)无关的部分，并求导可得：

\[\nabla_\Lambda\sum_{i=1}^m-E\left[\frac{1}{2}(x^{(i)}-\mu-\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu-\Lambda z^{(i)})\right]\tag{2}\]

因为公式2中\(E[\cdot]\)部分的结果实际上是个实数，因此该公式可变形为：

\[\nabla_\Lambda\sum_{i=1}^m-E\left[\operatorname{tr}\left(\frac{1}{2}(x^{(i)}-\mu-\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu-\Lambda z^{(i)})\right)\right]\]

而：

\[\begin{align} &\frac{1}{2}(x^{(i)}-\mu-\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu-\Lambda z^{(i)}) \\&=\frac{1}{2}\left[((x^{(i)}-\mu)^T-(\Lambda z^{(i)})^T)\Psi^{-1}((x^{(i)}-\mu)-\Lambda z^{(i)})\right] \\&=\frac{1}{2}\left[(x^{(i)}-\mu)^T\Psi^{-1}(x^{(i)}-\mu)-(x^{(i)}-\mu)^T\Psi^{-1}\Lambda z^{(i)} \\-(\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu)+(\Lambda z^{(i)})^T\Psi^{-1}\Lambda z^{(i)}\right] \end{align}\]

去掉和\(\Lambda\)无关的部分，可得：

\[\frac{1}{2}\left[(\Lambda z^{(i)})^T\Psi^{-1}\Lambda z^{(i)}-(x^{(i)}-\mu)^T\Psi^{-1}\Lambda z^{(i)}-(\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu)\right]\]

所以：

\[\begin{align} &\nabla_\Lambda\sum_{i=1}^m-E\left[\operatorname{tr}\left(\frac{1}{2}\left[(\Lambda z^{(i)})^T\Psi^{-1}\Lambda z^{(i)}-(x^{(i)}-\mu)^T\Psi^{-1}\Lambda z^{(i)}-(\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu)\right]\right)\right] \\&\begin{split}=\nabla_\Lambda\sum_{i=1}^m-E\left[\frac{1}{2}\operatorname{tr}\left((\Lambda z^{(i)})^T\Psi^{-1}\Lambda z^{(i)}\right)-\frac{1}{2}\operatorname{tr}\left((x^{(i)}-\mu)^T\Psi^{-1}\Lambda z^{(i)}\right) \\-\frac{1}{2}\operatorname{tr}\left((\Lambda z^{(i)})^T\Psi^{-1}(x^{(i)}-\mu)\right)\right]\end{split} \\&=\sum_{i=1}^m\nabla_\Lambda E\left[-\frac{1}{2}\operatorname{tr}\left(\Lambda^T \Psi^{-1}\Lambda z^{(i)}(z^{(i)})^T\right)+\operatorname{tr}\left(\Lambda^T \Psi^{-1}(x^{(i)}-\mu)(z^{(i)})^T\right)\right]\tag{3} \end{align}\]

因为：

\[\nabla_A\operatorname{tr}ABA^TC=CAB+C^TAB^T\]

所以：

\[\begin{align} &\nabla_A\operatorname{tr}\left(\Lambda^T \Psi^{-1}\Lambda z^{(i)}(z^{(i)})^T\right)=z^{(i)}(z^{(i)})^T\Lambda^T \Psi^{-1}+(z^{(i)}(z^{(i)})^T)^T\Lambda^T(\Psi^{-1})^T \\&=z^{(i)}(z^{(i)})^T\Lambda^T \Psi^{-1}+((z^{(i)})^T)^T(z^{(i)})^T\Lambda^T\Psi^{-1}=2z^{(i)}(z^{(i)})^T\Lambda^T \Psi^{-1} \end{align}\]

代入公式3，可得：

\[\sum_{i=1}^mE\left[-\Psi^{-1}\Lambda z^{(i)}(z^{(i)})^T+\Psi^{-1}(x^{(i)}-\mu)(z^{(i)})^T\right]\]

由上式等于0，可得：

\[\sum_{i=1}^m\Lambda E_{z^{(i)}\sim Q_i}\left[z^{(i)}(z^{(i)})^T\right]=\sum_{i=1}^m(x^{(i)}-\mu)E_{z^{(i)}\sim Q_i}\left[(z^{(i)})^T\right]\]

因此：

\[\Lambda=\left(\sum_{i=1}^m(x^{(i)}-\mu)E_{z^{(i)}\sim Q_i}\left[(z^{(i)})^T\right]\right)\left(\sum_{i=1}^m E_{z^{(i)}\sim Q_i}\left[z^{(i)}(z^{(i)})^T\right]\right)^{-1}\tag{4}\]

因为：

\[\operatorname{Cov}(Y)=E[YY^T]-E[Y]E[Y]^T\]

所以：

\[E[YY^T]=E[Y]E[Y]^T+\operatorname{Cov}(Y)\]

因此根据之前的讨论可得：

\[E_{z^{(i)}\sim Q_i}\left[(z^{(i)})^T\right]=\mu_{z^{(i)}\mid x^{(i)}}^T\] \[E_{z^{(i)}\sim Q_i}\left[z^{(i)}(z^{(i)})^T\right]=\mu_{z^{(i)}\mid x^{(i)}}\mu_{z^{(i)}\mid x^{(i)}}^T+\Sigma_{z^{(i)}\mid x^{(i)}}\]

将上式代入公式4，可得：

\[\Lambda=\left(\sum_{i=1}^m(x^{(i)}-\mu)\mu_{z^{(i)}\mid x^{(i)}}^T\right)\left(\sum_{i=1}^m \left(\mu_{z^{(i)}\mid x^{(i)}}\mu_{z^{(i)}\mid x^{(i)}}^T+\Sigma_{z^{(i)}\mid x^{(i)}}\right)\right)^{-1}\]

这里需要注意的是，和之前的混合高斯模型相比，我们不仅要计算\(\Sigma_{z^{(i)}\mid x^{(i)}}\)，还要计算\(E[z]\)和\(E[zz^T]\)。

此外，我们还可得出：（推导过程略）

\[\mu=\frac{1}{m}\sum_{i=1}^mx^{(i)}\] \[\begin{split}\Phi=\frac{1}{m}\sum_{i=1}^m\left(x^{(i)}(x^{(i)})^T-x^{(i)}\mu_{z^{(i)}\mid x^{(i)}}^T\Lambda^T-\Lambda\mu_{z^{(i)}\mid x^{(i)}}(x^{(i)})^T \\+\Lambda\left(\mu_{z^{(i)}\mid x^{(i)}}\mu_{z^{(i)}\mid x^{(i)}}^T+\Sigma_{z^{(i)}\mid x^{(i)}}\right)\Lambda^T\right)\end{split}\]

协同过滤的ALS算法

协同过滤概述

最近研究商品推荐系统的算法，因此，Andrew Ng讲义的内容，后续再写。

协同过滤是目前很多电商、社交网站的用户推荐系统的算法基础，也是目前工业界应用最广泛的机器学习领域。

协同过滤是利用集体智慧的一个典型方法。要理解什么是协同过滤 (Collaborative Filtering,简称CF)，首先想一个简单的问题，如果你现在想看个电影，但你不知道具体看哪部，你会怎么做？大部分的人会问问周围的朋友，看看最近有什么好看的电影推荐，而我们一般更倾向于从口味比较类似的朋友那里得到推荐。这就是协同过滤的核心思想。

如何找到相似的用户和物品呢？其实就是计算用户间以及物品间的相似度。以下是几种计算相似度的方法：

欧氏距离

\[d(x,y)=\sqrt{\sum(x_i-y_i)^2},sim(x,y)=\frac{1}{1+d(x,y)}\]

Cosine相似度

\[\cos(x,y)=\frac{\langle x,y\rangle}{\mid x\mid \mid y\mid }=\frac{\sum x_iy_i}{\sqrt{\sum x_i^2}~\sqrt{\sum y_i^2}}\]

这里有一个实现上需要注意的地方：

\(x^2\)不可以用pow(x,2)实现，因为这里的x有可能是负数。而负数的pow运算，计算机是不支持的。

皮尔逊相关系数（Pearson product-moment correlation coefficient，PPMCC or PCC）：

\[\begin{align} p(x,y)&=\frac{cov(X,Y)}{\sigma_X\sigma_Y}=\frac{\operatorname{E}[XY]-\operatorname{E}[X]\operatorname{E}[Y]}{\sqrt{\operatorname{E}[X^2]-\operatorname{E}[X]^2}~\sqrt{\operatorname{E}[Y^2]- \operatorname{E}[Y]^2}} \\&=\frac{n\sum x_iy_i-\sum x_i\sum y_i}{\sqrt{n\sum x_i^2-(\sum x_i)^2}~\sqrt{n\sum y_i^2-(\sum y_i)^2}} \end{align}\]

该系数由Karl Pearson发明。参见《机器学习（二）》中对Karl Pearson的简介。Fisher对该系数也有研究和贡献。

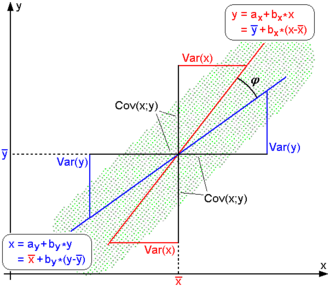
如上图所示，Cosine相似度计算的是两个样本点和坐标原点之间的直线的夹角，而PCC计算的是两个样本点和数学期望点之间的直线的夹角。

PCC能够有效解决，在协同过滤数据集中，不同用户评分尺度不一的问题。

参见：

https://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient

https://mp.weixin.qq.com/s/RjpH7XD5SCMkrSdcmG394g

从PCC到MIC，一文教你如何计算变量之间的相关性

Spearman秩相关系数（Spearman’s rank correlation coefficient）

对秩变量（ranked variables）套用PCC公式，即可得Spearman秩相关系数。

秩变量是一类不在乎值的具体大小，而只关心值的大小关系的统计量。

\(X_i\)	\(Y_i\)	\(x_i\)	\(y_i\)	\(d_i\)	\(d_i^2\)
86	0	1	1	0	0
97	20	2	6	-4	16
99	28	3	8	-5	25
100	27	4	7	-3	9
101	50	5	10	-5	25
103	29	6	9	-3	9
106	7	7	3	4	16
110	17	8	5	3	9
112	6	9	2	7	49
113	12	10	4	6	36

如上表所示，\(X_i\)和\(Y_i\)是原始的变量值，\(x_i\)和\(y_i\)是rank之后的值，\(d_i=x_i-y_i\)。

当\(X_i\)和\(Y_i\)没有重复值的时候，也可用如下公式计算相关系数：

\[r_s = {1- \frac {6 \sum d_i^2}{n(n^2 - 1)}}\]

Charles Spearman，1863～1945，英国心理学家。这个人的经历比较独特，20岁从军，15年之后退役。然后，进入德国莱比锡大学读博，中间又被军队征召，参加了第二次布尔战争，因此，直到1906年才拿到博士学位。伦敦大学学院心理学教授。
尽管他的学历和教职，都是心理学方面的。但他最大的贡献，却是在统计学领域。他也是因为在统计学方面的成就，得以当选皇家学会会员。
话说那个时代的统计学大牛，除了Fisher之外，基本都是副业比主业强。只有Fisher，主业方面也是那么牛逼，不服不行啊。

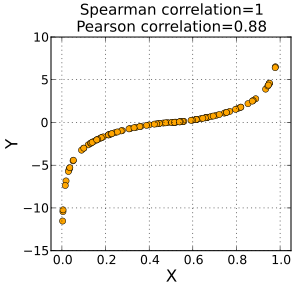
由上图可见，Pearson系数关注的是两个变量之间的线性相关度，而Spearman系数可以应用到非线性或者难以量化的领域。

参见：

https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient