ML » 机器学习（二）——分类与逻辑回归
2016-08-02 :: 6366 Words线性回归
LMS算法（续）
一些研究认为大Batch训练有可能无法达到最小值。
参考：
https://mp.weixin.qq.com/s/7sS-r6jIF4GAhZicBfFGDA
通过代码原理教你搞懂SGD随机梯度下降、BGD、MBGD
https://www.graphcore.ai/posts/revisiting-small-batch-training-for-deep-neural-networks
Revisiting Small Batch Training for Deep Neural Networks
正规方程组算法
正规方程组（Normal Equations）算法，是传统的以解方程的方式求最小值的方法。
如果，令
\[X=\begin{bmatrix} (x^{(1)})^T \\ (x^{(2)})^T \\ \vdots \\ (x^{(m)})^T \end{bmatrix}, \vec{y}=\begin{bmatrix} (y^{(1)}) \\ (y^{(2)}) \\ \vdots \\ (y^{(m)}) \end{bmatrix}\]则：
\[\theta=(X^TX)^{-1}X^T\vec{y}\]这种解方程的算法，实际上就是通常所说的最小二乘法（Least squares）。
优点：解是精确解，而不是近似解。不是迭代算法，程序实现简单。不在意\(X\)特征的scale。比如，特征向量\(X=\{x_1, x_2\}\), 其中\(x_1\)的range为1~2000，而\(x_2\)的range为1~4，可以看到它们的范围相差了500倍。如果使用梯度下降方法的话，会导致椭圆变得很窄很长，而出现梯度下降困难，甚至无法下降梯度（因为导数乘上步长后可能会冲到椭圆的外面）的问题。
缺点：维数高的时候，矩阵求逆运算的计算量很大。
这里的精确解指的是优化问题的精确解，而不是上述方程组的精确解。有效方程个数超过未知数个数的方程组，被称为超定方程组。超定方程组没有代数解，只有最小二乘解。解与实际方程的误差，又被称作残差。
插值问题
回归问题在数学上和插值问题是同一类问题。除了线性插值（回归）之外，还有多项式插值（回归）问题。
这里以一元函数为例，描述一下多项式插值问题。
对于给定的\(k+1\)个点\((x_0,y_0),\dots,(x_k,y_k)\)，求\(f(x)=\sum_{i=0}^ka_ix^i\)经过给定的\(k+1\)个点。显然\(k=1\)的时候，是线性插值。
多项式插值算法有很多种，最经典是以下两种：
1.拉格朗日插值算法（the interpolation polynomial in the Lagrange form）
\[L(x)=\sum_{j=0}^ky_jl_j(x),l_j(x)=\prod_{0\le m\le k\atop m\neq j}\frac{x-x_m}{x_j-x_m}\]2.牛顿插值算法（the interpolation polynomial in the Newton form）
\[N(x)=\sum_{j=0}^ka_jn_j(x),n_j(x)=\prod_{i=0}^{j-1}(x-x_i),a_j=[y_0,\dots,y_j]\]此外还有分段插值法，即将整个定义域分为若干区间，在区间内部进行线性插值或多项式插值。
欠拟合与过拟合
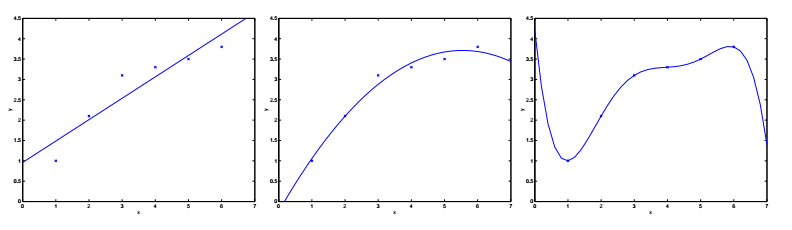
对于上图所示的6个采样点，采用线性回归时（左图），拟合程度不佳。如果采用二次曲线（中图）的话，效果就要好得多了。但也不是越多越好，比如五次曲线（右图）的情况下，虽然曲线完美的经过了6个采样点，但却偏离了实际情况——假设横轴表示房屋面积，纵轴表示房屋售价。
我们把左图的情况叫做欠拟合（Underfitting），右图的情况叫做过拟合（Overfitting）。
这里换个角度看：如果我们把上述多项式回归中的\(x,x^2,\dots,x^n\)看作是线性回归时的特征集的话，那么多项式回归就可以转化成为线性回归。
从中可以看出，欠拟合或过拟合实际上就是线性回归中的特征集选取问题。特征集选取不当，就会导致预测不准。
局部加权线性回归
局部加权线性回归（LWR，locally weighted linear regression）算法是一种对特征集选取不敏感的算法。它将公式2中的代价函数修改为：
\[J(\theta)=\frac{1}{2}\sum_{i=0}^m\omega^{(i)}(h_{\theta}(x^{(i)})-y^{(i)})^2 \tag{5}\]其中，\(\omega^{(i)}\)被称为权重，它有多种选取方法，最常用的是：
\[\omega^{(i)}=\exp\left(-\frac{(x^{(i)}-x)^2}{2\tau^2}\right)\]其中，\(\tau\)被称为带宽（bandwidth）。实际上，这就是一个高斯滤波器。离采样点x越近，其权重越接近1。
回归分析和相关分析的区别
回归分析是找出x和y之间的关系，而相关分析是找出x的各个分量之间的关系，和y并没有关系。
分类与逻辑回归
二分类
结果集y的取值只有0和1的分类问题被称为二分类，其中0被称为negative class，1被称为positive class，也可用“-”和“+”来表示。
逻辑回归
为了将线性回归的结果约束到\([0,1]\)区间，我们将公式1修改为：
\[h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} \tag{6}\]公式6又被称为logistic function或sigmoid function。函数\(g(z)\)的图像如下所示：
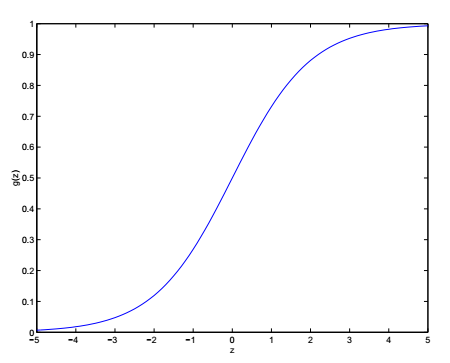
事实上，任何\([0,1]\)区间的平滑增函数，都可以作为\(g(z)\)，但公式6的好处在于
\[g'(z)=\frac{1}{(1+e^{-z})^2}e^{-z}=\frac{1}{(1+e^{-z})}\left(1-\frac{1}{(1+e^{-z})}\right)=g(z)(1-g(z))\tag{7}\]评估逻辑回归（Logistic regression）的质量，需要用到最大似然估计（maximum likelihood estimator）方法（由Ronald Aylmer Fisher提出）。最大似然估计是在“模型已定，参数未知”的情况下，寻找使模型出现的概率最大的参数集\(\theta\)的方法。显然，参数集\(\theta\)所确定的模型，其出现概率越大，模型的准确度越高。
最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的（independent and identically distributed，IID），即：
\[f(x_1,\dots,x_n;\theta)=f(x_1;\theta)\times \dots \times f(x_n;\theta)\]似然估计函数如下所示：
\[L(\theta)=\prod_{i=1}^mp(y^{(i)}\mid x^{(i)};\theta)\]Ronald Aylmer Fisher，1890～1962，英国人，毕业于剑桥大学。英国皇家学会会员，皇家统计学会主席。尽管他被称作“一位几乎独自建立现代统计科学的天才”，然而他的本职工作是遗传学。他最大的贡献是利用统计分析的方法，揭示了孟德尔的遗传定律在达尔文自然选择学说中的作用，为后来遗传物质DNA的发现奠定了理论基础。
虽然对于Fisher来说，数理统计只是他研究工作的一个副产品，但他在1925年所著《研究工作者的统计方法》（Statistical Methods for Research Workers），其影响力超过了半个世纪，几乎当代所有自然科学和社会科学领域都在应用他所创立的理论。F分布就是以他的名字命名的。
Karl Pearson，1857~1936，英国人，毕业于剑桥大学。英国皇家学会会员。发现了\(\chi^2\)分布。
William Sealy Gosset，1876~1937，英国人，毕业于牛津大学。笔名Student，发现了Student’s t-distribution。
这三人被后人合称现代统计学的三大创始人。他们都不是博士，毕业后从事的职业，也不是数学。Fisher和Pearson研究遗传学，Gosset研究化学。可见，统计学的诞生，有着很强的应用属性。
我们假设：
\[P(y=1\mid x;\theta)=h_\theta(x),P(y=0\mid x;\theta)=1-h_\theta(x)\]则该伯努利分布（Bernoulli distribution）的概率密度函数为：
\[p(y\mid x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y}\]其似然估计函数为：
\[L(\theta)=p(\vec{y}\mid X;\theta)=\prod_{i=1}^m(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}\]两边都取对数，得到对数化的似然估计函数：
\[\ell(\theta)=\log L(\theta)=\sum_{i=1}^my^{(i)}\log h_\theta(x^{(i)})+\sum_{i=1}^m(1-y^{(i)})\log(1-h_\theta(x^{(i)}))\] \[\frac{\partial \ell(\theta)}{\partial \theta_j}=(y-h_\theta(x))x_j\]按照随机梯度下降法，计算迭代公式：
\[\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)}))x^{(i)}_j\]可以看出，这和线性回归的迭代公式（公式4）完全相同。
\(g(z)\)还可以取以下函数（阶跃函数）：
\[g(z)=\begin{cases} 1, & z\ge 0 \\ 0, & z<0 \\ \end{cases}\]这时又被叫做感知器学习（perceptron learning）算法。
参考：
https://mp.weixin.qq.com/s/Y1_smqwmLPQzJ202JVq7zw
一文搞懂极大似然估计
https://mp.weixin.qq.com/s/MuV_kamfsUgcradKIaXGbw
逻辑回归（Logistic Regression）模型简介
https://mp.weixin.qq.com/s/YQ8l87EPw6EEhNy8MIU6Cg
区分识别机器学习中的分类与回归
http://blog.csdn.net/zengxiantao1994/article/details/72787849
极大似然估计详解
https://mp.weixin.qq.com/s/7_-a-suPO4qpAQVVJyz8BQ
概率论之概念解析：极大似然估计
https://mp.weixin.qq.com/s/vqYX1jpNsdw6F88a-CtZyw
什么是最大似然估计、最大后验估计以及贝叶斯参数估计
线性模型 vs. Logistic模型
线性回归模型的成立需满足以下几条假设：
\[Y_i=\beta_0+\beta_1X_i+\epsilon_i\] \[E(\epsilon_i)=0\] \[Var(\epsilon_i)=\sigma^2\] \[Cov(\epsilon_i, \epsilon_j)=0\] \[\epsilon_i \sim Normal\]二分类问题不满足第3条和第5条，但是有概率和为1的约束。
参考：
https://zhuanlan.zhihu.com/p/27149706
线性模型 vs. Logistic模型
指数类分布
线性回归和对数回归的迭代公式相同不是偶然的，它们都是指数类分布的特例。
指数类分布（exponential family distributions）的标准形式如下：
\[p(y;\eta)=b(y)\exp(\eta^TT(y)-a(\eta))\]其中，\(\eta\)被称作自然参数（natural parameter）或正准参数（canonical parameter），\(T(y)\)被称作充分统计量（sufficient statistic）。
\(a(\eta)\)是对数配分函数（log partition function），它存在的目的是利用\(e^{-a(\eta)}\)进行约束，以使:
\[\sum_Y p(y;\eta)=1或\int_Y p(y;\eta)=1\]伯努利分布到指数类分布的变换过程如下：
\[\begin{align}p(y:\phi)&=\phi^y(1-\phi)^{1-y}=\exp(\log(\phi^y(1-\phi)^{1-y})) \\&=\exp(y\log(\phi)+(1-y)\log(1-\phi)) \\&=\exp(y\log(\frac{\phi}{1-\phi})+\log(1-\phi)) \end{align}\]可见：
\[\begin{align}& b(y)=1 \\& \eta=\log(\frac{\phi}{1-\phi})\Rightarrow \phi=\frac{1}{1+e^{-\eta}} \\& T(y)=y \\& a(\eta)=-\log(1-\phi) \\\end{align}\]其中，\(\log(\frac{\phi}{1-\phi})\)被称为Logit函数，从上面的推导可看出，它和sigmoid函数是有相当深的渊源的。
高斯分布到指数类分布的变换过程如下：
\[\begin{align}p(y;\mu)&=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}(y-\mu)^2\right) \\&=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}y^2\right)\cdot\exp\left(\mu y-\frac{1}{2}\mu^2\right)\dot\ \end{align}\]可见：
\[\begin{align}& \eta=\mu \\& T(y)=y \\& a(\eta)=\frac{\mu^2}{2} \\& b(y)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}y^2\right) \\\end{align}\]除此之外，Dirichlet分布、Poisson分布、多项分布、\(\beta\)分布、\(\gamma\)分布都是指数类分布。
您的打赏，是对我的鼓励
