Antkillerfarm Hacking V7.0

Graph ML（一）——图论基础, 社交网络

2020-05-29

图论基础

基本概念

图(Graph)，是一种由若干个结点(Node)及连接两个结点的边(Edge)所构成的图形，用于刻画不同结点之间的关系。

以下术语，每组均为同义词，下文将不加区分的任意使用：

Objects: nodes, vertices –> V

Interactions: links, edges –> E

System: network, graph –> G(V,E)

Network, node, link偏重于现实中的系统，而Graph, vertex, edge就是纯数学的表示了。

Graph非常适合用于描述non-Euclidean space的数据：

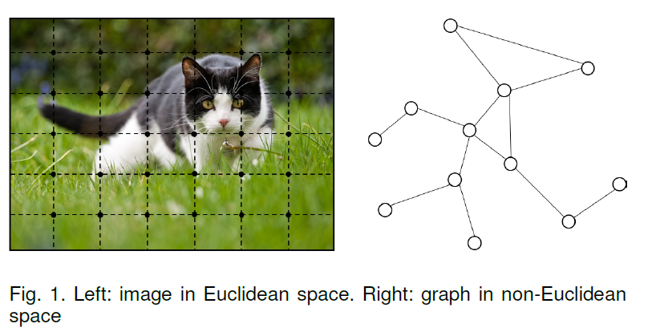
与Network相关的任务主要包括：

  • Node classification：预测结点的类型。

  • Link prediction：预测两个结点的连接性。

  • Community detection：识别有密切关系的结点簇（clusters）。

  • Network similarity：度量两个Node/Network的相似性。

BFS：Breadth First Search

DFS：Depth First Search

Node Embedding：将结点映射到高维空间，以使相似的结点，距离也较近。

Node Degree：结点的边的数量。对于有向图还可分为in-degree和out-degree。

Complete Graph：在N个结点的图中，任意一个结点都和其他结点连接。显然在相同结点数的图中，完全图的边数最多：\(E_{max}=\frac{N(N-1)}{2}\)。

Bipartite Graph：

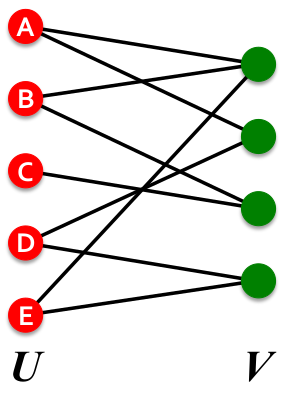
上图中结点被分为U、V两个子集，且每条边都是一个U中的结点连接上一个V中的结点。

Bipartite Graph典型例子是演员-电影关系图，显然演员是一个子集，而电影是另一个子集。

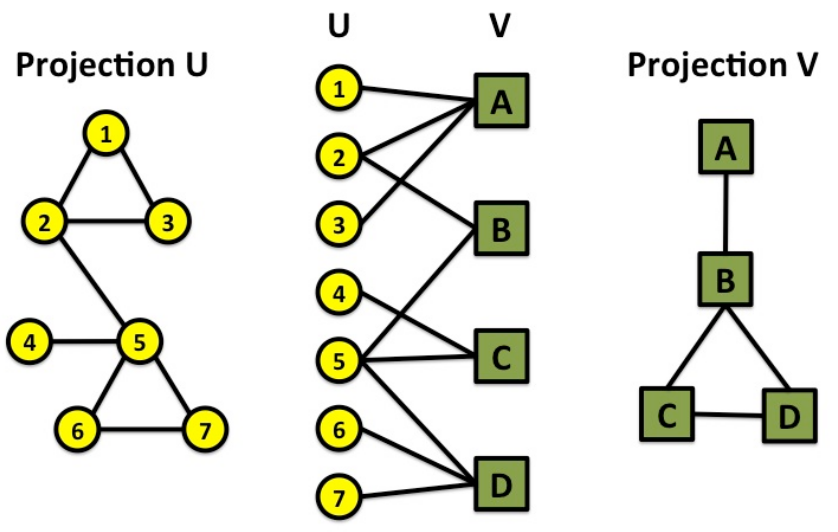
如上图，Bipartite Graph可被用来进行图结构的变换。

图的表示方法：

  • Adjacency Matrix

  • Adjacency List

  • Edge List

对于真实的网络来说，每个结点的邻接结点数量一般远小于网络的结点数N，即\(E\ll E_{max}\)。这种情况下，图的邻接矩阵是一个稀疏矩阵，因此采用Adjacency List/Edge List会更有效率一些。

除了标准图之外，还有若干图的变种：

  • Weighted：边有权重属性的图。

  • Self-edges (self-loops)：结点和自己之间有边的图。

  • Multigraph：两个结点间有不止一个边的图。

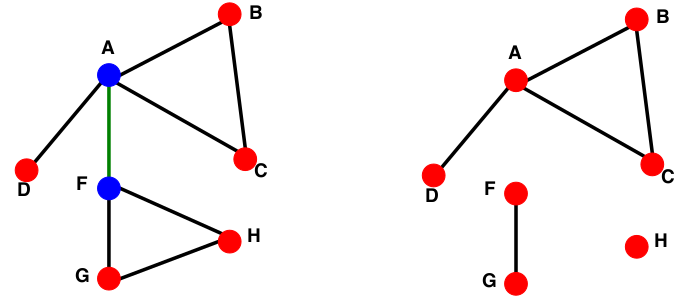
上左图中，绿色的边去掉之后，图就不连通了，这样的边被称为Bridge edge。

上左图中，蓝色的结点去掉之后，图就不连通了，这样的结点被称为Articulation node。

对于有向图来说，它的连通性有如下术语：

Strongly connected directed graph：图中任意两点A、B之间，既有A->B的路径，也有B->A的路径。这里的路径可以是两点间的直接连接，也可以是路过其他点的间接连接。

Weakly connected directed graph：图中至少有两点间，只有单向的路径。

Strongly connected components (SCCs)：一个图的所有子图中，满足强连通条件的子图。

In-component：能够到达SCC的结点，被称为该SCC的In-component。类似的还有Out-component。

Network Properties

Network Properties是一些用于定量描述Network的指标。常见的主要有：

  • Degree distribution：P(k)

\[P(k)=N_k/N\]

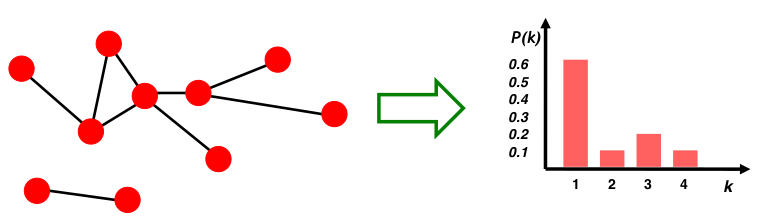
其中，\(N_k\)表示degree为k的结点的数量。

  • Path length：h

沿着图中的边的方向，从一个结点到另一个相邻结点的行为被称为Step Walk。

Path：一系列连续的Step Walk所形成的结点序列。

Path通常有两种表示方式：

结点表示：\(P_n = \{i_0 ,i_1 ,i_2 ,\dots,i_n \}\)

边表示：\(P_n = \{(i_0 ,i_1 ),(i_1 ,i_2 ),(i_2 ,i_3 ),\dots,(i_{n-1} ,i_n )\}\)

序列中边的个数被称为Path length。

一条路径可以经过同一个顶点或同一条边若干次。

如果路径上的各顶点均不重复，则称这样的路径为Simple path。如果路径上的第一个顶点与最后一个顶点重合，这样的路径称为回路(cycle)或环或圈。

两点间长度最短的路径被称为shortest path。shortest path的长度被称为两点间的Distance。两个不连接结点间的距离，通常定义为正无穷。

对于有向图来说，\(h_{B,C}\)通常不等于\(h_{C,B}\)。

图中所有结点间距离的最大值，被称为Diameter。

强连通图中，所有结点间距离的平均值，被称为Average path length。

\[\overline h = \frac{1}{2E_{max}}\sum_{i,j\neq i}h_{ij}\]
  • Clustering coefficient：C
\[C_i=\frac{2e_i}{k_i(k_i-1)}\]

其中，\(e_i\)表示结点i的邻居之间的边的个数。\(k_i\)表示i的degree。

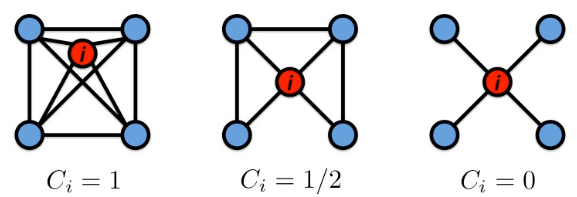
以上左图为例，i结点有4个邻居，也就是\(k_i\)为4。这些邻居之间有6条边，即\(e_i\)为6。综上可得，\(C_i=1\)。

由于\(k_i(k_i-1)\)是完全有向图的边数，所以\(C_i\in [0,1]\)。

图中所有结点的\(C_i\)平均值被称为Average clustering coefficient：

\[C=\frac{1}{N}\sum_i^N C_i\]
  • Connected components：s

这里用s表示图中最大的连通子图（Largest component / Giant component）的结点数。

Erdös-Renyi Random Graph Model

上面讲述了图的统计特性，反过来给定了统计特性，我们也可以生成相应的图。这种生成图的方法通常称为Erdös-Renyi Random Graph Model。

1959～1968年，数学家Paul Erdos和Alfred Renyi发表了关于随机图（Random Graph）的一系列论文，在图论的研究中融入了组合数学和概率论，建立了一个全新的数学领域分支—随机图论。

Alfréd Rényi，1921～1970，匈牙利数学家。University of Szeged博士（1947）。匈牙利科学院院士，创建了匈牙利科学院数学研究所。1944年进过纳粹集中营。

Paul Erdös，1913～1996，匈牙利数学家。Péter Pázmány University博士（1934）。匈牙利科学院院士，美国科学院院士，英国皇家学会会员。Cole Prize（1951）。Wolf Prize（1984）。

我们用\(G_{np}\)表示n个结点的无向图中，每个边出现的概率是p。用\(G_{nm}\)表示n个结点的无向图中，随机均匀的选择m个边。

由于这是一个随机选择的过程，因此同样的n和p可以对应很多组不同的图。

对于\(G_{np}\)来说，由于每条边只有选择和不选择两种可能，因此总的来看，它的Degree distribution满足二项分布。即：

\[P(k) = \binom {n-1} k p^k(1-p)^{n-1-k}\]

这里使用n-1，而不是n，主要是因为：对于n个结点的图来说，每个结点最多只能有n-1条边。

k的均值为：\(\overline{k}=p(n-1)\)

\[\]

参考：

https://zhuanlan.zhihu.com/p/300861555

随机图模型

谱聚类

谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

http://www.cnblogs.com/pinard/p/6221564.html

谱聚类（spectral clustering）原理总结

https://mp.weixin.qq.com/s/DrD7aONVfN3Ibx4x6z-e3Q

理解谱聚类

https://zhuanlan.zhihu.com/p/266604288

图中的谱聚类详解

https://mp.weixin.qq.com/s/-knVcuS-GdbtyK63snrWog

到底什么是谱聚类算法？

Laplacian matrix

https://mp.weixin.qq.com/s/iZLwlmBuXWrbpzvkm8nOrw

拉普拉斯矩阵和瑞利熵

https://mp.weixin.qq.com/s/WYiWGtedfR4kryztvJKyRw

谱聚类方法推导和对拉普拉斯矩阵的理解

https://zhuanlan.zhihu.com/p/85287578

拉普拉斯矩阵与拉普拉斯算子的关系

https://mp.weixin.qq.com/s/87i2u2ZKqSxG_1-dK_Hv1w

理解图的拉普拉斯矩阵

Pearce-Kelly算法

Pearce-Kelly算法是检测DAG，并进行拓扑排序的算法。

https://www.doc.ic.ac.uk/~phjk/Publications/DynamicTopoSortAlg-JEA-07.pdf

A Dynamic Topological Sort Algorithm for Directed Acyclic Graphs

https://blog.csdn.net/qinzhaokun/article/details/48541117

拓扑排序的两种实现：Kahn算法和dfs算法

参考

https://mp.weixin.qq.com/s/LqCfwf90bzZKVMLLY5dbXA

图数据分析与可视化，538页pdf

https://mp.weixin.qq.com/s/gn9FePRvg5_luE7vEWbgvw

图理论与应用，270页pdf

https://mp.weixin.qq.com/s/7yPdA575qToHh0HQ_Zfc9Q

最新《图理论》笔记书，98页pdf

https://mp.weixin.qq.com/s/zOdy-1vCJD_dPFSoe0ELFA

图论与图学习（一）：图的基本概念

https://mp.weixin.qq.com/s/0ZdS1WOSDZiXnxP8fybBAw

图论与图学习（二）：图算法

https://mp.weixin.qq.com/s/BkKw2C3n9WsmIchJkkZxUw

从七桥问题开始：全面介绍图论及其应用

https://mp.weixin.qq.com/s/ZDY3Yt67eXK5pjXgvJkkyQ

图论的各种基本算法

https://mp.weixin.qq.com/s/2h1dgvPbYKBOYZPiixg9iw

手把手：四色猜想、七桥问题…程序员眼里的图论，了解下？

https://mp.weixin.qq.com/s/ra9v1pgFsbOcJrtONoZNvQ

图论基础与图存储结构

https://mp.weixin.qq.com/s/Y7qZlJdJ8fav5BXFGwdSOQ

Graph Analysis and Its Application

https://mp.weixin.qq.com/s/VdvvQetxAvkiNF04hV9PeA

图搜索算法介绍(RRT/RRT*)

https://mp.weixin.qq.com/s/oqdB1vmkGtAtjEHoBhgwiA

最快速的寻路算法Jump Point Search

https://mp.weixin.qq.com/s/dTI3BdgixVTAFsnxtKjq0A

常见图算法介绍

https://mp.weixin.qq.com/s/dsPiw-n8iclT8uWkeTiBUA

图数据表征学习，绝不止图神经网络一种方法

https://mp.weixin.qq.com/s/0Iih4TBYUIPY5R4LfWxUNQ

10种常用的图算法直观可视化解释

https://mp.weixin.qq.com/s/0nC9Sc1xi9VBjyJSGtUfHA

2020图核方法最新进展与未来挑战，151页pdf

https://mp.weixin.qq.com/s/GT1WrG2c6OGrXUH8BGWu8g

Weisfeiler-Leman算法

https://mp.weixin.qq.com/s/cDB615hkHBdHqNV06DSWBQ

什么是度，什么是握手定理

https://mp.weixin.qq.com/s/YSvn17Xlm3M7RRRIR4He-A

图神经网络：数学基础篇

https://mp.weixin.qq.com/s/09CyHZqG2D6gKjiBaVwyyg

什么是图距离

https://mp.weixin.qq.com/s/rneDYqi_sfTCx0vljN1u4g

什么是度分布

社交网络

信息传播模型

感染模型

SI、SIR等模型。

https://www.cnblogs.com/scikit-learn/p/6937326.html

基本的传染病模型：SI、SIS、SIR及其Python代码实现

https://blog.csdn.net/robin_Xu_shuai/article/details/73699207

SI疾病传播模型实现

影响力模型

IC、LT等模型。

https://blog.csdn.net/asialee_bird/article/details/79673418

社交网络影响力最大化

http://cjc.ict.ac.cn/online/onlinepaper/wzj-201672182158.pdf

基于社交内容的潜在影响力传播模型

Antkillerfarm
antkillerfarm@sohu.com

github.com/antkillerfarm

Fork me on GitHub