• 社交网络（续）
  • 链接预测
  • 社区发现
  • Social Listening
  • 其他
• PageRank算法
  • 概述
  • 马尔可夫链
  • 简易推导
  • TextRank
  • HITS

社交网络（续）

链接预测

Link Prediction是指如何通过已知的网络节点以及网络结构等信息预测网络中尚未产生连边的两个节点之间产生链接的可能性。这种预测既包含了对未知链接（exist yet unknown links）的预测也包含了对未来链接（future links）的预测。该问题的研究在理论和应用两个方面都具有重要的意义和价值。

http://www.docin.com/p-810499317.html

社交网络中的链接预测研究

社区发现

社区发现（Community Detection）算法用来发现网络中的社区结构，也可以视为一种广义的聚类算法。

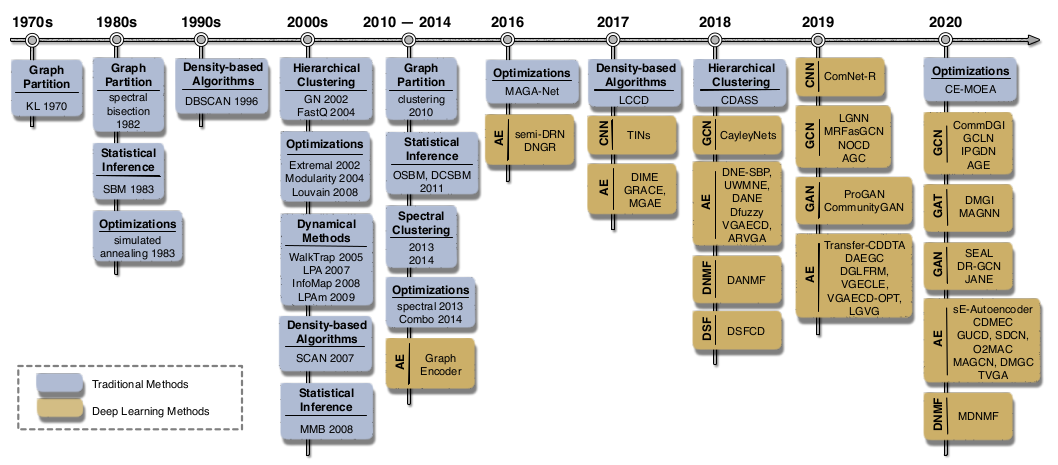
https://blog.csdn.net/itplus/article/details/9286905

Community Detection算法

https://mp.weixin.qq.com/s/wR5FQKRjYwt29Qis9wnNrw

基于深度学习的社区发现最新综述

https://mp.weixin.qq.com/s/wYA_6PPqrV24FE2KMU_l5g

网络社团发现新综述：从统计建模到深度学习

https://www.zhihu.com/question/29042018

社区发现(Community detection)的经典方法有哪些？该领域最新的研究进展如何？

http://www.mapequation.org/index.html

这是一个复杂网络方面的网站，提供了很多算法的代码。例如infomap

https://www.cnblogs.com/nolonely/p/6262508.html

社区发现算法总结（一）

https://www.cnblogs.com/nolonely/p/6268150.html

社区发现算法总结（二）

https://sikasjc.github.io/2017/12/20/GN/

GN算法–复杂网络中社区发现与Python实现

https://www.cnblogs.com/LittleHann/p/9078909.html

社区发现算法-Fast Unfolding（Louvian）算法初探

http://blog.sina.com.cn/s/blog_617032070100er0r.html

Infomap算法描述

https://mp.weixin.qq.com/s/S0vUBFCfizjVe_L4SIrGqQ

网络新闻真假难辨？机器学习来助你一臂之力

https://mp.weixin.qq.com/s/2aKc4yM0b52X-SViGQycwA

大规模网络的社区检测和排序问题综述

https://mp.weixin.qq.com/s/_HOdAo2ClhJqbUrDvsc-3w

Philip S. Yu团队最新综述！社区发现的深度学习方法：进展、挑战、机遇

https://mp.weixin.qq.com/s/uA8z5id8_py3GC_IxcceKA

Philip S. Yu等最新“深度学习社区检测”大综述论文，28页pdf174篇文献概述六大类深度社区检测方法

https://mp.weixin.qq.com/s/HGpay4KZwtz7t5QBIeE8Rg

图机器学习经典算法louvain完全解读

https://zhuanlan.zhihu.com/p/262235147

图网络中的社群以及相关社群发现算法

https://mp.weixin.qq.com/s/TLX2bZHhJ7LqI9k1w1JF7w

实现、动态展示多种社区发现算法，这个Python库（communities）助你发现网络图的社区结构

Social Listening

企业们通过捕捉网络上与品牌/产品/营销事件相关的关键词，去监测消费者都对品牌/产品/营销事件说了什么的行为，被称作社会化聆听（Social Listening）。

https://mp.weixin.qq.com/s/htzfVSv3V8b00vae6nKm-A

如何利用Social Listening从社会化媒体中“提炼”有价值的信息？

https://mp.weixin.qq.com/s/0khbV1yOFZ5vNLZPRKYA6g

Social Listening和传统市场调研的关系是怎样的？

https://mp.weixin.qq.com/s/QrI23je3HqCFYkeVb9af8g

如何利用Social Listening从在线垂直社区提炼有价值的信息—以汽车之家的口碑数据挖掘为例

其他

https://mp.weixin.qq.com/s/Xp3BQA91dN73PiSWQd0Avw

深度学习技术在社会化推荐场景中的总结

PageRank算法

概述

在PageRank提出之前，已经有研究者提出利用网页的入链数量来进行链接分析计算，这种入链方法假设一个网页的入链越多，则该网页越重要。早期的很多搜索引擎也采纳了入链数量作为链接分析方法，对于搜索引擎效果提升也有较明显的效果。

PS：百度李彦宏当时提出的算法，大致就在这个层次。然而他不会想到，世上还有“交换链接”这样的商业互吹行为。这种只重数量，忽视质量的方法，显然是有很大破绽的。

PageRank除了考虑到入链数量的影响，还参考了网页质量因素，两者相结合获得了更好的网页重要性评价标准。

对于某个互联网网页A来说，该网页PageRank的计算基于以下两个基本假设：

数量假设：在Web图模型中，如果一个页面节点接收到的其他网页指向的入链数量越多，那么这个页面越重要。

质量假设：指向页面A的入链质量不同，质量高的页面会通过链接向其他页面传递更多的权重。所以越是质量高的页面指向页面A，则页面A越重要。

利用以上两个假设，PageRank算法刚开始赋予每个网页相同的重要性得分，通过迭代递归计算来更新每个页面节点的PageRank得分，直到得分稳定为止。PageRank计算得出的结果是网页的重要性评价，这和用户输入的查询是没有任何关系的，即算法是主题无关的。

优点：

这是一个与查询无关的静态算法，所有网页的PageRank值通过离线计算获得；有效减少在线查询时的计算量，极大降低了查询响应时间。

缺点：

1）人们的查询具有主题特征，PageRank忽略了主题相关性，导致结果的相关性和主题性降低。

2）旧的页面等级会比新页面高。因为即使是非常好的新页面也不会有很多上游链接，除非它是某个站点的子站点。

马尔可夫链

Markov链的基本定义参见《机器学习（二十六）》。

这里补充一些定义：

定义1：设C为状态空间的一个子集，如果从C内任一状态i不能到C外的任何状态，则称C为闭集。除了整个状态空间之外，没有别的闭集的Markov链被称为不可约的。

如果用状态转移图表示Markov链的话，上面的定义表征了Markov链的连通性。

定义2：如果有正整数d，只有当\(n=d,2d,\dots\)时，\(P_{ii}^{(n)}>0\)，或者说当n不能被d整除时，\(P_{ii}^{(n)}=0\)，则称i状态为周期性状态。如果除了\(d=1\)之外，使\(P_{ii}^{(n)}>0\)的各n值没有公约数，则称该状态i为非周期性状态。

这个定义表征了Markov链各状态的独立性。

定义3：

\[f_{ij}^{(n)}=P(X_{m+v}\neq j,X_{m+n}=j|X_m=i)\]

其中，\(n>1,1\le v\le n-1\)。

上式表示由i出发，首次到达j的概率，也叫首中概率。

相应的还有最终概率：

\[f_{ij}=\sum_{n=1}^\infty f_{ij}^{(n)}\]

定义4：

如果\(f_{ii}=1\), 则称状态i为常返的，如果\(f_{ii}<1\), 则称状态i为非常返的。

令\(u_i=\sum_{n=1}^\infty nf_{ii}^{(n)}\)，则\(u_i\)表示由i出发i，再返回i的平均返回时间。

如果\(u_i=\infty\)，则称i为零常返的。

常返态表征Markov链的极限分布。显然如果长期来看，状态i“入不敷出”的话，则其最终的极限概率为0。

根据上面的定义，还可得到Markov链的三个推论：

推论1：有限状态的不可约非周期Markov链必存在平稳分布。

推论2：若不可约Markov链的所有状态是非常返或零常返的，则不存在平稳分布。

推论3：若\(X_j\)是不可约的非周期的Markov链的平稳分布，则\(\lim_{n\to\infty}P_{ij}^{(n)}=X_j\)，即极限分布等于平稳分布。

简易推导

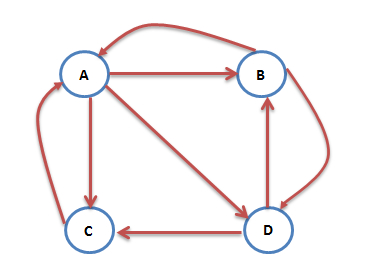
上图是一个Web图模型的示例。其中的节点表示网页，箭头表示网页链接。因此，从图论的角度来说，这是一个有向图。而从随机过程的角度，这也可以看做是一个Markov链。

上图中，A有两个入链B和C，则：

\[PR(A)=PR(B)+PR(C)\]

然而图中除了C之外，B和D都不止有一条出链，所以上面的计算式并不准确：

\[PR(A) = \frac{PR(B)}{2} + \frac{PR(C)}{1}\]

一般化，即：

\[PR(A)= \frac{PR(B)}{L(B)}+ \frac{PR(C)}{L(C)}\]

其中，L表示外链个数。

更一般化，可得：

\[PR(u) = \sum_{v \in B_u} \frac{PR(v)}{L(v)}\]

这里有两种异常情况需要处理。

1.互联网中不乏一些没有出链的网页，为了满足Markov链的收敛性，设定其对所有的网页（包括它自己）都有出链。

2.互联网中一个网页只有对自己的出链，或者几个网页的出链形成一个循环圈。那么在不断地迭代过程中，这一个或几个网页的PR值将只增不减，显然不合理。

对于这种情况，我们假定有一个确定的概率\(\alpha\)会输入网址直接跳转到一个随机的网页，并且跳转到每个网页的概率是一样的。即：

\[PR(p_{i}) = \alpha \sum_{p_{j} \in M_{p_{i}}} \frac{PR(p_{j})}{L(p_{j})} + \frac{(1 - \alpha)}{N}\]

\(\alpha\)也叫阻尼系数，一般设定为0.85。

由Markov链的收敛性可知，无论每个网页的PR初始值如何设定，都不影响最终的PR值。

在实际计算中，由于网页数量众多，而其中的链接关系相对较少，因此这个计算过程，实际上是一个巨维稀疏矩阵的凸优化问题，此处不再赘述。

TextRank

TextRank算法是PageRank算法在NLP领域的扩展，被广泛用于自动摘要和提取关键词。

将原文本拆分为句子，在每个句子中过滤掉停用词（可选），并只保留指定词性的单词（可选）。由此可以得到句子的集合和单词的集合。

每个单词作为TextRank中的一个节点。假设一个句子依次由下面的单词组成：\(w_1,\dots,w_n\)。从中取出k个连续的单词序列，组成一个窗口。我们认为窗口中任意两个单词间存在一个无向边，从而构建出一个图模型。

对该图模型应用PageRank算法，可得：

\[WS(V_i)=(1-d)+d\sum_{V_j \in In(V_i)}\frac{w_{ji}}{\sum_{V_k \in Out(V_j)}w_{jk}}WS(V_j)\]

上式的W为权重（也可叫做结点相似度），一般采用以下定义：

\[W(S_i,S_j)=\frac{|\{w_k|w_k\in S_i \& w_k\in S_j\}|}{\log(|S_i|)+\log(|S_j|)}\]

其中，\(\mid S_i\mid\)是句子i的单词数。

上面说的是关键词的计算方法。计算自动摘要的时候，将句子定义为结点，并认为全部句子都是相邻的即可。自动摘要所用的权重函数，一般采用BM25算法。

HITS

HITS算法和PageRank算法可以看作兄弟算法。因为他们是同时期提出的对网页进行排序的两种算法。并且他们的原理有相似之处，都考虑了权威性网站的作用。

但这两种算法也有区别：

• HITS计算每个网页的权威值和枢纽值，将二者分开考虑。而PageRank只计算PageRank值。

• HITS只处理与关键词相关的网页集合，范围很小。而PageRank是全局算法，会计算互联网中所有网页的PageRank值。

因为上一点的缘故，HITS算法更适合部署在客户端，而PageRank更适合部署在服务器端。

参考：

https://mp.weixin.qq.com/s/9g174YP-M2HWsPR-9ikgcg

什么是HITS算法