• Vanilla GAN
  • 通俗解释
  • 基本原理
  • 伪造者
  • 正样本分布
  • KL散度
  • JS散度
  • 神经距离
  • 如何对抗
    • Step1
    • Step2

Vanilla GAN

GAN是“生成对抗网络”（Generative Adversarial Networks）的简称，由2014年还在蒙特利尔读博士的Ian Goodfellow引入深度学习领域。

Ian J. Goodfellow，斯坦福大学本硕+蒙特利尔大学博士。导师是Yoshua Bengio。现为Google研究员。
个人主页：
http://www.iangoodfellow.com/

论文：

《Generative Adversarial Nets》

教程：

https://deepgenerativemodels.github.io

CS 236: Deep Generative Models

李宏毅的DL课程中也有GAN的章节，篇幅还不短。

Goodfellow相关资源：

http://www.iangoodfellow.com/slides/2016-12-04-NIPS.pdf

Goodfellow的历年演讲：（基本全是GAN，没啥新领域。。。）

https://mp.weixin.qq.com/s/GobKiuxgZv0-ufSRBpTcIA

Ian Goodfellow ICCV2017演讲：解读GAN的原理与应用

https://mp.weixin.qq.com/s/NDZPPA-0FhqSzRndQOhNEw

Google GAN之父Ian Goodfellow 最新演讲：生成对抗网络介绍

https://mp.weixin.qq.com/s/b8g_wNqi4dD5x9whj9ZN4A

争议、流派，有关GAN的一切：Ian Goodfellow Q&A

https://mp.weixin.qq.com/s/RYMvgbOgZYjMOIxygpYWSQ

Ian GoodFellow ICLR 2019演讲：对抗机器学习的进展与挑战

https://mp.weixin.qq.com/s/LL6kheCrJ07PtJ6NleIKTA

IanGoodfellow自注意力GAN的代码与PPT

通俗解释

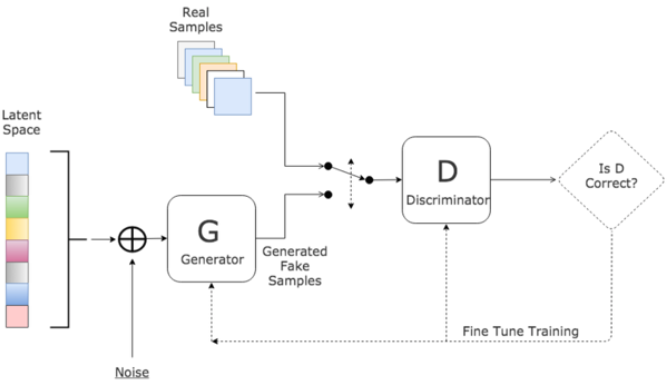
对于GAN来说，最通俗的解释就是“伪造者-鉴别者”的解释，如艺术画的伪造者和鉴别者。一开始伪造者和鉴别者的水平都不高，但是鉴别者还是比较容易鉴别出伪造者伪造出来的艺术画。但随着伪造者对伪造技术的学习后，其伪造的艺术画会让鉴别者识别错误；或者随着鉴别者对鉴别技术的学习后，能够很简单的鉴别出伪造者伪造的艺术画。这是一个双方不断学习技术，以达到最高的伪造和鉴别水平的过程。

从上面的解释可以看出，GAN实际上是一种零和游戏上的无监督算法。

基本原理

上面的解释虽然通俗，却并未涉及算法的实现。要实现上述原理，至少要解决三个问题：

1.什么是伪造者。

2.什么是鉴别者。

3.如何对抗。

以下文章的组织顺序，主要参考下文：

http://kexue.fm/archives/4439/

互怼的艺术：从零直达WGAN-GP

还有李宏毅的课程。

老规矩，摘要+点评。

伪造者

伪造者在这里实际上是一种Generative算法。伪造的内容是：将随机噪声映射为我们所希望的正样本。

随机噪声我们一般定义为均匀分布，于是上面的问题可以转化为：如何将均匀分布X映射为正样本分布Y。

首先，我们思考一个简单的问题：如何将\(U[0,1]\)映射为\(N(0,1)\)？

理论上的做法是：将\(X∼U[0,1]\)经过函数\(Y=f(X)\)映射之后，就有\(Y∼N(0,1)\)了。设\(\rho(x)\)是\(U[0,1]\)是概率密度函数，那么\([x,x+dx]\)和\([y,y+dy]\)这两个区间的概率应该相等，而根据概率密度定义，\(\rho(x)\)不是概率，\(\rho(x)dx\)才是概率，因此有：

\[\rho(x)dx=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{y^2}{2}\right)dy\]

即：

\[\int_{0}^x \rho(t)dt=\int_{-\infty}^{y}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{t^2}{2}\right)dt=\Phi(y)\]

其中，\(\Phi(y)\)是标准正态分布的累积分布函数，所以

\[y=\Phi^{-1}\left(\int_0^x \rho(t)dt\right)\]

注意到累积分布函数是无法用初等函数显式表示出来的，更不用说它的逆函数了。说白了，\(Y=f(X)\)的f的确是存在的，但很复杂，以上解只是一个记号，该算的还是要用计算机算。

正态分布是常见的、相对简单的分布，但这个映射已经这么复杂了。如果换了任意分布，甚至概率密度函数都不能显式写出来，那么复杂度可想而知～

考虑到我们总可以用一个神经网络来拟合任意函数。这里不妨用一个带有多个参数的神经网络\(G(X,\theta)\)去拟合f？只要把参数\(\theta\)训练好，就可以认为\(Y=G(X,\theta)\)了。这里的G是Generator的意思。

正样本分布

如上所述，一般的正样本（Real Samples）分布是很难给出概率密度函数的。然而，我们可以换个角度思考问题。

假设有一批服从某个指定分布的数据\(Z=(z_1,z_2,\dots,z_N)\)，根据概率论的相关定义，我们至少可以使用离散采样的方法，根据Z中的样本分布，来近似求出Z的指定分布。下文如无特殊指出，均以Z中的样本分布来代替Z的指定分布，简称Z的分布。

那么接着就有另一个问题：如何评估\(G(X,\theta)\)生成的样本的分布和Z的分布之间的差异呢？

KL散度

比较两个分布的差异的最常用指标是KL散度。其定义参见《机器学习（九）》。

JS散度

因为KL散度不是对称的，有时候将它对称化，即得到JS散度（Jensen–Shannon divergence）：

\[JS\Big(p_1(x),p_2(x)\Big)=\frac{1}{2}KL\Big(p_1(x)\|p_2(x)\Big)+\frac{1}{2}KL\Big(p_2(x)\|p_1(x)\Big)\]

Claude Elwood Shannon，1916～2001，美国数学家，信息论之父。密歇根大学双学士+MIT博士。先后供职于贝尔实验室和MIT。

KL散度和JS散度，也是Ian Goodfellow在原始GAN论文中，给出的评价指标。

虽然KL散度和JS散度，在这里起着距离的作用，但它们不是距离，它们不满足距离的三角不等式，因此只能叫“散度”。

神经距离

假设我们可以将实数域分成若干个不相交的区间\(I_1,I_2,\dots,I_K\)，那么就可以估算一下给定分布Z的概率分布：

\[p_z(I_i)=\frac{1}{N}\sum_{j=1}^{N}\#(z_j\in I_i)\]

其中\(\#(z_j\in I_i)\)表示如果\(z_j\in I_i\)，那么取值为1，否则为0。

接着我们生成M个均匀随机数\(x_1,x_2,\dots,x_M\)（这里不一定要\(M=N\)，还是那句话，我们比较的是分布，不是样本本身，因此多一个少一个样本，对分布的估算也差不了多少。），根据\(Y=G(X,\theta)\)计算对应的\(y_1,y_2,\dots,y_M\)，然后根据公式可以计算：

\[p_y(I_i)=\frac{1}{M}\sum_{j=1}^{M}(y_j\in I_i)\]

现在有了\(p_z(I_i)\)和\(p_y(I_i)\)，那么我们就可以算它们的差距了，比如可以选择JS距离

\[\text{Loss} = JS\Big(p_y(I_i), p_z(I_i)\Big)\]

假如我们只研究单变量概率分布之间的变换，那上述过程完全够了。然而，很多真正有意义的事情都是多元的，比如在MNIST上做实验，想要将随机噪声变换成手写数字图像。要注意MNIST的图像是28*28=784像素的，假如每个像素都是随机的，那么这就是一个784元的概率分布。按照我们前面分区间来计算KL距离或者JS距离，哪怕每个像素只分两个区间，那么就有\(2^{784}\approx 10^{236}\)个区间，这是何其巨大的计算量！

为此，我们用神经网络L定义距离：

\[L\Big(\{y_i\}_{i=1}^M, \{z_i\}_{i=1}^N, \Theta\Big)\]

其中，\(\Theta\)为神经网络的参数。

对于特定的任务来说，\(\{z_i\}_{i=1}^N\)是给定的，并非变量，因此上式可简写成：

\[L\Big(\{y_i\}_{i=1}^M, \Theta\Big)\]

通常，我们采用如下的L实现：

\[L=\frac{1}{M}\sum_{i=1}^M D\Big(y_i,\Theta\Big)\]

上式可以简单的理解为：分布之间的距离，等于单个样本的距离的平均。

这里的神经网络\(D(Y,\Theta)\)，实际上就是GAN的另一个主角——鉴别者。这里的D是Discriminator的意思。

如何对抗

因为\(D(Y,\Theta)\)的均值，也就是L，是度量两个分布的差异程度，这就意味着，L要能够将两个分布区分开来，即L越大越好。即：

\[D^* = \arg \max_D V(G,D)\tag{1}\]

但是我们最终的目的，是希望通过均匀分布而生成我们指定的分布，所以\(G(X,\theta)\)则希望两个分布越来越接近，即L越小越好。即：

\[G^* = \arg \min_G \max_D V(G,D)\tag{2}\]

具体的做法是：

Step1

随机初始化\(G(X,\theta)\)，固定它，然后生成一批Y，这时候我们要训练\(D(Y,\Theta)\)，既然L代表的是“与指定样本Z的差异”，那么，如果将指定样本Z代入L，结果应该是越小越好，而将Y代入L，结果应该是越大越好，所以

\[\begin{aligned}\Theta =& \mathop{\arg\min}_{\Theta} L = \mathop{\arg\min}_{\Theta} \frac{1}{N}\sum_{i=1}^N D\Big(z_i,\Theta\Big)\\ \Theta =& \mathop{\arg\max}_{\Theta} L = \mathop{\arg\max}_{\Theta} \frac{1}{M}\sum_{i=1}^M D\Big(y_i,\Theta\Big)\end{aligned}\]

然而有两个目标并不容易平衡，所以干脆都取同样的样本数B（一个batch），然后一起训练就好：

\[\begin{aligned}\Theta =& \mathop{\arg\min}_{\Theta} L_1\\ =&\mathop{\arg\min}_{\Theta} \frac{1}{B}\sum_{i=1}^B\left[D\Big(z_i,\Theta\Big)-D\Big(y_i,\Theta\Big)\right]\end{aligned}\tag{3}\]

公式3的简略推导如下：

\[\ell(\theta)=\log L(\theta)=\sum_{i=1}^my^{(i)}\log h_\theta(x^{(i)})+\sum_{i=1}^m(1-y^{(i)})\log(1-h_\theta(x^{(i)}))\]

上式是二分类的对数似然函数。（参见《机器学习（二）》）具体到这里，可以改写为：

\[E_{x\sim P_{data}}[\log D(x)]+E_{x\sim P_{G}}[\log (1-D(x))]\]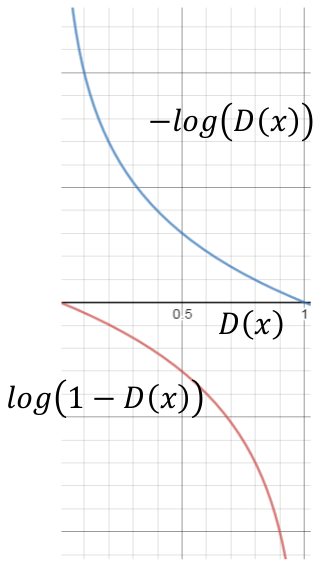

\(\log (1-D(x))\)和\(-\log (D(x))\)的单调性相同，只是下降速度不同。为了迅速收敛，通常采用后者，即：

\[E_{x\sim P_{data}}[\log D(x)]+E_{x\sim P_{G}}[-\log D(x)]\]

为了区分，一般把使用\(\log (1-D(x))\)的GAN称为Minimax GAN，而把使用\(-\log (D(x))\)的GAN称为Non-saturating GAN。

Step2

\(G(X,\theta)\)希望它生成的样本越接近真实样本越好，因此这时候把\(\Theta\)固定，只训练\(\theta\)让L越来越小：

\[\begin{aligned}\theta =& \mathop{\arg\min}_{\theta} L_2\\ =&\mathop{\arg\min}_{\theta} \frac{1}{B}\sum_{i=1}^B\left[D\Big(G(x_i,\theta),\Theta\Big)\right]\end{aligned}\tag{4}\]

从上面的分析，可以看出相对于监督学习，生成模型G的参数更新不是来自于数据样本本身（不是对数据的似然性进行优化），而是来自于判别模型D的一个反传梯度。

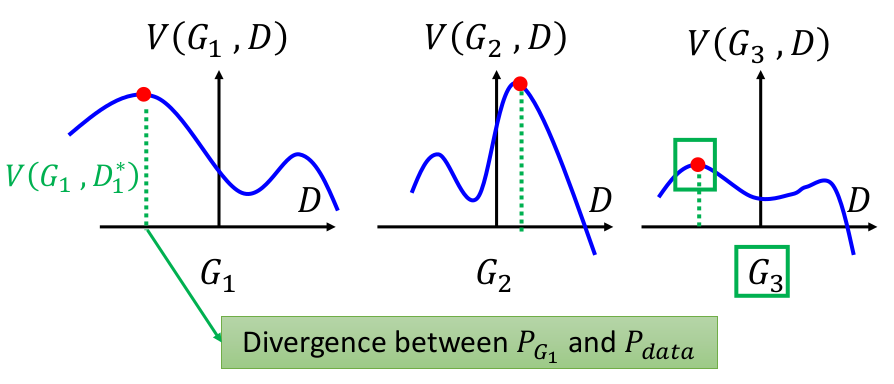
上图展示了GAN的训练步骤：

1.根据Step 1所述，找到3个图中曲线的最高点。

2.根据Step 2所述，选择其中最高点最低的曲线。

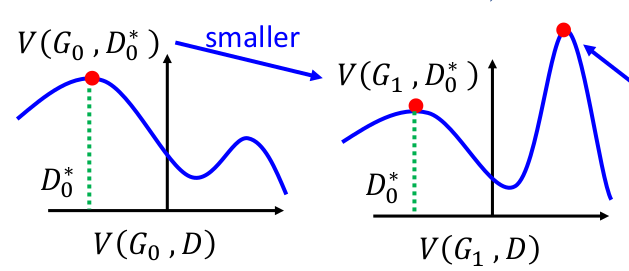
由于\(V(G_0,D_0^*)\)和\(V(G_1,D_0^*)\)的走势不尽相同，前者的下坡有可能是后者的上坡，因此G网络的更新不能太频繁。一般更新D网络k次，更新G网络1次。